Harris Corner Detection

Harris Corner Detection?

Harris Corner Detection이란 말 그대로 Corner를 검출하는 알고리즘 입니다. 디지털 이미지는 pixel들로 이루어져 있는데, 이미지의 특징, 패턴 등을 파악할 때 가장 중요한 point는 corner point 입니다.
따라서, 이러한 corner point를 detection 하는 것은 Computer vision에서 이미지의 특징을 파악할 때 중요한 일 중 하나 입니다.
Harris Corner Detection은 이러한 Corner Detction 알고리즘 중에 가장 기초적이면서 효율적인 알고리즘입니다.

Harris Corner Detection의 원리

Harris Corner Detection의 기본 원리는 Sliding window 방식과 동일합니다.
이미지의 한 픽셀의 중심점으로 잡고, 그 중심 픽셀에 Window를 설정해, Window 내의 픽셀값의 합을 $I(x,y)$로 설정합니다.
그 후 Window를 x축의 방향으로 u만큼, y축의 방향으로 v만큼 이동시켜서 다시 $I(x+u,y+v)$를 구해줍니다.

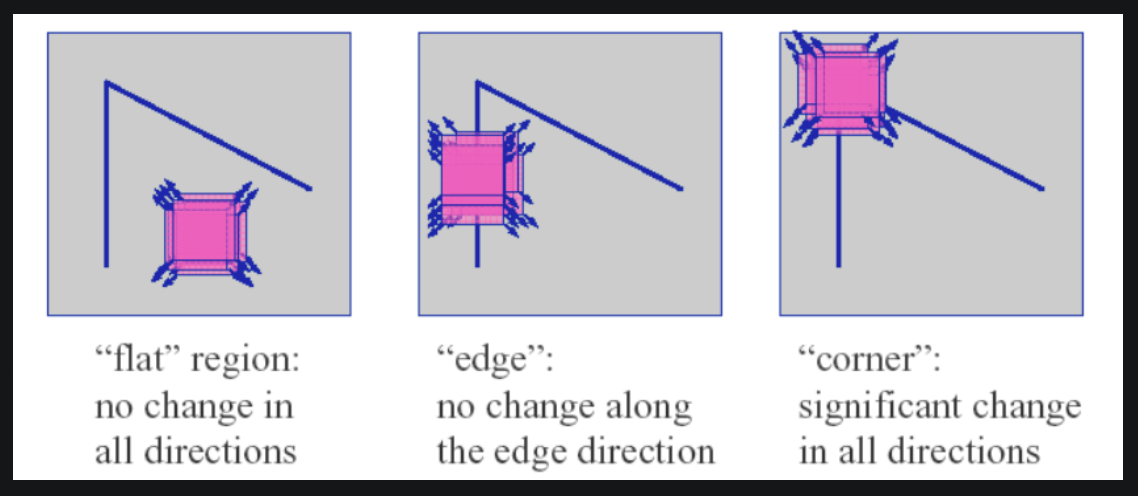
그 때 Window 내의 픽셀 값의 변화는 세가지 형태로 나타납니다.
1. Flat : 픽셀 값이 어느 방향으로든 변화가 없습니다.
2. Edge : 픽셀 값이 한 방향으로만 변화가 있습니다.
3. Corner : 픽셀 값이 모든 방향으로 변화가 있습니다.

Harris corner detection은 위와 같은 성질을 이용해 Corner를 검출합니다.

이제 알고리즘을 자세히 파악해보겠습니다.

먼저, Window가 Sliding하며 변화한 픽셀값을 계산해주어야 합니다.

$E(u,v) = \sum_{(x_k,y_k)\in W}[I(x_k+u,y_k+v) - I(x_k,y_k)]^2$

이와 같이 계산하면, 만약 corner의 경우 $E(u,v)$값이 x축 방향, y축 방향 모두 클 것입니다.

여기서 $I$는 테일러 전개에 의해 다음과 같이 표현할 수 있습니다.

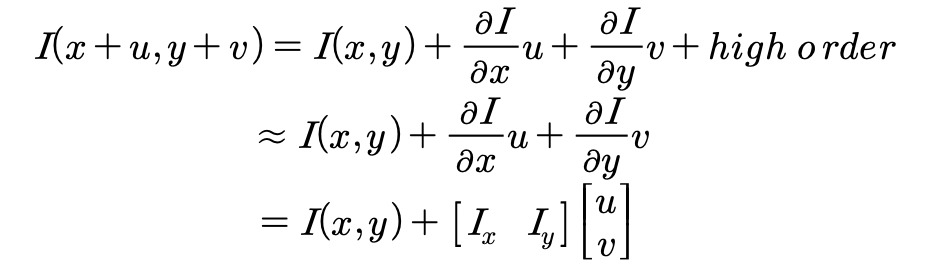
이 식을 다시 $E(u,v)$ 식에 대입하면

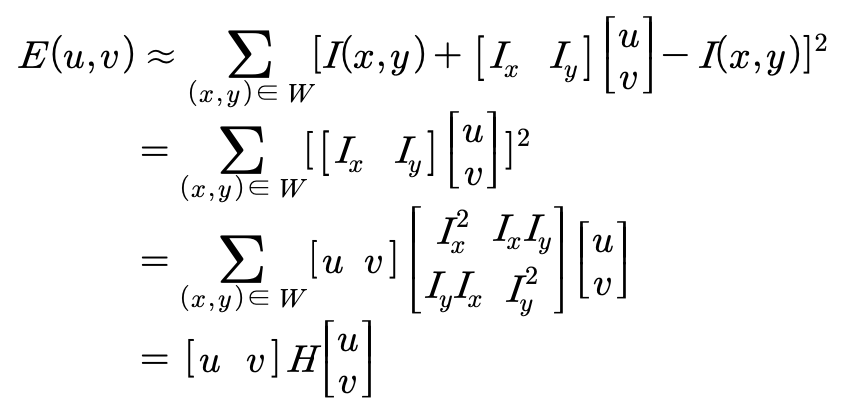
다음과 같이 행렬 곱으로 나타낼 수 있습니다.

이전에 E값이 크면 corner point라고 말했는데, E값이 크기 위해서는 위의 행렬 곱에서 H행렬의 값이 커야합니다.
이제 이 행렬을 고유값 분해하면, x, y축 중에 어느 방향으로 이미지 변화가 큰지 알 수 있을 것 같습니다.
예를 들어, 이 행렬의 eigenvalue값을 $\lambda 1, \lambda 2$로 나타낸다면,

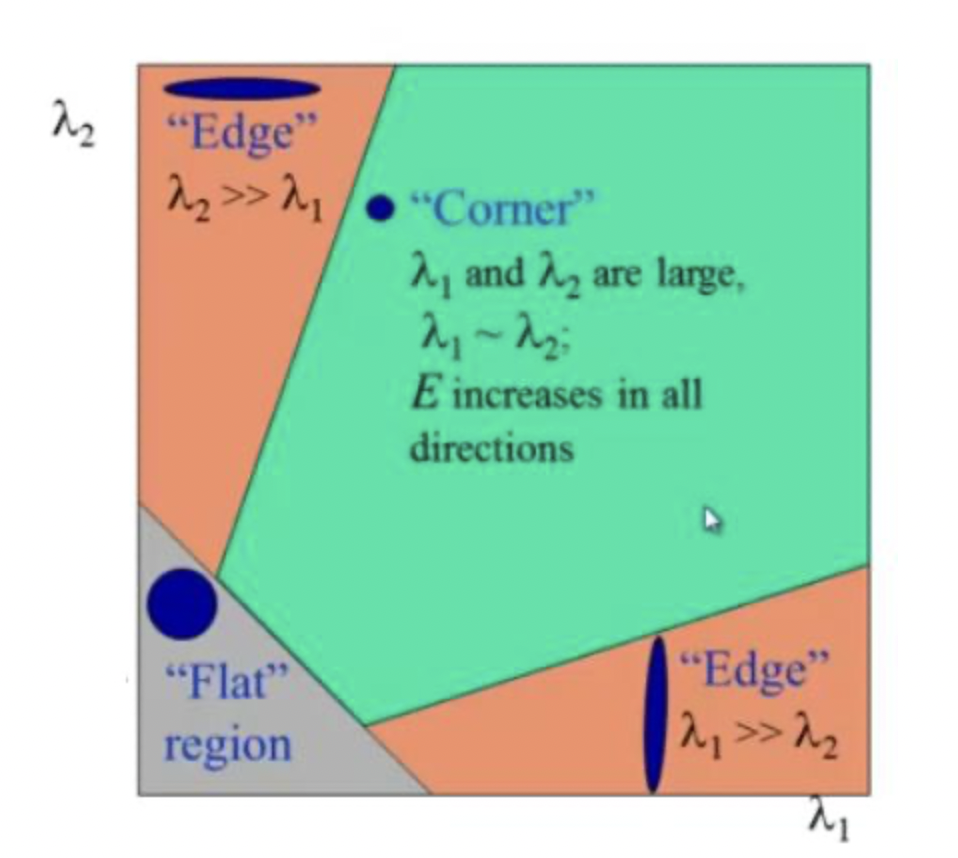
다음과 같이 eigenvalue값의 분포에 따라, edge인지 corner인지 flat인지 판단할 수 있습니다.

하지만 eigenvalue를 직접 계산하는 것은 복잡한 일이기 때문에, 다음과 같은 공식을 이용해 corner인지, edge인지, flat인지를 판단합니다.

$R = det(H) - k(trace(H))^2$

1) $R > 0$ : corner
2) $R < 0$ : edge
3) $R \approx 0$ : flat

이와 같은 판정식에 따라 이미지의 corner, edge, flat을 판단합니다.

Reference

[1] https://bskyvision.com/entry/Harris-코너-검출기의-이해
[2] https://salkuma.files.wordpress.com/2014/04/sifteca095eba6ac.pdf
[3] https://docs.opencv.org/4.x/dc/d0d/tutorial_py_features_harris.html