기초 컴퓨터 비전: (3) Projection & Camera Parameter

고영민·2021년 12월 17일

SLAM: 기초 컴퓨터 비전부터 visual&LiDAR SLAM까지

목록 보기

4/17

1. Basic Projection

앞에서 학습한 homogeneous coordinate를 사용하면 카메라에 상이 투영(projection)되는 현상을 행렬을 이용한 수식으로 모델링이 가능하다. 이렇게 만들어진 모델을 이용하여 우리는 3D 상의 물체가 2D 카메라 영상에 어떻게 투영되는 지, 반대로 어떻게 2D 카메라 영상의 픽셀을 3D 상의 점으로 복원할 수 있는 지 등에 대한 이해가 가능하다.

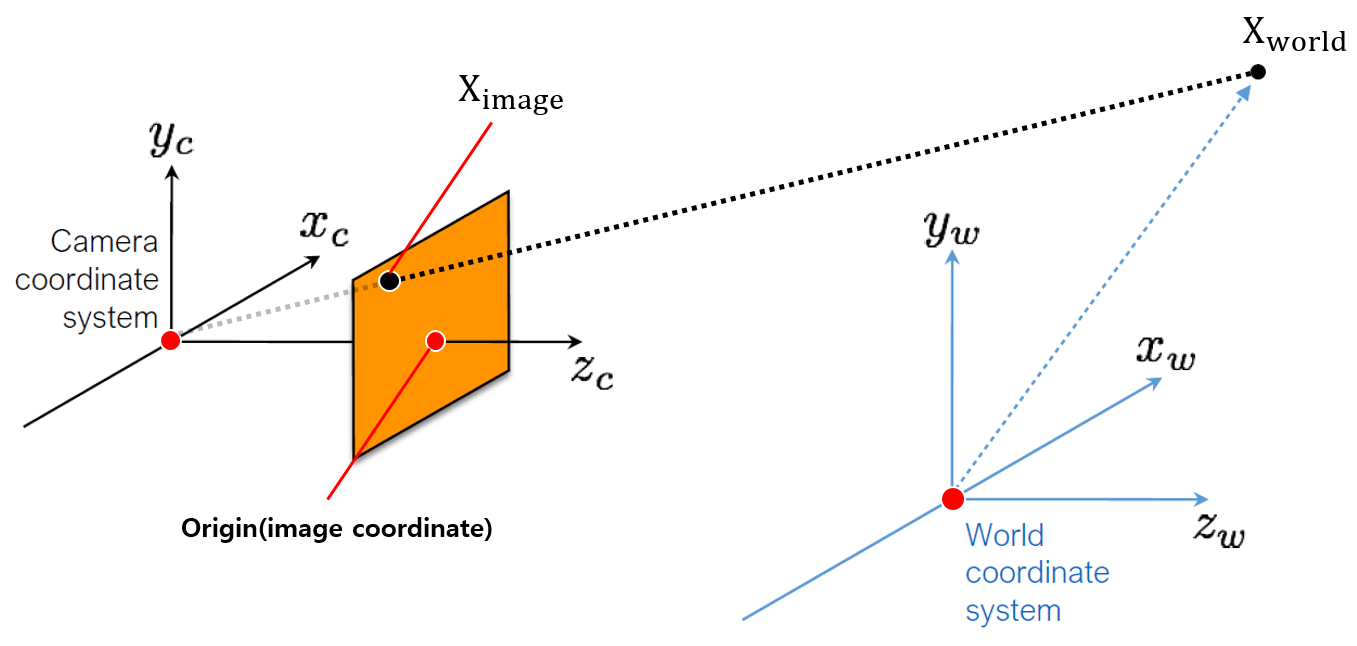
Figure 1. Projection 및 중요 좌표계

우선, 우리가 카메라로 촬영하고 있는 물체의 위치는 $\mathbf{X_{world}}$ 이며, world 좌표계로 표현된다. World 좌표계는 보통 카메라가 움직이더라도 한 곳에 고정되어 있는 것으로 생각하며, 객체 및 SLAM을 통해 작성된 지도 등을 통합하기 위한 기준이 되는 좌표계로 볼 수 있다.

우리의 목적은 카메라에 투영되는 현상을 모델링하는 것이며, 투영은 카메라를 기준으로 기술하는 것이 편하므로, 우선 world 좌표계로 표현된 물체 $\mathbf{X_{world}}$ 를 camera 좌표계 $\mathbf{X_{camera}}$ 로 변환해야한다. 이후 camera 좌표계 $\mathbf{X_{camera}}$ 는 우리의 카메라 모델에 의해 image 좌표계 $\mathbf{X_{image}}$ 로 변환된다.

\mathbf{X_{world}} \rightarrow \mathbf{X_{camera}} \rightarrow \mathbf{X_{image}}

기초적인 projection 모델을 세우기 위하여 다음과 같이 camera 좌표계와 world 좌표계가 일치하고, image 좌표계의 중심이 camera 좌표계의 z축과 일치하는 다음과 같은 환경을 가정해보자.

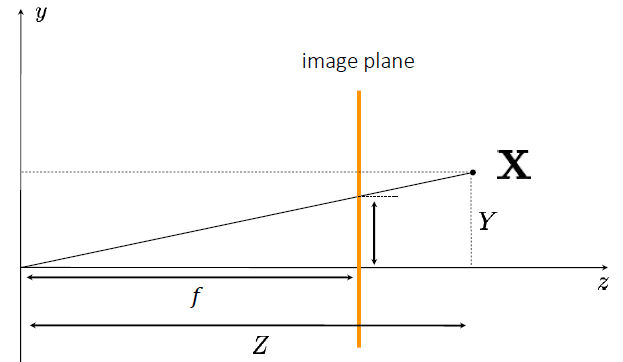
Figure 2. Basic projection

Figure 2에서 $\mathbf{X}=(x,y,z)$ 라고 할 때(camera 좌표계(world 좌표계와 일치)에서 보았을 때), 이를 homogeneous coordinate로 표현하면, $(x,y,z,1)$ 이다. 이러한 $\mathbf{X}$ 가 image plane에 투영되는 좌표(image 좌표계)는 닮음의 성질을 이용하여 쉽게 $(xf/z,yf/z)$ 로 계산될 수 있고, $f=1$ 와 같이 초점거리를 단위길이로 둔다면 image 좌표계에 투영된 좌표는 $(x/z,y/z)$ 며, 이를 homogeneous coordinate로 표현하면, $(x/z,y/z,1) \equiv (x,y,z)$ 이다. 따라서 Figure 2와 같은 기본적인 환경에 대한 투영 모델을 만들기 위해서 $(x,y,z,1) \rightarrow (x,y,z)$ 를 만족하는 행렬을 찾아야 하며, 이는 다음과 같다.

\begin{pmatrix} x\\ y\\ z \end{pmatrix} = \begin{pmatrix} p_1 & p_2 & p_3 & p_4\\ p_5 & p_6 & p_7 & p_8\\ p_9 & p_{10} & p_{11} & p_{12} \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} = [I\mid0] \mathbf{X} = \mathbf{P} \mathbf{X}

따라서 우리는 $\mathbf{X}$ 를 $\mathbf{x} = \mathbf{P} \mathbf{X}$ 와 같이 projection 행렬을 사용하여 3D 상의 물체를 2D image 좌표계로 투영할 수 있으며, 이를 3D를 2D로 투영하는 camera-image transformation으로 볼 수 있다.

2. General Projection & Camera Parameter

위에서 설명된 projection은 매우 간단한 환경에서의 prjection이다. 이를 기반으로 몇 가지 조건을 추가하여 더욱 일반적인 projection 모델을 만들 수 있으며, 그 결과 우리는 더욱 복잡한 형태의 projection 행렬을 얻을 수 있다. 이러한 projection 행렬은 여러개의 파라미터를 포함하고 있으며, 그 파라미터를 camera parameter라고 한다. 카메라의 종류마다 또한 어떻게 촬영하느냐에 촬영된 결과물은 달라지게 되며, camera parameter는 각 카메라의 특성을 나타내는 것으로 볼 수 있다.

2-1. 카메라 내부 파라미터(Camera Intrinsic Parameters)

앞의 기본적인 camera-image transformation에서 우리는 초점거리를 1로 두고, image 좌표계의 중심이 camera 좌표계의 z축 상에 위치한다고 가정하였다. 이러한 가정은 카메라 외적 요소가 아닌 카메라의 내적 요소(카메라가 어떻게 설계되고 만들어졌는지)에 대한 가정으로, 우리는 좀 더 일반적인 내적요소를 가정하여 projection 행렬을 만들 수 있고 그 결과로 생성되는 파라미터를 intrinsic paramete(내부 파라미터)라고 한다.

2-1-1. 임의의 초점거리

임의의 초점거리 $f$ 를 가정한다면, $(x,y,z,1) \rightarrow (xf,yf,z)$ 가 되며, projection 행렬은 다음과 같다.

\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix} = \begin{pmatrix} f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} = \begin{pmatrix} f & 0 & 0\\ 0 & f & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} = \mathbf{K} [I\mid0] \mathbf{X}

2-2-2. 임의의 image 좌표계

앞에서 image 좌표계의 중심이 camera 좌표계의 z축 상에 있다고 가정하였고, 이러한 가정으로 인해 투영된 image 좌표가 닮음의 성질을 이용한 간단한 과정을 통해 계산될 수 있었다. 하지만 현대의 CCD 카메라 등에서는 카메라 센서가 설치된 위치에 따라 image 좌표계의 중심이 camera 좌표계와 일치하지 않을 수 있다.

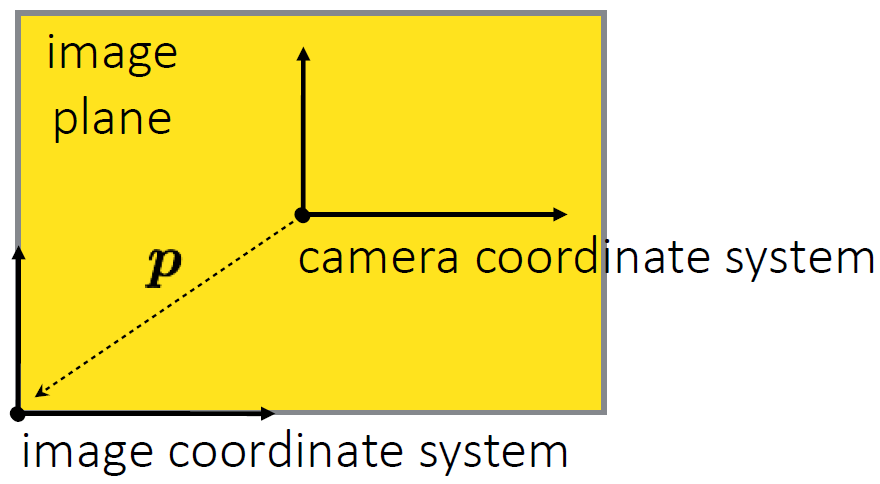
Figure 3. 평행이동된 image 좌표계

Figure 3은 image 좌표계가 평행이동되어 camera 좌표계와 불일치하는 경우이며, image 좌표계가 회전될 수도 있긴 하지만, 보통의 경우 위와 같이 평행이동 정도만 되어 있기 때문에 이 글에서는 이러한 경우만 가정한다.

이러한 image 좌표계의 평행이동은 결국 basic projection의 결과를 image 좌표계가 움직인 $(p_x, p_y)$ 만큼 평행이동 시킨 것과 같다. 따라서 앞선 글에서 설명된 transform 행렬을 참고하여 다음과 같이 정리할 수 있다.

\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix} = \begin{pmatrix} f & 0 & p_x\\ 0 & f & p_y\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} = \mathbf{K} [I\mid0] \mathbf{X}

즉 instrinsic parameter는 camera-image transformation인 $[I\mid0] \mathbf{X}$ 이후에 적용되어, 투영된 image에 대한 변환으로 나타나는 image-image transformation을 구성하는 것으로 볼 수 있다.

2-2-3. 그 외 Intrinsic Parameter 요소

초점거리와 image 좌표의 위치 말고도 다양한 요소들이 intrinsic paramter를 구성할 수 있다. 예를 들어 CCD 카메라의 경우 카메라 센서에 상이 맺히는데, 눈으로 보는 핀홀 카메라와는 달리 CCD 카메라의 센서는 매우 작은 크기의 cell의 집합이다. 따라서 투영된 영상의 결과 또한 discrete한 pixel로 image 좌표를 나타낸다. 따라서 단위 길이당 pixel 수 $m_x, m_y를 적용하여 다음과 같이 표현할 수 있다.

\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix} = \begin{pmatrix} m_x & 0 & 0\\ 0 & m_y & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} f & 0 & p_x\\ 0 & f & p_y\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}\\ = \begin{pmatrix} \alpha_x & 0 & p_x'\\ 0 & \alpha_y & p_y'\\ 0 & 0 & 1 \end{pmatrix}[I\mid0] \mathbf{X}

또한 센서가 skew되어 있을 수도 있는데(skew 변환은 앞선 글 참고) 이는 다음과 같이 $s$ term이 추가된다.

\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix} = \begin{pmatrix} \alpha_x & s & p_x'\\ 0 & \alpha_y & p_y'\\ 0 & 0 & 1 \end{pmatrix}[I\mid0] \mathbf{X}

2-2. 카메라 외부 파라미터(Camera Extrinsic Parameters)

내부 파라미터와는 달리 카메라 외부 파라미터, extrinsic paramters는 카메라 외적인 요소에 대한 파라미터이며, 카메라의 pose와 직접적으로 관련되어 있다. 만약 카메라가 고정되어 있다면, camera 좌표계와 world 좌표계가 일치한다고 가정하여도 큰 문제가 발생하지 않지만, 카메라가 회전하는 등의 변환이 발생한다면 camera 좌표계와 world 좌표계 사이에 차이가 발생한다.

인식된 객체 및 지도 등을 통합하기 위하여 camera 좌표계와 world 좌표계는 구분되어야 한다. Figure 1과 같이 구분된 world 좌표계로 표현된 좌표에 prejection 메트릭스를 적용하기 위해서 world 좌표계로 표현된 좌표를 camera 좌표계로 옮기는 world-camera transform이 필요하며, extrinsic paramters가 그 역할을 한다.

일반적인 경우 카메라 pose에 발생할 수 있는 변환은 회전 및 평행이동 정도이므로, 이 글에서는 이 두 가지 요소만을 가정하며, 앞선 글에서 이러한 변환이 행렬을 통해 표현될 수 있음을 보았다.

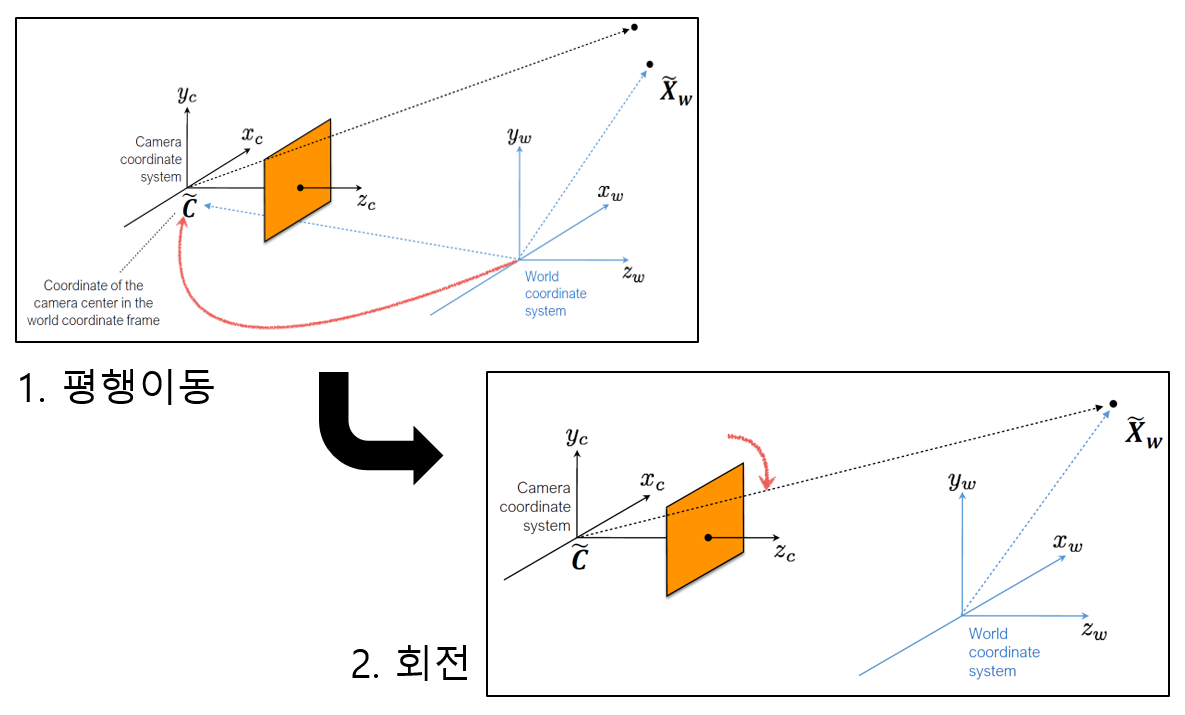
Figure 4. World-camera transform

위와 같이 구분되어있는 camera 좌표계와 world 좌표계 사이의 transform을 찾기 위한 방법으로, 먼저 world 좌표계를 camera 좌표계의 위치로 평행이동하고, 방향을 맞추기 위해 회전시키는 방법을 생각할 수 있다. 이러한 방법은 다음과 같이 표현이 가능하다.