1. 카메라 모델

SLAM 분야는 센서 데이터를 처리하여 로봇의 위치와 자세 추정함과 동시에 지도를 작성하는 분야이다. 이를 위해 사용되는 센서는 매우 다양하며, 이로부터 적절한 정보를 취득하기 위해 각 센서의 원리와 특성을 알아야 한다.

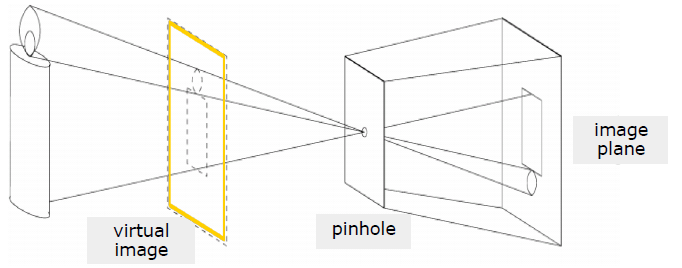
Figure 1. 핀홀 카메라 모델

카메라를 설명하는 가장 기초적인 모델은 핀홀 카메라 모델이다. 핀홀 카메라 모델은 위와 같이 물체에 반사되어 카메라로 들어오는 빛이 작은 구멍을 지나 카메라 내부에 상을 생성하는 것으로, 현대의 카메라에서는 렌즈를 통해 빛을 모으고(작은 구멍) 카메라 센서에 상을 맺히게 하는 것으로 생각할 수 있다.

Visual SLAM에서는 카메라 영상(카메라에 맺힌 상)을 보고 물체의 실제 위치를 알아내어 지도를 작성해야 한다. 따라서 어떤 물체가 카메라 영상에 투영되는 현상을 수식으로 설명할 수 있어야 한다. Figure1에서 실제 상이 맺히는 위치는 카메라 뒷 면에 있는 image plane이지만, 다음 그림과 같이 핀홀을 중심으로 대칭되는 위치에 가상의 image plane을 놓고 그 곳에 투영된다고 생각할 수도 있다.

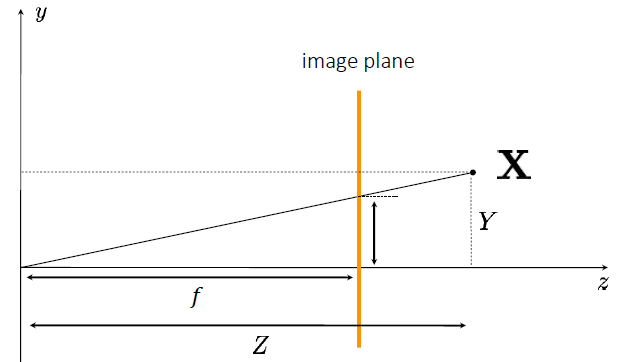
Figure 2. 카메라 좌표계

Figure2는 카메라 좌표계를 나타내며, 카메라는 원점에 위치하고 있고, 이 중심으로 부터 image plane까지의 거리를 초점거리 $f$라고 한다. 이때, 카메라의 중심과 실제 물체의 위치 $\mathbf{X}$를 연결하는 선이 image plane에 닿는 곳에 물체가 투영되며, 우리는 이러한 방식으로 투영되는 것을 행렬을 통해 표현할 수 있다.

Figure2에서 카메라 좌표계 외로 2가지의 좌표계를 더 생각해 볼 수 있다. 첫번째는 카메라가 존재하고 있는 world의 좌표계이며, SLAM에서 카메라는 계속 움직이고 우리는 지도나 로봇 및 카메라의 위치를 나타낼 수 있는 기준이 될 좌표계가 필요하기 때문에 카메라 좌표계와 world 좌표계는 반드시 구분되어야 한다. 두번째는 image 좌표계이며, 일반적으로 image의 픽셀 위치를 나타내는 image plane의 대한 2D 좌표계이다. 기본적인 핀홀 카메라 모델에서는 핀홀을 중심으로 상이 맺히기 때문에 image 좌표계의 중심과 카메라 좌표계의 중심은 같은 선 상에 존재한다. 하지만 현대의 CCD 카메라에서는 카메라 센서가 설치된 위치에 따라 image 좌표계와 카메라 좌표계의 중심은 달라질 수 있다(만약 카메라 센서가 중심에서 약간 평행이동 되어 있다면 맺히는 상의 픽셀 좌표 또한 약간 움직인다).

Figure 3. world 및 image 좌표계

2. Homogeneous Coordinate

Figure2에서 $\mathbf{X}=(x,y,z)$라고 할 때(카메라 좌표계에서 보았을 때), $\mathbf{X}$가 투영되는 좌표는 닮음의 성질을 이용하여 쉽게 $(xf/z,yf/z,f)$로 계산될 수 있다. 만약 초점거리 $f$를 1로 두면 투영된 점의 좌표는 $(x/z,y/z,1)$로 볼 수 있다. 이때 주목해야 하는 점은 $\mathbf{X}$에 어떠한 스칼라값을 곱한 점들도 모두 같은 위치 $(x/z,y/z,1)$로 투영된다는 점이다.

Homogeneous coordinate는 단순히 원래의 좌표에 하나의 차원을 추가함으로써 이러한 성질을 반영하여 어떠한 점을 나타낼 수 있다. 일반적인 Euclidean coordinate의 2차원 점 $(x,y)$를 homogeneous coordinate로 나타내면 3번째 차원을 추가하여 $(x, y, 1)$이 되고, homogeneous coordinate로 표현된 어떤 점 $(x, y, z)$를 Euclidean coordinate의 2차원 점으로 변환하면 $(x/z,y/z)$가 된다.

이러한 성질로 인해 homogeneous coordinate $(x, y, z)$에 임의의 스칼라 $\lambda$를 곱하여도 결국 $(\lambda x, \lambda y, \lambda z) = (\lambda x / \lambda z, \lambda y / \lambda z, \lambda z / \lambda z) = (x/z,y/z,1)$처럼 같은 Euclidean coordinate의 점을 나타내게 되며, 결국 어떤 homogeneous coordinate 점에 스칼라 곱을 하여 얻은 점들도 같은 위치로 투영됨을 의미한다. 따라서 homogeneous coordinate에서는 임의의 스칼라를 곱하여도 서로 같은 것으로 취급한다. 또한 Euclidean coordinate의 3차원 점을 homogeneous coordinate로 나타내는 방법 또한 단순히 4번째 차원을 추가하는 것이다.

Homogeneous coordinate를 사용할 경우의 장점은 다양한 변환을 행렬 계산을 통해 표현할 수 있다는 점이다. 앞선 글에서 회전 변환을 행렬로 표현하였지만, 사실 Euclidean coordinate에서는 몇몇 변환에 대해서 행렬로 표현할 수 없는 경우가 있다.

위의 예시는 점$(x,y)$를 $(t_x, t_y)$만큼 평행이동 시키는 변환이다. 이때, 평행 이동의 경우 실제 환경에서 굉장히 빈번하게 나타나는 변환이지만 Euclidean coordinate에서는 행렬로 표현할 수 없고 homogeneous coordinate을 사용할 경우 위와 같이 행렬을 이용하여 표현할 수 있다.

이 외에도 다음과 같은 변환이 가능하며, SLAM 등에서 우리가 마주할 수 있는 대부분의 변환에 대응이 가능하다.

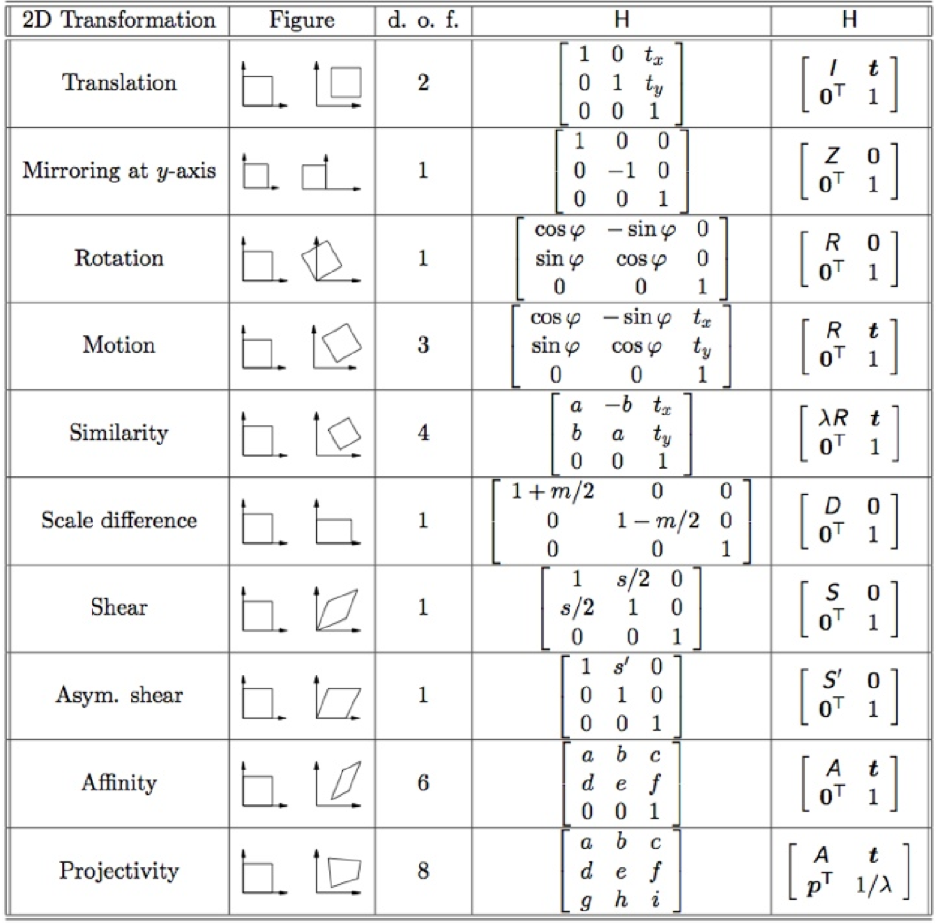
Figure 4. Homogeneous coordinate에서의 변환(2D)

이때, 회전 변환의 경우 3D와 2D 사이에 약간의 차이가 존재한다. 2D의 경우 회전축이 x-y평면에 수직인 축 하나 뿐이지만, 3D의 경우 아래와 같이 3개가 존재한다.

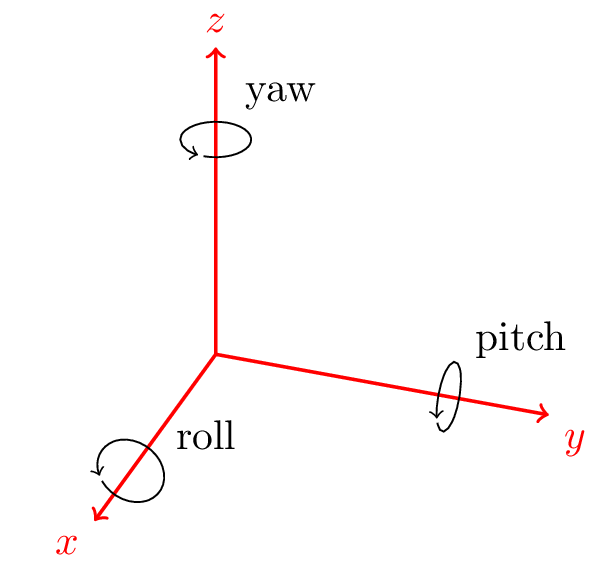
Figure 5. 3D에서의 회전축

따라서 3D에서는 다음과 같이 하나씩 순서대로 회전축을 선택하여 회전 변환 행렬을 만든다.

위의 예시는 x축, y축, z축의 순서로 회전 변환을 수행하는 예시이다(Euclidean coordinate 형태). 이때 주목해야하는 점은 회전 변환 행렬의 최종 형태인 $R^{3D}(\Psi, \phi, \theta)$는 총 9개의 원소를 포함한 행렬이지만, 3개의 미지수($\Psi, \phi, \theta$)에 의해 결정된다는 점이다.

추가적으로 $R_x, R_y, R_z$은 orthogonal matrix이며 각각의 행렬값 또한 1이다. 따라서 그들의 곱인 $R^{3D}$ 또한 orthogonal matrix이고, 행렬값은 1이다. 따라서 $R^{3D}$은 $SO(3)$군에 속한다. (Basic Linear Algebra 6-2 참고)

앞으로 어떤 연산을 하거나 좌표 등을 표현하기 위하여 이러한 homogeneous coordinate는 매우 자주 사용된다. 따라서 homogeneous coordinate에 친숙해지기 위해 다음과 같은 내용을 소개한다.

2-1. Line

2D 좌표에서 일반적으로 직선은 다음과 같은 식으로 나타낼 수 있다.

이때, 점 $(x,y)$를 $(x,y,1)$과 같이 homogeneous coordinate로 나타낼 경우 직선을 다음과 같이 표현 가능하다.

2-2. Intersecting Lines

두 직선의 교점 또한 homogeneous coordinate를 사용할 경우 간단한 형태로 표현할 수 있다. 서로 다른 직선 $\mathbf{l}, \mathbf{m}$이 주어졌을 때, 두 직선 사이에 교점이 존재할 경우 다음과 같이 식을 세울 수 있다.

위의 연립방정식을 Cramer's rule을 사용하여 풀면 다음과 같은 해를 구할 수 있다.

이때, $A_i$는 행렬 $A$의 i번째 행을 $(l_3, m_3)^T$로 바꾼 행렬이다(풀어야 할 연립방정식이 $\mathbf{A}\mathbf{x}=\mathbf{b}$의 형태일 때, A의 i번째 행을 b로 바꿈).

이렇게 계산된 교점을 homogeneous coordinate로 표현하면 다음과 같다.

이 결과는 두 직선의 벡터 $\mathbf{l}, \mathbf{m}$를 외적한 것과 같으며, 따라서 homogeneous coordinate에서 두 직선 $\mathbf{l}, \mathbf{m}$ 사이의 교점은 $\mathbf{x} = \mathbf{l} \times \mathbf{m}$로 나타낼 수 있다.

2-3. Line Between Two Points

두 점을 지나는 직선을 구하는 것 또한 위와 비슷한 방법으로 계산이 가능하다. 서로 다른 두 점 $\mathbf{x}, \mathbf{y}$가 주어졌을 때 두 점을 지나는 직선이 $\mathbf{l}$이라고 하면 다음과 같다.

마찬가지로 Cramer's rule을 적용하면 다음과 같다.

이때, $l_3$를 $l_3\frac{D_3}{D_3}$로 둘 경우, 다음과 같다.

따라서 두 점 $\mathbf{x}, \mathbf{y}$을 지나는 직선은 $\mathbf{l} = \mathbf{x} \times \mathbf{y}$와 같이 표현할 수 있다.

이때, Homogeneous coordinate에서는 점과 직선을 같은 길이의 벡터로 나타낼 수 있고, 두 직선의 교점을 나타내는 식과 두 점을 지나는 선을 나타내는 식이 서로 유사한 것 등 점과 직선 사이에 대칭성(daulity)를 보이고 있음을 알 수 있다.

2-4. Points and Lines at Infinity

Homogeneous coordinate에서는 일반적인 Euclidean coordinate에서는 나타내기 어려운 무한대 점을 다음과 같이 나타낼 수 있다.

Homogeneous coordinate에서 세번째 값을 0으로 둠으로써 무한대를 나타낼 수 있고(Euclidean coordinate로 변환할 때 0으로 나누게 되어 무한대가 됨), $(x,y)$는 해당 무한대 점의 방향을 의미한다.

특히 모든 무한대 점은 위와 같이 $\mathbf{l_{\infty}} = (0,0,1)^T$로 표현되는 무한대 직선 위에 있음을 알 수 있으며, 이러한 무한대 직선을 ideal line이라고 한다.

그리고 Euclidean coordinate에서는 두 평행선이 서로 만나지 않지만, homogeneous coordinate에서는 두 평행선의 교점을 무한대 점을 통해 표현할 수 있다.

Homogeneous coordinate에서 두 평행선 $\mathbf{l}, \mathbf{l'}$을 $(a,b,c), (a,b,c')$와 같이 나타낼 수 있으며, 두 직선의 교점은 다음과 같이 무한대 점으로 나타난다.