기초 컴퓨터 비전: (5) P3P

앞에서 우리는 카메라 캘리브레이션을 통해 카메라 파라미터를 구하였다. 다만 DLT에서는 내/외부 파라미터를 모두 구하였지만, Zhang's method나 타 캘리브레이션 방법들은 많은 경우 내부 파라미터를 구하는 것에 집중한다. 그렇다면 왜곡보정 및 내부 파라미터가 계산된 calibrated camera의 외부 파라미터(포즈)를 어떻게 구할 수 있을까? 여러가지 방법이 있지만, P3P(Projective 3-Point) 알고리즘은 3D 좌표가 알려진 3개의 점을 통해 카메라의 외부 파라미터(포즈)를 추정하는 대표적인 방법이다.

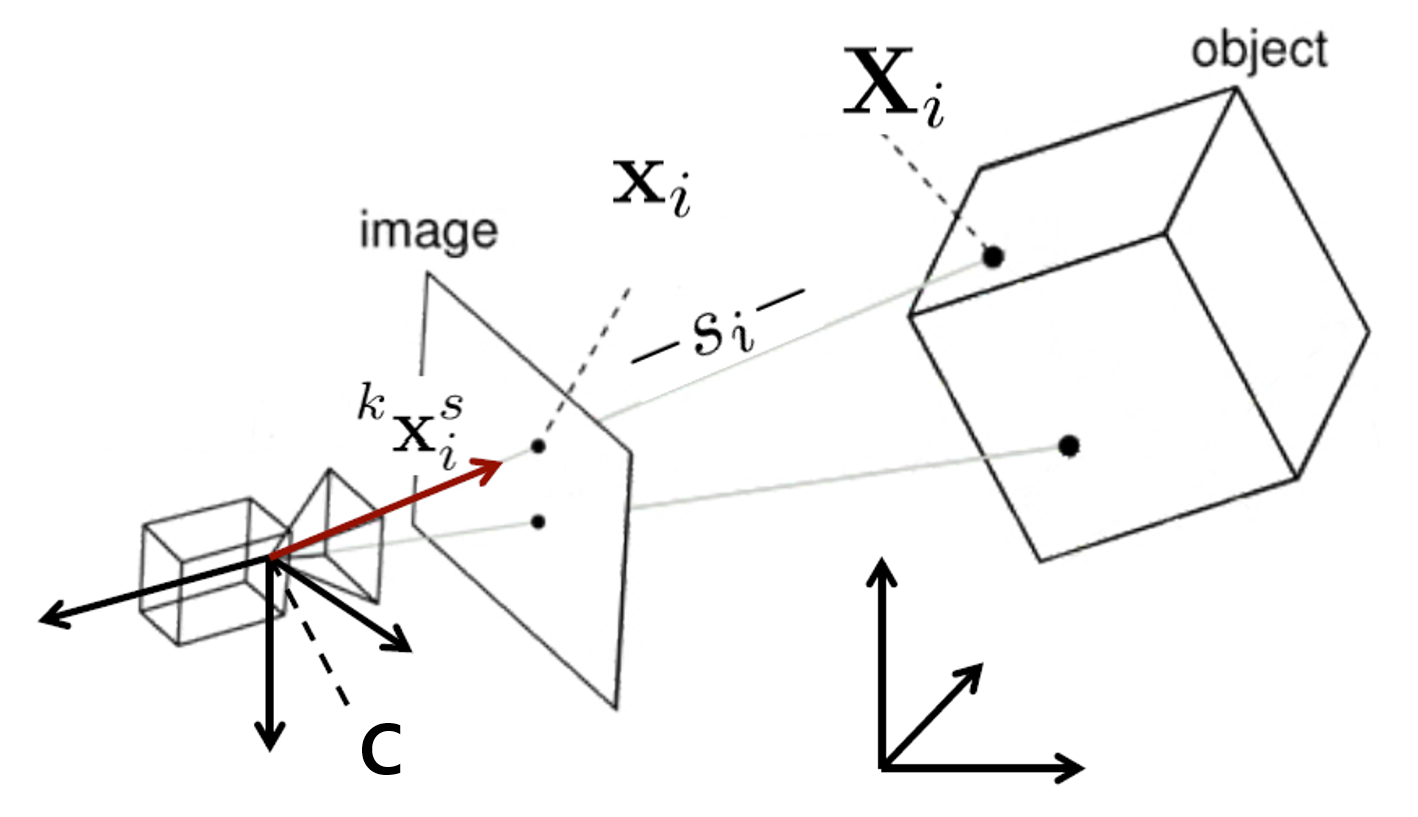
Figure 1. 객체 및 카메라 구성

위 그림에서 객체의 world 좌표 위치 $\mathbf{X_i}$와 카메라좌표 상의 투영 간의 관계는 다음과 같다.

우변은 객체의 world 좌표 위치 $\mathbf{X_i}$를 카메라 좌표로 옮기기 위하여 알맞는 평행이동, 회전을 가한 것이며, 좌변은 카메라 영상에 투영된 위치에 대한 단위 벡터 ${\;}_{}^{k}\mathbf{x_i}^s$에 알맞는 스칼라 값을 곱해 객체와 같은 위치를 가리키게 한 것이다. 이때, 주목할 점은 우리가 이미 카메라의 내부 파라미터는 알고 있다고 가정하였기 때문에 카메라의 초점거리, 중심(principle point) 등을 통해 ${\;}_{}^{k}\mathbf{x_i}^s$는 카메라의 외부 파라미터 없이 알 수 있다는 점이다.

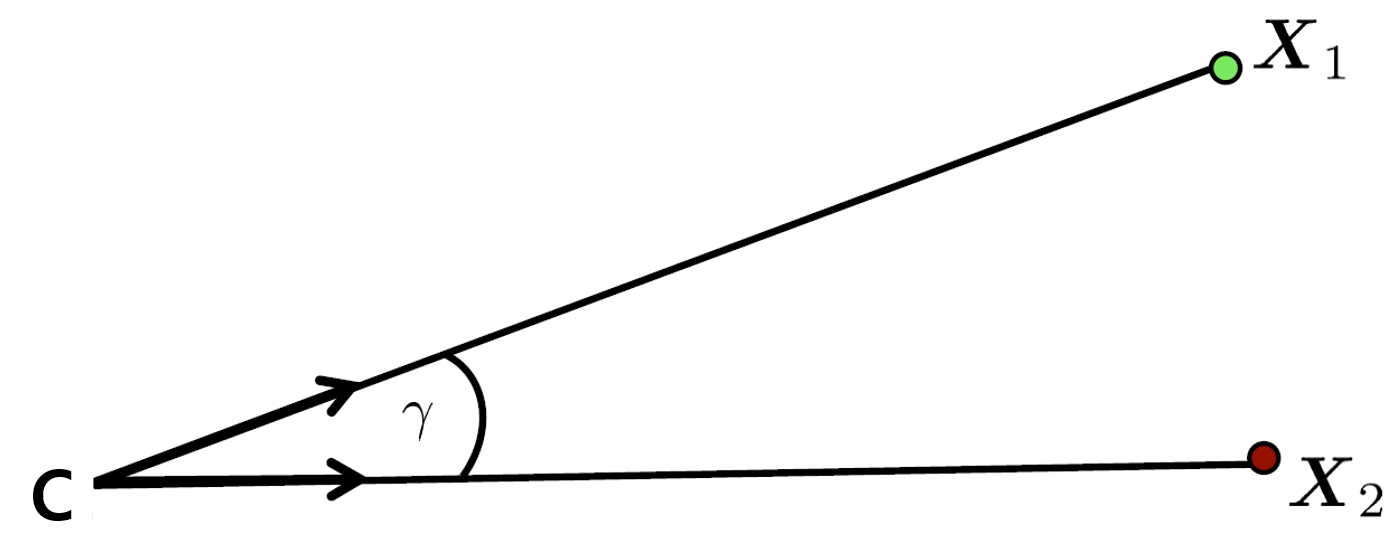
Figure2. 두 점 사이의 각도

이러한 ${\;}_{}^{k}\mathbf{x_i}^s$을 사용하여 위 그림과 같은 상황에서 각도 $\gamma$를 알아 낼 수 있다. 예를 들어 Figure 2에서는 $\overline{C X_1}$의 방향은 ${\;}_{}^{k}\mathbf{x_1}^s$과 같고, $\overline{C X_2}$의 방향은 ${\;}_{}^{k}\mathbf{x_2}^s$와 같다. 따라서 $\cos\gamma={\;}_{}^{k}\mathbf{x_1}^s \cdot {\;}_{}^{k}\mathbf{x_2}^s$이므로 각도 $\gamma$를 알아 낼 수 있다.

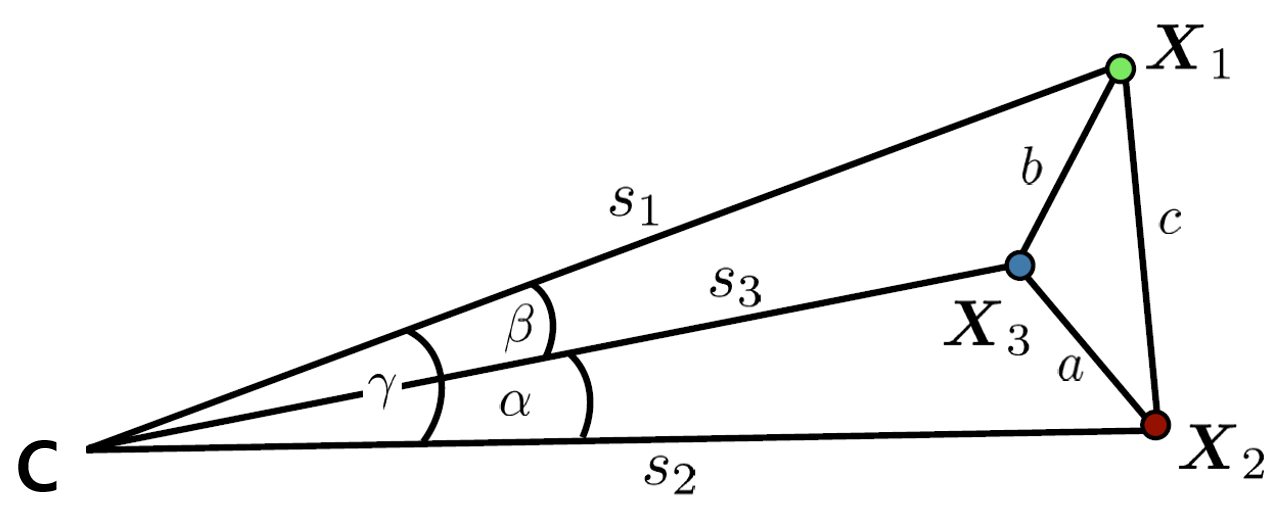
Figure3. 3개의 점이 주어졌을 때

그렇다면 위와 같이 3개의 점이 주어졌을 때 제2코사인 법칙을 사용하여 다음과 같은 식을 만들 수 있다.

여기서 $u=s_2/s_1, \; v=s_3/s_1$으로 두면 다음과 같이 정리할 수 있다.

위의 식을 정리하면 $A_4 v^4 + A_3 v^3 + A_2 v^2 + A_1 v + A_0 =0$와 같이 $v$에 대한 4차 식으로 정리할 수 있다. 각 계수들은 다음과 같으며, 이는 위의 식을 활용하여 직접 전개해보면 알 수 있다.

위의 4차 방정식을 풀어 $v$를 구한 후, $s_1, s_2, s_3$를 구할 수 있는데, 4차 방정식의 해는 최대 4종류 나올 수 있으므로 $s_1, s_2, s_3$ 또한 4종류가 나온다. 이러한 문제를 해결하기 위하여 GPS등의 센서를 이용하여 대략적인 해를 사용하거나 4번째 점을 추가하여 유일한 해를 찾게 된다.

이제 3개 점에 대한 깊이 정보 $s_1, s_2, s_3$를 취득하였으며, 3D-2D 간 투영식인 $s_{i} {\;}_{}^{k}\mathbf{x_i}^s = \mathbf{R}(\mathbf{X_i}-\mathbf{C})$에 대입하여 우리가 필요로 하는 $\mathbf{R}, \mathbf{C}$를 구할 수 있다.

만약 주어진 점이 3개보다 많다면 RANSAC 등의 방법을 통해 더욱 좋은 해를 찾을 수도 있다.