앞선 글에서 카메라 파라미터를 정의하였으며, 이를 통해 3D 상에 있는 객체를 카메라 영상인 2D에 매핑할 수 있었다. 하지만 이러한 연산을 하려면 각 파라미터의 수치를 알아내어야 하는데 그 방법을 카메라 캘리브레이션(calibration)이라고 한다. 캘리브레이션 방법에는 여러가지가 있지만 여기서는 다음의 두가지 방법을 알아본다.

1. DLT (Direct Linear Transform)

3D 상에 있는 객체를 2D 카메라 영상에 매핑하는 식은 다음과 같았다.

카메라 캘리브레이션의 목표는 $\mathbf{K}$ (5 parameter), $\mathbf{R}$ (3 parameter), $\mathbf{C}$ (3 parameter) 등의 내부 또는 외부 등의 파라미터를 찾아내는 것이며, 보통 위와 같이 11개의 파라미터를 결정한다 (사실 굳이 각 파라미터를 구할 필요가 없고 매핑 자체에만 관심이 있다면 $\mathbf{P}$만 구해도 되며 이 경우 풀이가 더 간결해질 수 있다.).

DLT(Direct Linear Transform)을 사용하는 방법에서는 위와 같이 매핑 식을 하나의 행렬 $\mathbf{P}$로 두어 DLT를 통해 행렬 $\mathbf{P}$를 구하고 이로 부터 각 카메라 파라미터를 찾는다. 행렬 $\mathbf{P}$를 이용하면 다음과 같이 적을 수 있다.

위의 식은 homogeneous coodinate로 쓰여진 식이며, 다음과 같이 정리할 수 있다.

이때, 다음과 같이 $\mathbf{a_{x_i}^T}, \mathbf{a_{y_i}^T}$을 사용하면, 각각의 식을 행렬 $\mathbf{P}$의 원소들로 생성한 벡터 $\mathbf{p}$와의 곱으로 표현할 수 있다.

여기서 우리는 하나의 점을 매핑함으로써 2개의 식을 얻을 수 있음을 보았으며, 얻고자 하는 파라미터는 11개이므로 최소한 6개의 점을 사용하여 식을 모아야한다. 이 과정을 통해 여러개의 $\mathbf{a_{x_i}^T}, \mathbf{a_{y_i}^T}$를 모을 수 있으며, 이 벡터들을 쌓아서 하나의 행렬을 만듦으로써 여러개의 점을 하나의 식으로 표현이 가능하다 (다만 모든 $Z_i$가 0이 되는 것과 같이 선택한 모든 점이 한 평면 위에 있다면 행렬 $\mathbf{M}$의 랭크가 줄어 적합한 식이 세워지지 않는다).

이제 위의 식을 풀어 $\mathbf{p}$를 구해야 하는데 행렬 $\mathbf{M}$은 점들의 3D/2D 위치를 기반으로 구성되어 있으므로 당연히 어느정도의 노이즈를 포함하고 있다. 따라서 대부분의 경우 $\mathbf{M}\mathbf{p} = 0$를 정확히 만족하는 $\mathbf{p}$를 구할 수 없으며, $|\mathbf{M}\mathbf{p}|$를 최소로하는 $\mathbf{p}$를 찾는 최소제곱법을 풀게되며, 앞선 글에서 보았듯이 그 해는 $\mathbf{M}$의 가장 작은 특이값에 대응되는 오른쪽 특이벡터이다.

이러한 방법으로 행렬 $\mathbf{P}$를 구하였으며, 이제 행렬 $\mathbf{P}$로부터 파라미터 $\mathbf{K}$,$\mathbf{R}$,$\mathbf{C}$를 복원해야 한다.

이때, $\mathbf{K}$는 삼각행렬, $\mathbf{R}$은 회전변환행렬로써 정규직교한다. $\mathbf{H}^{-1}=\mathbf{R}^{-1}\mathbf{K}^{-1}=$(정규직교행렬)(삼각행렬)이며, 따라서 $\mathbf{H}^{-1}$를 QR decomposition하여 $\mathbf{K}$,$\mathbf{R}$를 구할 수 있다. 이때, 이들은 homogenous이므로 $\mathbf{K}$를 $K_{33}$로 나누어 nomalize할 수도 있다. 카메라 중심 $\mathbf{C}$는 $-\mathbf{H}^{-1}\mathbf{h}$로 구할 수 있다.

2. Zhang's Method

Zhang's method 또한 calibration을 위한 방법 중에 하나이며, 아래와 같은 checker board를 사용하는 방식이다. Checker board는 아래와 같이 특징점을 찾기 쉬운 패턴으로 되어 있으며, 각 격자 간의 거리는 사전에 정의되어 있기 때문에 특징점의 3d 좌표를 알아낼 수 있다(world 좌표의 원점이 checker board의 코너 쪽에 위치해있다고 가정하는 등).

Figure 1. Calibration board

이때, 추출된 모든 점이 한 평면 위에 위치하므로 $Z=0$으로 두어 다음과 같이 매핑식을 간소화 할 수 있다.

이때, $\mathbf{H}$는 8 DoF를 갖고, DLT와 비슷한 방식으로 최소 4개의 점(점 하나당 두 개의 식이 나옴)을 이용하여 $\mathbf{H}$를 구할 수 있다(SVD).

하지만 위에서 일부 원소가 생략($r_{13}, r_{23}, r_{33}$)되었으므로 더이상 $r_{ij}$들이 회전행렬을 이룬다고 할 수 없으며, QR decomposition은 적용할 수 없다. 따라서 위의 식이 만족해야만 하는 두 가지 제약조건을 통해 다른 방법을 적용하여 내부파라미터 $\mathbf{K}$를 찾는다.

위의 식에서 $(\mathbf{r_1},\mathbf{r_2},\mathbf{t})=\mathbf{K}^{-1}(\mathbf{h_1},\mathbf{h_2},\mathbf{h_3})$이고, 따라서 $\mathbf{r_1}=\mathbf{K}^{-1}\mathbf{h_1}, \mathbf{r_2}=\mathbf{K}^{-1}\mathbf{h_2}$이다. 이때, $\mathbf{r_1},\mathbf{r_2}$가 orthonormal 하다는 점에서 다음의 두가지 제약조건이 발생한다.

$|\mathbf{A}\mathbf{x}|=\mathbf{A}\mathbf{x} \cdot \mathbf{A}\mathbf{x}=(\mathbf{A}\mathbf{x})^T\mathbf{A}\mathbf{x}=\mathbf{x}^T\mathbf{A}^T\mathbf{A}\mathbf{x}$에서 norm을 나타내는 표현과 dot product가 있을때 행렬에 transpose가 붙음을 알 수 있다. 따라서 위 제약조건은 다음과 같다.

여기서 우리가 구하고자 하는 $\mathbf{K}$로 이루어진 $\mathbf{K}^{-T}\mathbf{K}^{-1}$를 $\mathbf{B}$로 두자. 이때, $\mathbf{K}^{-T}\mathbf{K}^{-1}$는 양의 정부호 행렬이다(대칭행렬(transpose와 원래 행렬의 곱)이고, $\mathbf{h_1}^T\mathbf{K}^{-T}\mathbf{K}^{-1}\mathbf{h_1}=\mathbf{h_1}^T\mathbf{B}\mathbf{h_1}=|\mathbf{r_1}|$에서 볼 수 있듯이 norm을 의미하는 식이 되어 $\mathbf{h_1} \ne 0$라면 항상 양수). 또한 $\mathbf{K}$가 상삼각행렬이므로, $\mathbf{K}^{-T},\mathbf{K}^{-1}$ 또한 상삼각행렬이고, 따라서 $\mathbf{B}$에 Cholesky decomposition를 적용하여 $\mathbf{K}$를 구할 수 있다.

다만, 아직 행렬 $\mathbf{B}$는 unknown이므로 위 제약조건을 적용하여 행렬 $\mathbf{B}$의 원소들을 구해야한다. Unknown인 행렬 $\mathbf{B}$의 원소들을 모아 벡터 $\mathbf{b}=(b_{11}, b_{12}, b_{13}, b_{22}, b_{23}, b_{33})$을 구성할 수 있다. 여기서 unknown이 6개 뿐인 이유는 행렬 $\mathbf{B}$가 대칭행렬이기 때문이다. 이제 벡터 $\mathbf{v_{ij}}$를 다음과 같이 정의해보자.

이때, 첫번째 제약조건 $\mathbf{h_1}^T\mathbf{K}^{-T}\mathbf{K}^{-1}\mathbf{h_2}=0$은 $\mathbf{v_{12}^T}\mathbf{b}=0$으로, 두번째 제약조건 $\mathbf{h_1}^T\mathbf{K}^{-T}\mathbf{K}^{-1}\mathbf{h_1}-\mathbf{h_2}^T\mathbf{K}^{-T}\mathbf{K}^{-1}\mathbf{h_2}=0$은 $\mathbf{v_{11}^T}\mathbf{b}-\mathbf{v_{22}^T}\mathbf{b}=0$로 쓸 수 있다(이는 제약조건 식들을 직접 전개해보면 알 수 있음).

따라서 하나의 이미지로부터 다음과 같은 식을 세울 수 있으며, 6개의 미지수를 구하기 위해 최소 3장의 이미지를 촬영해 식을 세우고 DLT에서 사용한 SVD를 통해 행렬 $\mathbf{B}$를 구할 수 있다.

3. Distortion

앞에서 우리들은 카메라 파라미터를 이용하여 3D 상의 점을 2D의 카메라 영상으로 매핑할 수 있었다. 하지만 실제 카메라를 보면 이러한 파라미터로 계산된 위치 $(x, y)$와는 다른 위치에 매핑이 되는데, 이는 카메라 파라미터를 행렬을 통해 곱하는 것처럼 linear한 방식으로 나타낼 수 없는 non-linear한 요소가 존재하기 때문이다. 이러한 요소에는 여러가지가 있지만, 가장 대표적인 것은 렌즈에 의한 왜곡(distortion)이며, 아래와 같이 렌즈 가장자리에서 영상이 휘어지는 등의 왜곡이 있다.

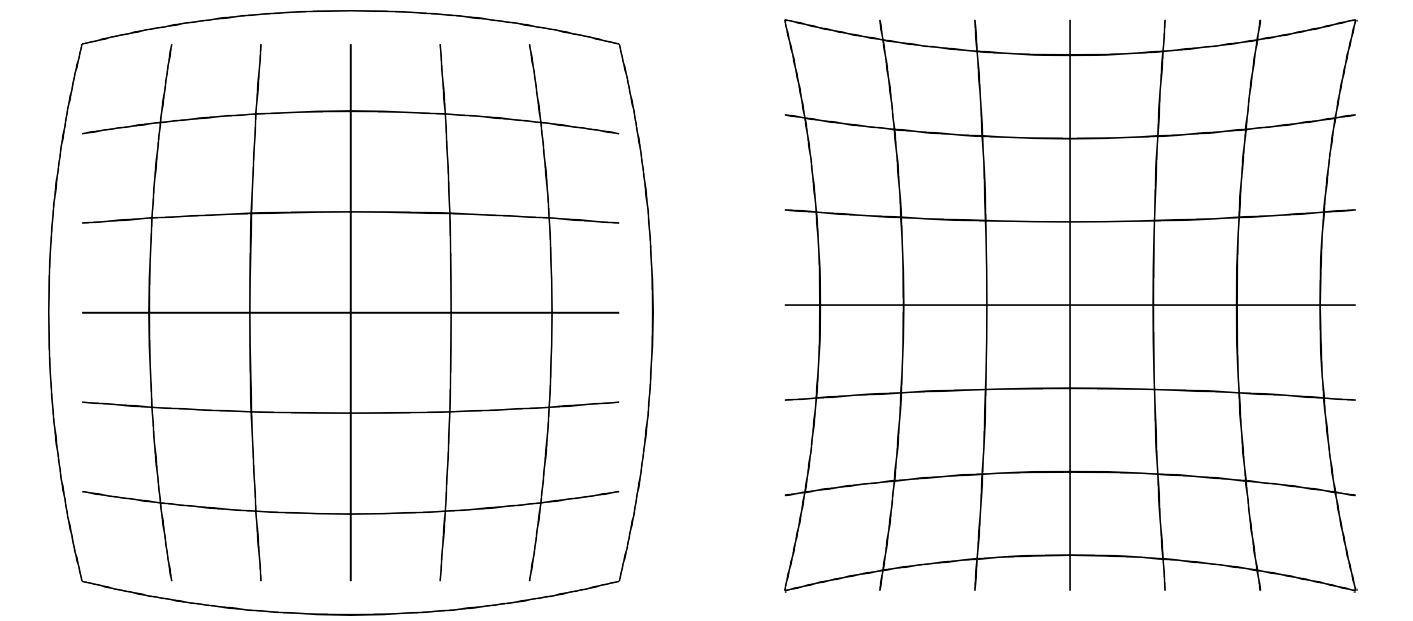
Figure 2. 렌즈 왜곡

이러한 왜곡을 모델링하는 방법 또한 여러가지가 있지만, 대표적인 방법으로는 다음과 같은 barrel distortion 모델이 있다.

여기서 사용된 non-linear parameter인 $q_1, q_2$를 구하여 왜곡을 제거할 수도 있으며, 이를 구하기 위해 실제 촬영된 영상에서 나타난 점의 위치와 위 왜곡모델로 계산된 점의 위치 사이의 차이를 최소화 하는 최소제곱법이 사용된다. 다만 이를 풀기 위해서는 Levenberg-Marquardt 방법 등의 non-linear 최적화 방법이 사용되어야 한다.