1. 문제

출처: 백준 25682번 체스판 다시 칠하기 2

2. 풀이

백준 1018번 체스판 다시 칠하기 풀이는 주어진 보드의 크기가 작았기 때문에, for문을 4개나 돌리는 방식으로 구현해도 가능하였다.

이번 문제의 경우에는 판이 커졌기 때문에 같은 방식으로 구현하면 당연히 시간 초과가 발생한다.
따라서 판이 체스판의 형태와 얼마나 다르게 생겼는지 DP 방식으로 접근하여 계산하고, 체스판을 잘라서 비교하는 형태로 풀어야 한다.

위의 설명과 같이 주어진 판의 해당 위치까지 체스판과 얼마나 다른 부분들이 있는지 개수를 저장하는 DP 2차원 리스트를 만든다.

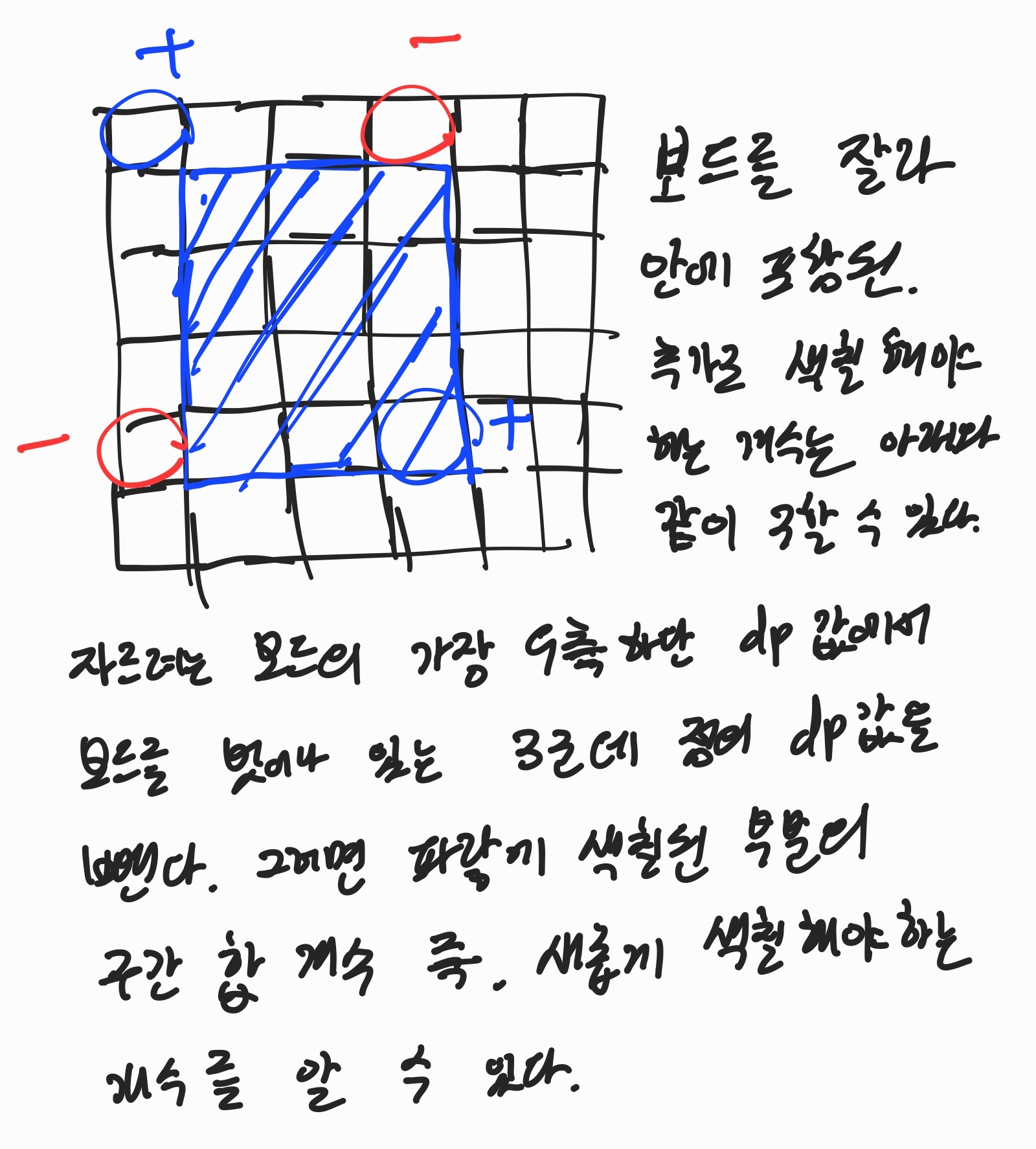
위의 설명과 같이 구간합을 구하는 방식을 사용하여, 자른 체스판 안에 다시 칠해야 하는 부분의 개수가 얼마인지 계산할 수 있다.

체스판의 형태가 "B, W, B", "W, B, W" 두 가지 형태가 가능하므로, 두 경우에 대해서 가장 작은 개수를 구한 후 최종적인 값을 출력하면 된다.

이렇게 접근하여도, 시간 초과가 발생할 수 있으므로 PyPy3을 써야 한다.

3. 소스코드

import sys
input = sys.stdin.readline

N,M,K = map(int,input().split())
board = [list(input()) for _ in range(N)]

def min_board(color):
    dp = [[0]*(M+1) for _ in range(N+1)]
    for i in range(N):
        for j in range(M):
            if (i+j)%2 == 0:
                temp = board[i][j] != color
            else:
                temp = board[i][j] == color
            dp[i+1][j+1] = dp[i][j+1] + dp[i+1][j] - dp[i][j] + temp
    
    count = K*K
    for i in range(1,N-K+2):
        for j in range(1,M-K+2):
            count = min(count,dp[i+K-1][j+K-1] - dp[i-1][j+K-1] - dp[i+K-1][j-1] + dp[i-1][j-1])
    return count

print(min(min_board('B'), min_board('W')))

4. 그 외

체스판 칠하기 1 때보다 훨씬 복잡해졌다. 처음 문제를 접하였을 때에는, BW인 경우와 WB인 경우를 어떻게 계산해야 하나 답답했었다. 다른 분의 풀이를 보고 함수 형태로 구현하면 되는구나를 깨달았을 때는 여전히 함수로 생각하는 건 미숙하구나 싶었다.