목적
EfficientNet을 이해하고 Pytorch로 구현할 수 있다.
Architecture
- Network architecture
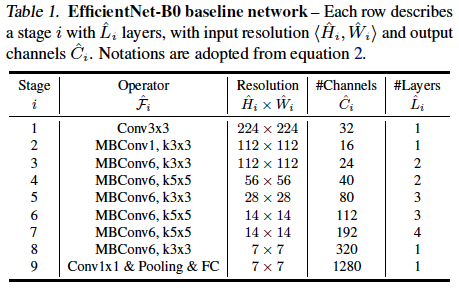
여러 EfficientNet시리즈의 기본이 되는EfficientNet-B0의 구조이다. 이 구조를 바탕으로 depth, width, resolution을 조절하면서Efficient-B1~EfficientNet-B7까지 구현한다.MBConv:MobileNet-v3에서 사용된 Inverted bottleneck 구조를 뜻한다.
ex)MBConv6, k3x36은depthwiselayer 이전Conv에서 채널수를 몇 배 키울 것인지를 결정한다.k3x3은depthwiselayer의Conv의kernel size를 나타낸다.Resolution: 해당 layer에input으로 들어갈H x W크기이다.#Channels: 해당 layer의output_channels#Layers: 해당 layer를 몇 번 반복해서 쌓을지
어떻게 depth, width, resolution을 조절하는지는 아래에서 설명.
특징
"On-device에서 좋은 성능을 보이는 모델을 만들어 보자" 라는 MobileNet의 지향점과는 다르게 EfficientNet은 다시 ResNet, SE-Net 등 처럼 모델의 크기에 제한을 두지 않으며 좋은 성능을 보이는 모델을 만드는 것을 지향하였음.
- Compound scaling
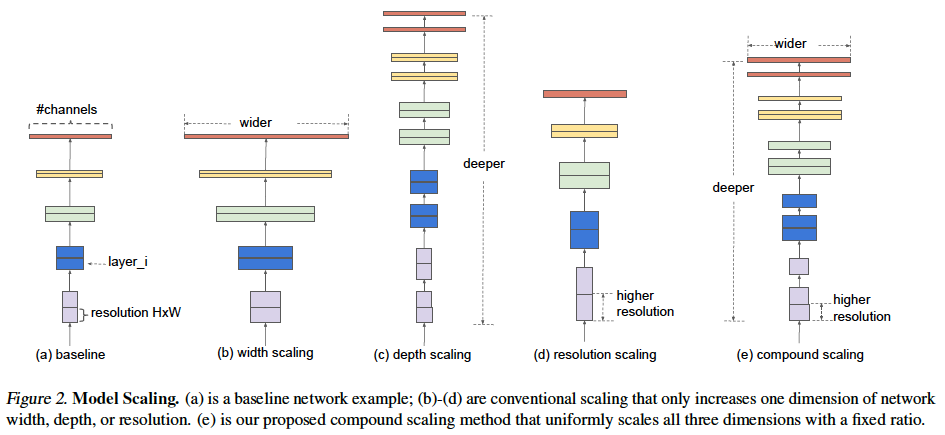
그 동안 Width scaling 연구도 해보았고(WideResNet), Depth scaling(ResNet), Resolution (MobileNet)에 대해서도 연구해보았다.
EfficientNet은 이 세가지 요소 (width, depth, resolution)를 종합해서 늘려보자는 것이다. (Compound Scaling)
- 다른 factor들을 고정하고 Width, Depth, Resolution을 각각 scaling up 했을 때의 성능 비교
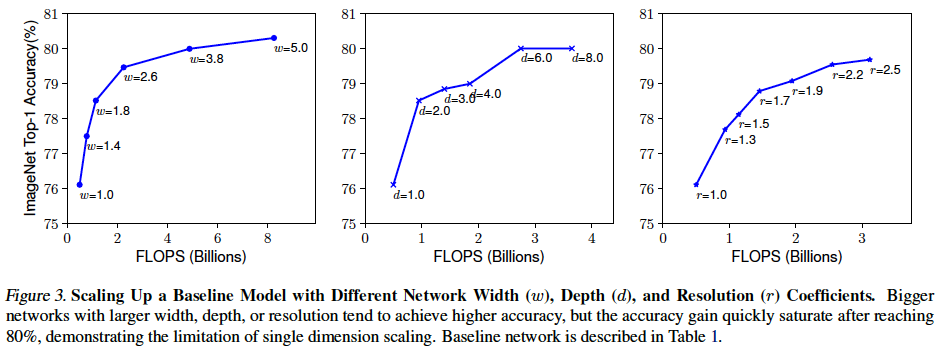
- 키우면 키울수록 성능이 좋아지지만 모두 Top-1 Accuracy 기준 약 80 ~ 81% 의 정도의 성능에서 saturation 되는 현상을 볼 수 있다.
- 특히 depth에 대한 scaling up 그래프를 보면 다른 factor들 보다 더 saturation이 빨리 되는 것을 확인할 수 있다.
- Width, Depth, Resolution의 밸런스를 조절해 Scaling Up을 한 성능
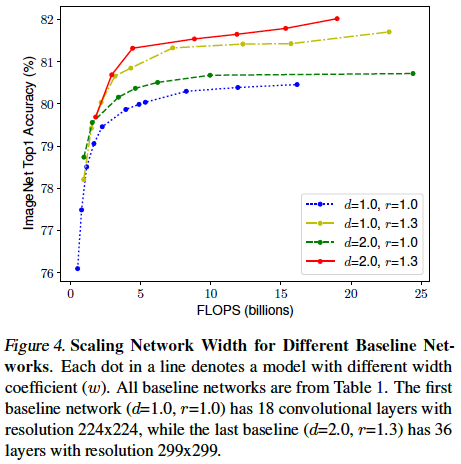
- 예상대로 여러 factor들을 키우면 키울수록 좋다는 것을 볼 수 있다.
- 하지만 이 그래프에서 중점적으로 봐야할 부분은 같은 연산량(
FLOPS)에서도 조합에 따라 성능이 많게는 1 % 이상 달라진다는 것을 확인할 수 있다. - 즉, width, depth, resolution을 "밸런스를 맞추어 조화롭게" 키우는 것이 중요하다.
- 어떤 기준으로 밸런스를 조절?
width, depth, resolution 이 세 가지를 조화롭게 키우는게 중요하는 것은 알겠다. 그래서 어떻게 밸런스를 맞출건데?
depth를 , width를 , resolution을 로 놓고 만 키우는 방식으로 컨트롤 할 것이다.
연산량을 기준으로 생각해보자.
width를 2 배 키운다면? 모델 연산량은 4 배 증가
depth를 2 배 키운다면? 모델 연산량은 2 배 증가
resolution를 2 배 키운다면? 모델 연산량은 4 배 증가
즉, depth, width, resolution 각각을 , , 배 만큼 키웠을 때의 증가되는 연산량은 배 이다.
이 논문에서는 증가되는 연산량의 배수를 "2"로 기준을 세워 아래와 같은 식을 세웠다.
EfficientNet은 이 식에서 를 바꾸어 가며 , , 값을 적용해 depth, width, resolution을 조절하였다.
ex) = 0EfficientNet-B0
다양한 값을 사용해EfficientNet을B0에서B7까지 제안했다.
(실제 구현에서는 값이 자연수가 아닌 경우도 있기 때문에 값이EfficientNet시리즈 넘버와 꼭 같지만은 않다.)
그리고 , , 값은 각각1.2,1,1,1,15이다. 이 값은 어떻게 결정 되었을까?
논문에서는 위 식에서 로 놓고 GridSearch 방식으로 , , 를 결정했다고 한다.
가장 accuracy를 크게하는 , , 값을 선정
결과
- 모델 성능 비교
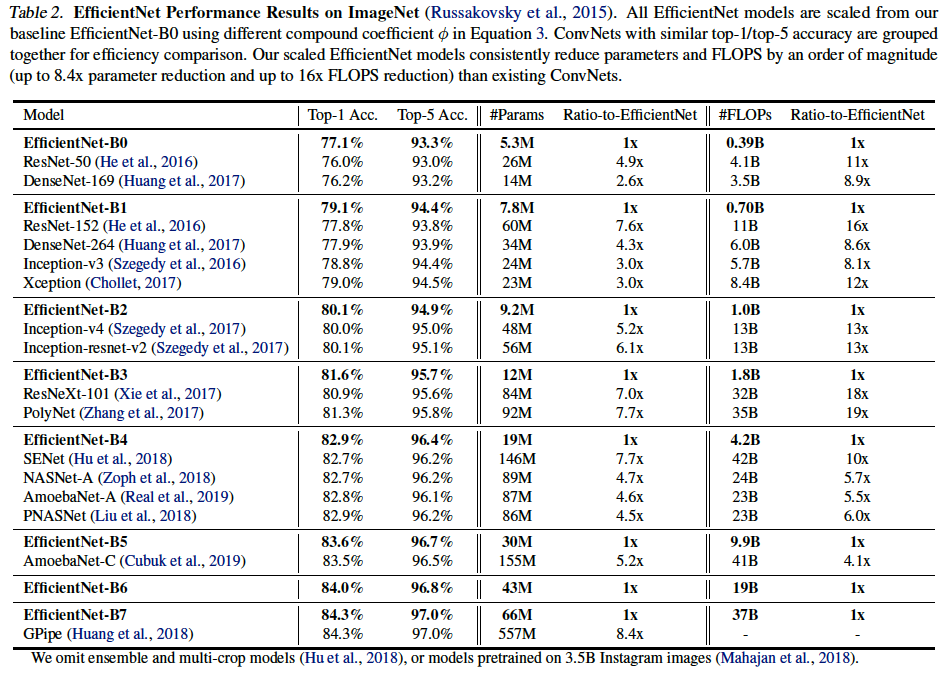비슷한 성능을 내는 모델들 사이에서 파라미터 수(#Params)로 보나 연산량(#FLOPs)로 보나 어마어마한 효율을 가진다. 바꾸어 말하면EfficientNet은 비슷한 파라미터수와 연산량을 갖는 다른 모델을 비교해보면 성능 차이가 엄청나다. 한 가지 예로EfficientNet-B4와ResNet-50을 비교해보자.EfficientNet-B4의 파라미터 수가 더 적고, 연산량은 비슷하지만 Top1-Acc 기준ResNet-50보다 약 7 % 정도 성능이 높은 것을 볼 수 있다.
- 다른 모델과 비교
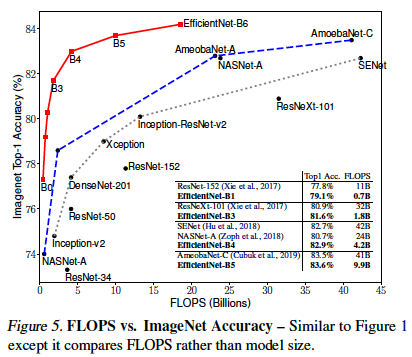다른 여러 모델들에 비해 적은 연산량으로도 월등히 높은 성능을 가진다는 것을 볼 수 있다.
- CAM 분석
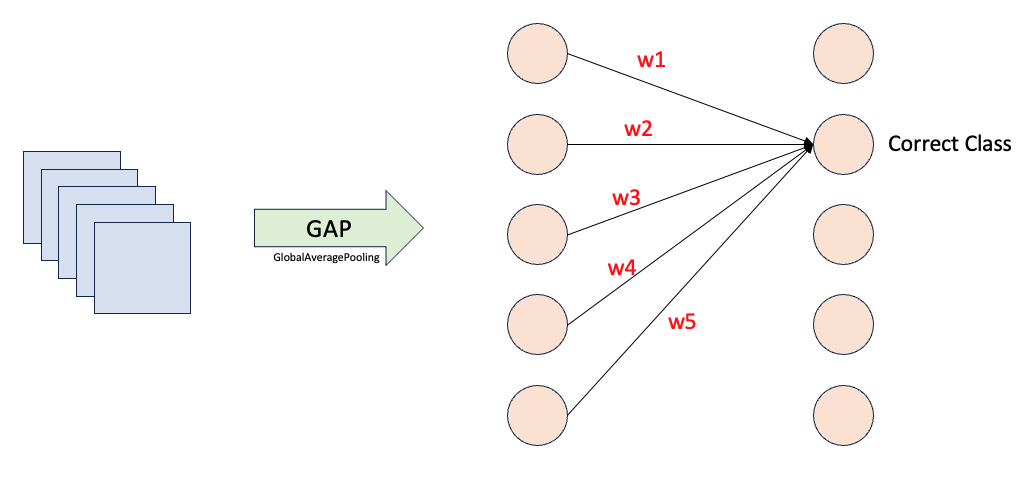
CAM은 Class Activation Map의 약자이다. CAM을 통해 모델이 해당 클래스를 예측함에 있어 이미지의 어떤 부분을 가장 많이 보았는지 (고려했는지) 알 수 있다. 계산자체는 간단하다. GAP 이후 target하는 class을 예측하는데 기여한 weight들을 각각 GAP 바로 이전 feature map들에 weighted sum 한다. 끝이다. 이후 원본 이미지를 GAP 이전 feature map와 같은 사이즈로 resize해서 비교해서 보면 된다.
GAP 바로 이전의 feature map들은 이미 여러 Conv를 통과함으로써 넓은 receiptive field를 갖고 매우 정제된 정보를 포함한다. 그리고 GAP로 인해 feature map에 대한 정보는 하나의 값으로 응축될 텐데 그 정보들을 사이에서도 해당 class를 결정하기 위해 더 중요하게 봐야하는 정보는 당연히 더 높은 weight 값을 가질 것이다. 따라서 해당 클래스를 결정하는데 사용된 각각의 weight값을 GAP 바로 이전 feature map들에 각각 곱하고 모두 더해 (weighted sum) 시각화 하여 살펴보면 해당 클래스를 결정하는데 있어 어떤 부분을 중요하게 보고 결정했는지를 알 수 있다.
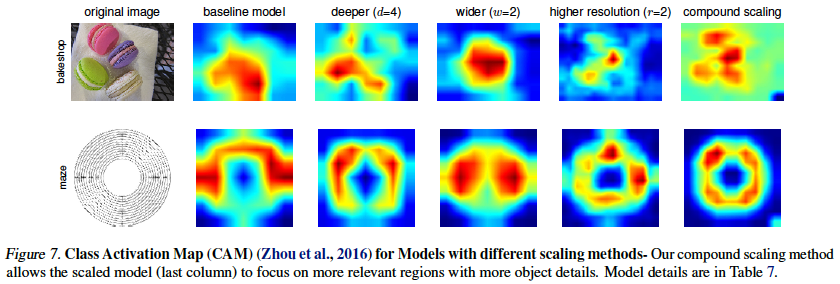compound scaling 모델은 다른 모델들에 비해 타겟하는 물체를 더 중점적으로 보고 예측했다는 것을 확인할 수 있다.
- EfficientNet-B0을 각각 Scaling 한 결과와 Compound Scaling 한 결과 비교
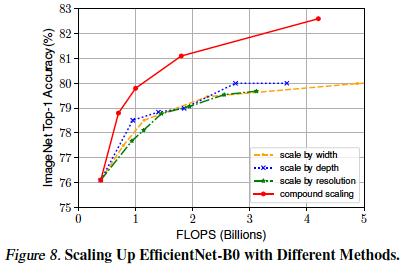depth, width, resolution을 각각 scaling up 하는 것 보다 compound scaling up이 훨씬 더 좋다는 것을 한 번 더 확인할 수 있다.
Code
환경
- python 3.8.16
- pytorch 2.1.0
- torchinfo 1.8.0
- pandas 2.0.3
- torchvision 0.16.0
구현
import math
import pandas as pd
import torch
from torch import nn
from torchvision import transforms
from torchvision.ops import StochasticDepth
from torchinfo import summarydef _make_divisible(v, divisor, min_value = None):
"""
This func is taken from the original tensorflow repo.
In ensures that all layers have a channel number that is divisibale by 8
It can be seen here:
https://github.com/tensorflow/models/blob/master/research/slim/nets/mobilenet/mobilenet.py
"""
if min_value is None:
min_value = divisor
new_v = max(min_value, int(v + divisor / 2) // divisor * divisor)
# Make sure that round down does not go down by more than 10%.
if new_v < 0.9 * v:
new_v += divisor
return int(new_v)class SE_Block(nn.Module):
def __init__(self, in_channels, squeeze_channels):
super().__init__()
self.squeeze = nn.AdaptiveAvgPool2d((1, 1))
self.excitation = nn.Sequential(
nn.Linear(in_channels, squeeze_channels),
nn.SiLU(inplace = True),
nn.Linear(squeeze_channels, in_channels),
nn.Sigmoid()
)
def forward(self, x):
se = self.squeeze(x)
se = torch.flatten(se, 1)
se = self.excitation(se)
se = se.unsqueeze(dim = 2).unsqueeze(dim = 3)
out = se * x
return out
class MBConv(nn.Module):
def __init__(self, kernel_size, in_channels, exp_channels, out_channels, stride, sd_prob):
super().__init__()
self.use_skip_connection = (stride == 1 and in_channels == out_channels)
self.stochastic = StochasticDepth(sd_prob, mode = "row")
expand = nn.Sequential(
nn.Conv2d(in_channels, exp_channels, 1, bias = False),
nn.BatchNorm2d(exp_channels, momentum = 0.99),
nn.SiLU(inplace = True),
)
depthwise = nn.Sequential(
nn.Conv2d(exp_channels, exp_channels, kernel_size, stride, padding = (kernel_size - 1) // 2, groups = exp_channels, bias = False),
nn.BatchNorm2d(exp_channels, momentum = 0.99),
nn.SiLU(inplace = True),
)
squeeze_channels = in_channels // 4 # reduction_ratio = 4
se_block = SE_Block(exp_channels, squeeze_channels)
pointwise = nn.Sequential(
nn.Conv2d(exp_channels, out_channels, 1, bias = False),
nn.BatchNorm2d(out_channels, momentum = 0.99),
# No Activation
)
layers = []
if in_channels < exp_channels:
layers += [expand]
layers += [depthwise, se_block, pointwise]
self.residual = nn.Sequential(*layers)
def forward(self, x):
if self.use_skip_connection:
residual = self.residual(x)
residual = self.stochastic(residual)
return residual + x
else:
return self.residual(x)class EfficientNet(nn.Module):
def __init__(self, num_classes, depth_mult, width_mult, resize_size, crop_size, drop_p, stochastic_depth_p = 0.2):
super().__init__()
cfgs = [
#[k, t, c, n, s]
[3, 1, 16, 1, 1],
[3, 6, 24, 2, 2],
[5, 6, 40, 2, 2],
[3, 6, 80, 3, 2],
[5, 6, 112, 3, 1],
[5, 6, 192, 4, 2],
[3, 6, 320, 1, 1],
]
self.transforms = transforms.Compose(
[
transforms.Resize(resize_size, interpolation = transforms.InterpolationMode.BICUBIC),
transforms.CenterCrop(crop_size),
transforms.ToTensor(),
transforms.Normalize(mean = [0.485, 0.456, 0.406], std = [0.229, 0.224, 0.225]),
]
)
in_channels = _make_divisible(32 * width_mult, 8)
# First layer
self.first_conv = nn.Sequential(
nn.Conv2d(3, in_channels, 3, stride = 2, padding = 1, bias = False),
nn.BatchNorm2d(in_channels, momentum = 0.99),
nn.SiLU(inplace = True)
)
# Inverted Residual Blocks
layers = []
num_block = 0
num_total_layers = sum(math.ceil(cfg[-2] * depth_mult) for cfg in cfgs)
for kernel_size, t, c, n, s in cfgs:
n = math.ceil(n * depth_mult)
for i in range(n):
stride = s if i == 0 else 1
exp_channels = _make_divisible(in_channels * t, 8)
out_channels = _make_divisible(c * width_mult, 8)
sd_prob = stochastic_depth_p * (num_block / (num_total_layers - 1))
layers.append(MBConv(kernel_size, in_channels, exp_channels, out_channels, stride, sd_prob))
in_channels = out_channels
num_block += 1
self.layers = nn.Sequential(*layers)
# Last several layers
last_channels = _make_divisible(1280 * width_mult, 8)
self.last_conv = nn.Sequential(
nn.Conv2d(in_channels, last_channels, 1, bias = False),
nn.BatchNorm2d(last_channels, momentum = 0.99),
nn.SiLU(inplace = True)
)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Sequential(
nn.Dropout(p = drop_p),
nn.Linear(last_channels, num_classes),
)
def forward(self, x):
x = self.first_conv(x)
x = self.layers(x)
x = self.last_conv(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.fc(x)
return x# https://github.com/pytorch/vision/blob/main/torchvision/models/efficientnet.py#L439
def efficientnet_b0(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=1.0, width_mult=1.0, resize_size=256, crop_size=224, drop_p=0.2, **kwargs)
def efficientnet_b1(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=1.1, width_mult=1.0, resize_size=256, crop_size=240, drop_p=0.2, **kwargs)
def efficientnet_b2(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=1.2, width_mult=1.1, resize_size=288, crop_size=288, drop_p=0.3, **kwargs)
def efficientnet_b3(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=1.4, width_mult=1.2, resize_size=320, crop_size=300, drop_p=0.3, **kwargs)
def efficientnet_b4(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=1.8, width_mult=1.4, resize_size=384, crop_size=380, drop_p=0.4, **kwargs)
def efficientnet_b5(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=2.2, width_mult=1.6, resize_size=456, crop_size=456, drop_p=0.4, **kwargs)
def efficientnet_b6(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=2.6, width_mult=1.8, resize_size=528, crop_size=528, drop_p=0.5, **kwargs)
def efficientnet_b7(num_classes=1000, **kwargs):
return EfficientNet(num_classes=num_classes, depth_mult=3.1, width_mult=2.0, resize_size=600, crop_size=600, drop_p=0.5, **kwargs)model = efficientnet_b5()
summary(model, input_size=(2,3,456,456), device='cpu')#### OUTPUT ####
====================================================================================================
Layer (type:depth-idx) Output Shape Param #
====================================================================================================
EfficientNet [2, 1000] --
├─Sequential: 1-1 [2, 48, 228, 228] --
│ └─Conv2d: 2-1 [2, 48, 228, 228] 1,296
│ └─BatchNorm2d: 2-2 [2, 48, 228, 228] 96
│ └─SiLU: 2-3 [2, 48, 228, 228] --
├─Sequential: 1-2 [2, 512, 15, 15] --
│ └─MBConv: 2-4 [2, 24, 228, 228] --
│ │ └─Sequential: 3-1 [2, 24, 228, 228] 2,940
│ └─MBConv: 2-5 [2, 24, 228, 228] --
│ │ └─Sequential: 3-2 [2, 24, 228, 228] 1,206
│ │ └─StochasticDepth: 3-3 [2, 24, 228, 228] --
│ └─MBConv: 2-6 [2, 24, 228, 228] --
│ │ └─Sequential: 3-4 [2, 24, 228, 228] 1,206
│ │ └─StochasticDepth: 3-5 [2, 24, 228, 228] --
│ └─MBConv: 2-7 [2, 40, 114, 114] --
│ │ └─Sequential: 3-6 [2, 40, 114, 114] 13,046
│ └─MBConv: 2-8 [2, 40, 114, 114] --
│ │ └─Sequential: 3-7 [2, 40, 114, 114] 27,450
│ │ └─StochasticDepth: 3-8 [2, 40, 114, 114] --
│ └─MBConv: 2-9 [2, 40, 114, 114] --
│ │ └─Sequential: 3-9 [2, 40, 114, 114] 27,450
│ │ └─StochasticDepth: 3-10 [2, 40, 114, 114] --
│ └─MBConv: 2-10 [2, 40, 114, 114] --
│ │ └─Sequential: 3-11 [2, 40, 114, 114] 27,450
│ │ └─StochasticDepth: 3-12 [2, 40, 114, 114] --
│ └─MBConv: 2-11 [2, 40, 114, 114] --
│ │ └─Sequential: 3-13 [2, 40, 114, 114] 27,450
│ │ └─StochasticDepth: 3-14 [2, 40, 114, 114] --
│ └─MBConv: 2-12 [2, 64, 57, 57] --
│ │ └─Sequential: 3-15 [2, 64, 57, 57] 37,098
│ └─MBConv: 2-13 [2, 64, 57, 57] --
│ │ └─Sequential: 3-16 [2, 64, 57, 57] 73,104
│ │ └─StochasticDepth: 3-17 [2, 64, 57, 57] --
│ └─MBConv: 2-14 [2, 64, 57, 57] --
│ │ └─Sequential: 3-18 [2, 64, 57, 57] 73,104
│ │ └─StochasticDepth: 3-19 [2, 64, 57, 57] --
│ └─MBConv: 2-15 [2, 64, 57, 57] --
│ │ └─Sequential: 3-20 [2, 64, 57, 57] 73,104
│ │ └─StochasticDepth: 3-21 [2, 64, 57, 57] --
│ └─MBConv: 2-16 [2, 64, 57, 57] --
│ │ └─Sequential: 3-22 [2, 64, 57, 57] 73,104
│ │ └─StochasticDepth: 3-23 [2, 64, 57, 57] --
│ └─MBConv: 2-17 [2, 128, 29, 29] --
│ │ └─Sequential: 3-24 [2, 128, 29, 29] 91,664
│ └─MBConv: 2-18 [2, 128, 29, 29] --
│ │ └─Sequential: 3-25 [2, 128, 29, 29] 256,800
│ │ └─StochasticDepth: 3-26 [2, 128, 29, 29] --
│ └─MBConv: 2-19 [2, 128, 29, 29] --
│ │ └─Sequential: 3-27 [2, 128, 29, 29] 256,800
│ │ └─StochasticDepth: 3-28 [2, 128, 29, 29] --
│ └─MBConv: 2-20 [2, 128, 29, 29] --
│ │ └─Sequential: 3-29 [2, 128, 29, 29] 256,800
│ │ └─StochasticDepth: 3-30 [2, 128, 29, 29] --
│ └─MBConv: 2-21 [2, 128, 29, 29] --
│ │ └─Sequential: 3-31 [2, 128, 29, 29] 256,800
│ │ └─StochasticDepth: 3-32 [2, 128, 29, 29] --
│ └─MBConv: 2-22 [2, 128, 29, 29] --
│ │ └─Sequential: 3-33 [2, 128, 29, 29] 256,800
│ │ └─StochasticDepth: 3-34 [2, 128, 29, 29] --
│ └─MBConv: 2-23 [2, 128, 29, 29] --
│ │ └─Sequential: 3-35 [2, 128, 29, 29] 256,800
│ │ └─StochasticDepth: 3-36 [2, 128, 29, 29] --
│ └─MBConv: 2-24 [2, 176, 29, 29] --
│ │ └─Sequential: 3-37 [2, 176, 29, 29] 306,048
│ └─MBConv: 2-25 [2, 176, 29, 29] --
│ │ └─Sequential: 3-38 [2, 176, 29, 29] 496,716
│ │ └─StochasticDepth: 3-39 [2, 176, 29, 29] --
│ └─MBConv: 2-26 [2, 176, 29, 29] --
│ │ └─Sequential: 3-40 [2, 176, 29, 29] 496,716
│ │ └─StochasticDepth: 3-41 [2, 176, 29, 29] --
│ └─MBConv: 2-27 [2, 176, 29, 29] --
│ │ └─Sequential: 3-42 [2, 176, 29, 29] 496,716
│ │ └─StochasticDepth: 3-43 [2, 176, 29, 29] --
│ └─MBConv: 2-28 [2, 176, 29, 29] --
│ │ └─Sequential: 3-44 [2, 176, 29, 29] 496,716
│ │ └─StochasticDepth: 3-45 [2, 176, 29, 29] --
│ └─MBConv: 2-29 [2, 176, 29, 29] --
│ │ └─Sequential: 3-46 [2, 176, 29, 29] 496,716
│ │ └─StochasticDepth: 3-47 [2, 176, 29, 29] --
│ └─MBConv: 2-30 [2, 176, 29, 29] --
│ │ └─Sequential: 3-48 [2, 176, 29, 29] 496,716
│ │ └─StochasticDepth: 3-49 [2, 176, 29, 29] --
│ └─MBConv: 2-31 [2, 304, 15, 15] --
│ │ └─Sequential: 3-50 [2, 304, 15, 15] 632,140
│ └─MBConv: 2-32 [2, 304, 15, 15] --
│ │ └─Sequential: 3-51 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-52 [2, 304, 15, 15] --
│ └─MBConv: 2-33 [2, 304, 15, 15] --
│ │ └─Sequential: 3-53 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-54 [2, 304, 15, 15] --
│ └─MBConv: 2-34 [2, 304, 15, 15] --
│ │ └─Sequential: 3-55 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-56 [2, 304, 15, 15] --
│ └─MBConv: 2-35 [2, 304, 15, 15] --
│ │ └─Sequential: 3-57 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-58 [2, 304, 15, 15] --
│ └─MBConv: 2-36 [2, 304, 15, 15] --
│ │ └─Sequential: 3-59 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-60 [2, 304, 15, 15] --
│ └─MBConv: 2-37 [2, 304, 15, 15] --
│ │ └─Sequential: 3-61 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-62 [2, 304, 15, 15] --
│ └─MBConv: 2-38 [2, 304, 15, 15] --
│ │ └─Sequential: 3-63 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-64 [2, 304, 15, 15] --
│ └─MBConv: 2-39 [2, 304, 15, 15] --
│ │ └─Sequential: 3-65 [2, 304, 15, 15] 1,441,644
│ │ └─StochasticDepth: 3-66 [2, 304, 15, 15] --
│ └─MBConv: 2-40 [2, 512, 15, 15] --
│ │ └─Sequential: 3-67 [2, 512, 15, 15] 1,792,268
│ └─MBConv: 2-41 [2, 512, 15, 15] --
│ │ └─Sequential: 3-68 [2, 512, 15, 15] 3,976,320
│ │ └─StochasticDepth: 3-69 [2, 512, 15, 15] --
│ └─MBConv: 2-42 [2, 512, 15, 15] --
│ │ └─Sequential: 3-70 [2, 512, 15, 15] 3,976,320
│ │ └─StochasticDepth: 3-71 [2, 512, 15, 15] --
├─Sequential: 1-3 [2, 2048, 15, 15] --
│ └─Conv2d: 2-43 [2, 2048, 15, 15] 1,048,576
│ └─BatchNorm2d: 2-44 [2, 2048, 15, 15] 4,096
│ └─SiLU: 2-45 [2, 2048, 15, 15] --
├─AdaptiveAvgPool2d: 1-4 [2, 2048, 1, 1] --
├─Sequential: 1-5 [2, 1000] --
│ └─Dropout: 2-46 [2, 2048] --
│ └─Linear: 2-47 [2, 1000] 2,049,000
====================================================================================================
Total params: 30,389,784
Trainable params: 30,389,784
Non-trainable params: 0
Total mult-adds (G): 20.53
====================================================================================================
Input size (MB): 4.99
Forward/backward pass size (MB): 3162.78
Params size (MB): 121.56
Estimated Total Size (MB): 3289.33
====================================================================================================