[논문리뷰] Image Inpainting for Irregular Holes Using Partial Convolutions

1. Introduction

Image inpainting는 위와 같이 이미지의 hole 부분을 자연스럽고 그럴듯하게 채워넣는 것이다. 이 논문에서는 Irregular한 구멍들을 Partial Convolution을 이용해 Image inpainting하는 방법을 제안한다.

(a)와 같은 이미지를 여러 기법으로 inpainting 했을 때의 결과를 보여준다. 평균값으로 채우거나 (e, f) 여러 다른 기법을 사용한 것 (b, c, d) 보다 논문에서 제안하는 Partial Conv를 이용했을 때 더 inpainting을 잘 했다는 것을 보여준다.

2. Approach

이 논문에서 처음으로 제안하는 Partial Conv와 이를 쌓아서 만든 Model architecture, Loss function을 소개해보자 한다.

2-1. Partial Convolutional layer

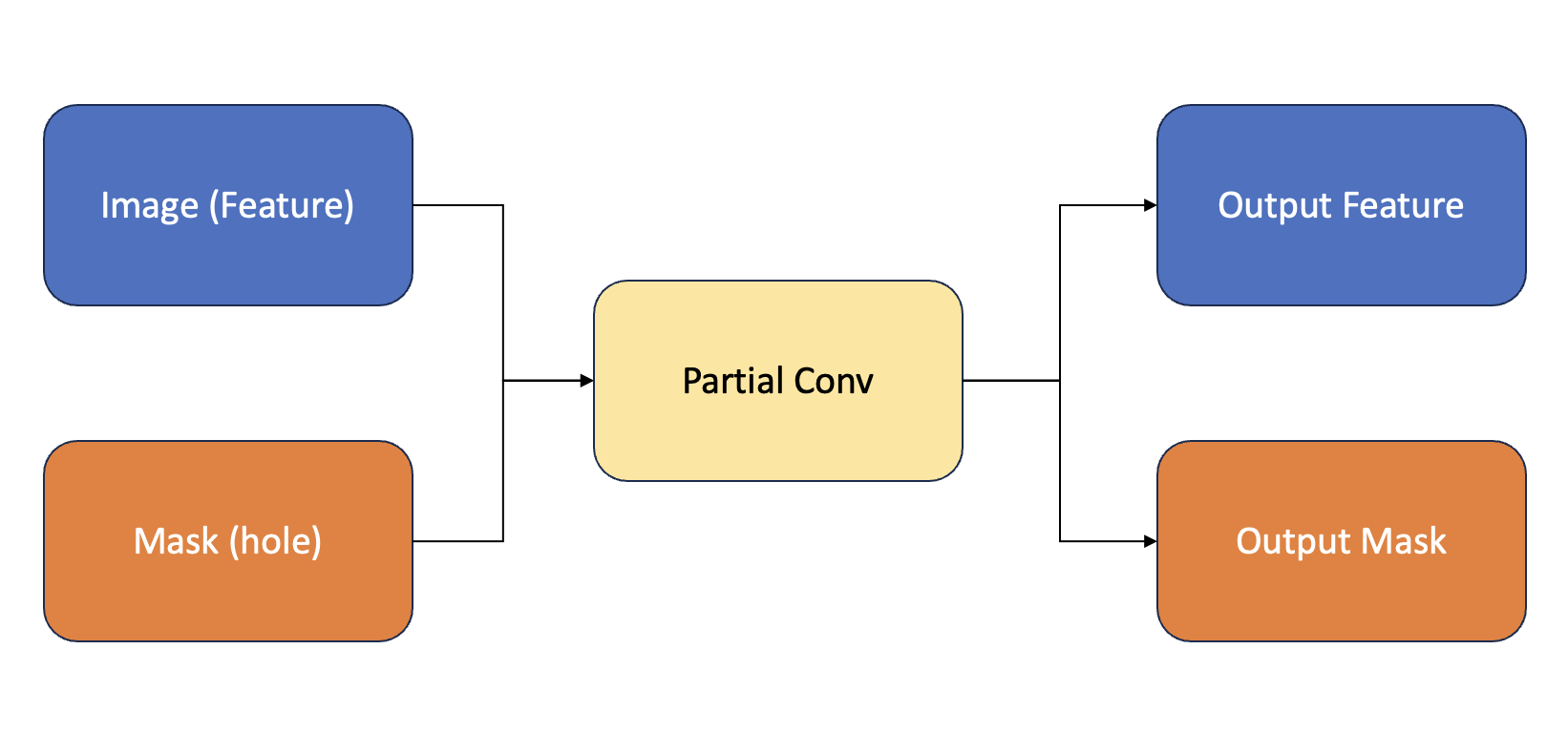
Partial Convolutional layer는 input으로 Image(feature)와 mask를 받아 feature(image)와 mask를 output으로 내보내는 연산이다.

식으로 살펴보자.
$x'$를 구하는 식이 Output feature ($X'$)의 요소를 구하는 식이고, $m'$를 구하는 식이 Output Mask ($M'$)의 요소를 구하는 식이다.

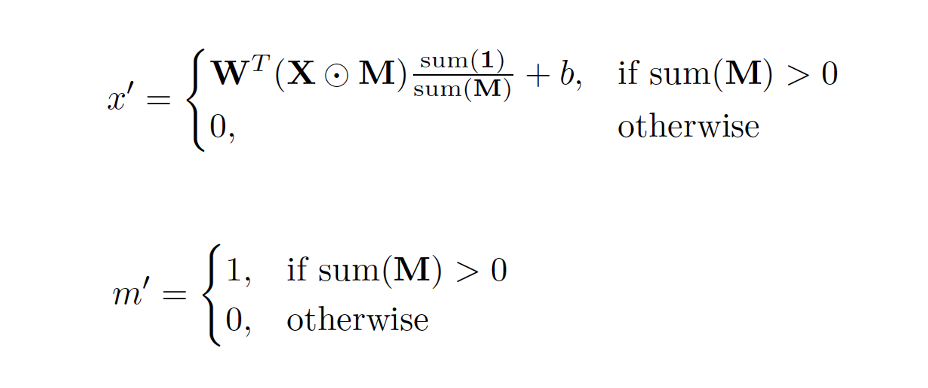
$x'$를 구하는 식을 먼저 살펴보자.

• $W, b$는 Conv filter의 weight와 bias 이다.
• $X$ 는 feature values 이다. (pixel values)
• $M$은 Mask이다. (hole: $0$, non-hole: $1$)
• $\odot$은 element wise multiplication 연산이다.

식을 살펴보면 $x'$는 Mask에서 non-hole인 부분이 한 군데라도 존재한다면 위에 있는 식을 연산한 결과값이고, non-hole인 부분이 한 군데라도 존재하지 않는다면 0의 값을 갖는다. 직관적으로 생각해본다면 Mask에서 non-hole인 부분들만 이용해서 Conv 연산을 통해 hole인 부분을 채워보겠다는 뜻으로 해석할 수 있다.

$m'$는 non-hole인 부분이 한 군데라도 있다면 $1$이고, 모두 hole이라면 $0$이다. $x'$를 구하는 식에서 설명한 것처럼 Mask에서 non-hole인 부분들을 이용해 Conv 연산으로 hole인 부분을 채웠으므로 그 hole인 부분을 메워주겠다는 의미로 해석하면 된다.

즉, Partial Conv 연산을 반복적으로 진행한다면 아래와 같이 Mask의 hole 부분이 점점 채워지는 것을 볼 수 있다.
그림 출처: https://github.com/MathiasGruber/PConv-Keras

2-2. Model architecture

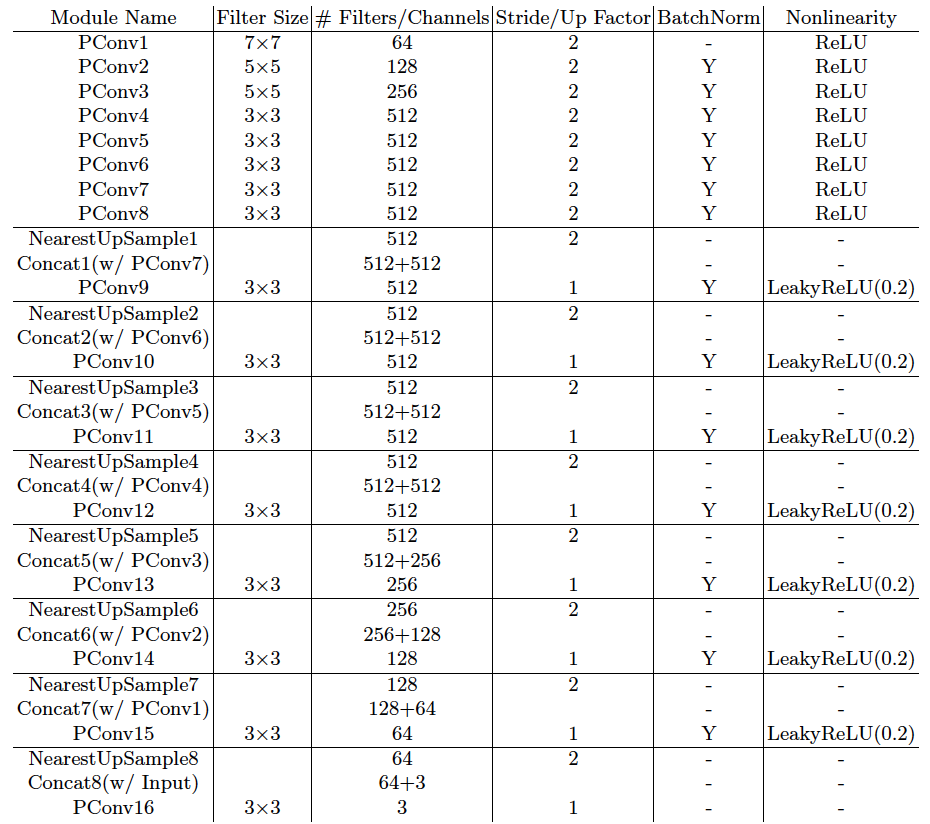모델 구조는 위와 같다.(Table 2)
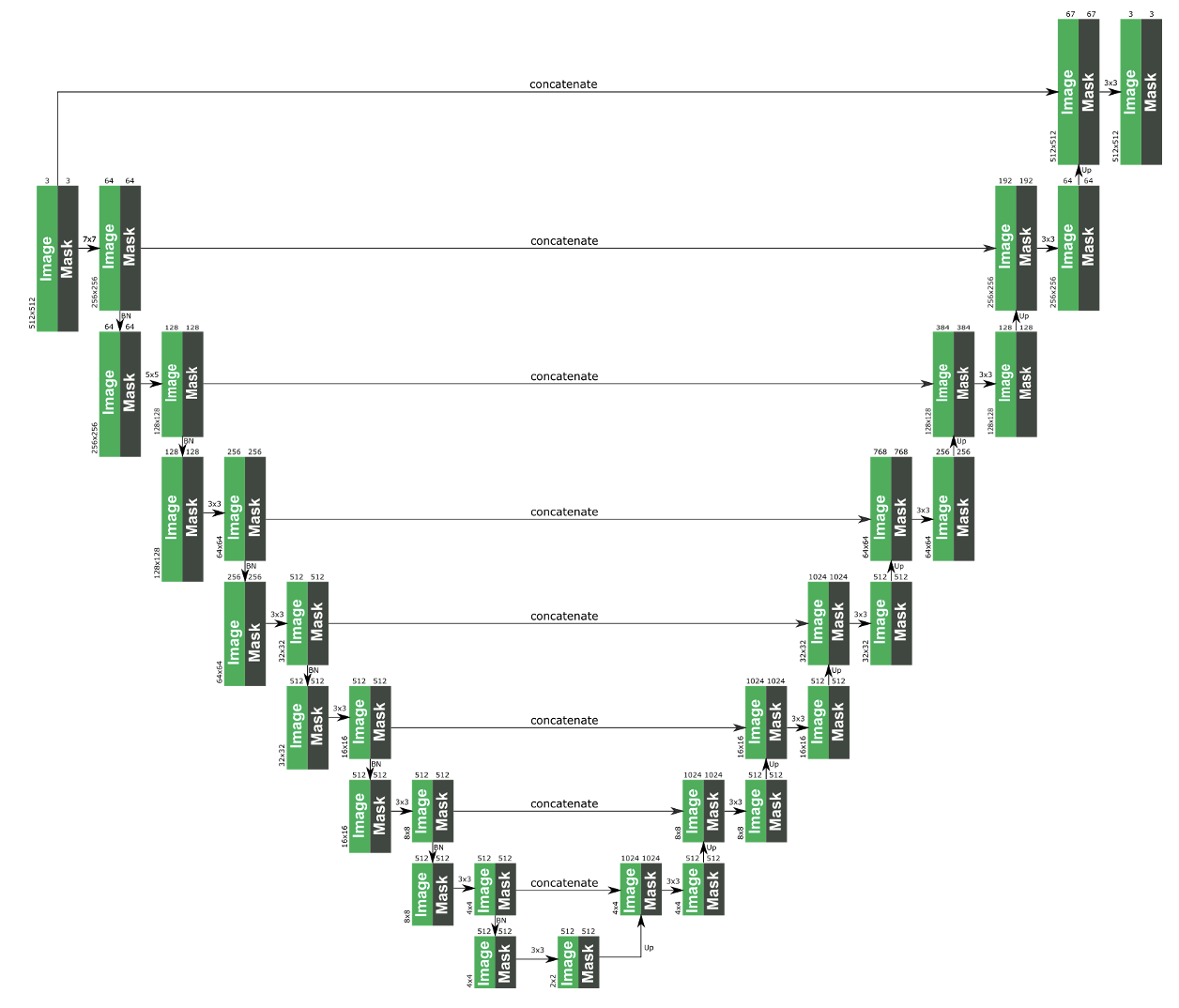그림 출처: https://github.com/MathiasGruber/PConv-Keras

그림으로 나타낸 모델구조이다. 일반 Conv layer 대신 PConv layer로 구성된 U-Net 구조의 모델인 것을 확인할 수 있다.

2-3. Loss function

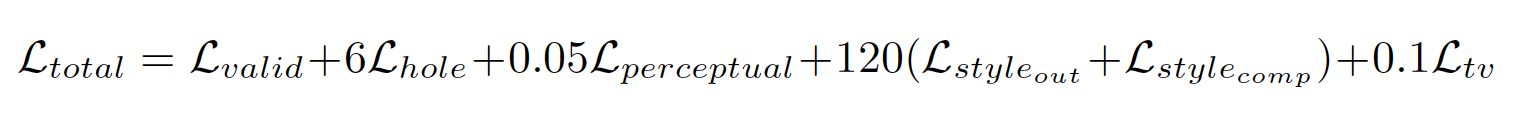Loss function은 위와 같다. 하나씩 살펴보자.

첫 번째로 $L_{valid}$와 $L_{hole}$를 살펴보자.

$L_{valid}=\frac{1}{N_{I_{gt}}} \|M\odot (I_{out}-I_{gt})\|_1$

$L_{hole} = \frac{1}{N_{I_{gt}}} \|(1-M)\odot (I_{out}-I_{gt})\|_1$

• M은 binary mask이다. (hole = $0$, non-hole = $1$)

• $I_{out}$은 모델이 예측한 이미지이고, $I_{gt}$은 ground truth 이미지이다.

• $N_{I_{gt}}$는 $I_{gt}$의 원소의 개수이다. ($= C \times H \times W$)

식을 살펴보면 $L_{valid}$는 non-hole인 부분의 $L_1$ loss인 것을 알 수 있고,
$L_{hole}$은 hole인 부분의 $L_1$ loss인 것을 알 수 있다.

두 번째로 $L_{perceptual}$를 살펴보자.

$\displaystyle L_{perceptual} = \sum_{p=0}^{P-1}\frac{\| \psi_{p}^{I_{out}}-\psi_{p}^{I_{gt}} \|_1}{N_{\psi_p^{I_{gt}}}}+\sum_{p=0}^{P-1}\frac{\| \psi_{p}^{I_{comp}}-\psi_{p}^{I_{gt}} \|_1}{N_{\psi_p^{I_{gt}}}}$

• $I_{comp}$는 $I_{out}$에서 non-hole인 부분을 $I_{gt}$의 픽셀로 치환한 이미지이다.

• $\psi_p$는 p 번째 selected layer의 activation map이다.

  • ImageNet-pretrained VGG16을 이용했다.
  • 이 loss를 구할 때는 pool1, pool2, pool3 layer만 이용했다.

• $N_{\psi_p^{I_{gt}}}$는 $\psi_{p}^{I_{gt}}$의 원소의 개수이다.

첫 번재 항은 $I_{out}$과 $I_{gt}$을 ImageNet-pretrained VGG16를 통과시켜 selected layer로 부터 얻은 각각의 activation map에 대한 $L_1$ loss들의 합이다. (두 번째 항도 $I_{out}$대신 $I_{comp}$가 되었다는 것만 빼면 동일한 연산이다.) 이 두 항을 합한 것이 $L_{perceptual}$인데 연산을 보면 hole인 부분의 $L_1$ loss를 non-hole인 부분보다 2 배 더 중요하게 본다는 것을 알 수 있다. ($I_{comp}$는 $I_{gt}$와 non-hole인 부분은 같다.)

세 번째로 $L_{style_{out}}$와 $L_{style_{comp}}$을 살펴보자.

먼저 gram matrix에 대해 알아야 한다. $\rightarrow$ Gram matrix 설명링크

Style loss에서 style은 feature의 gram matrix로 구할 수 있다. (autocorrelation)
이 논문에서 Style loss는 모델의 output feature의 gram matrix와 ground truth의 gram matrix 간의 $L_1$ loss 이다.

한 번 식과 함게 살펴보자.

$\displaystyle L_{style_{out}}=\sum_{p=0}^{P-1}\frac{1}{C_p C_p} \|K_p((\psi_p^{I_{out}})^T(\psi_{p}^{I_{out}}) - (\psi_p^{I_{gt}})^T(\psi_{p}^{I_{gt}})) \|_1$

$\displaystyle L_{style_{comp}}=\sum_{p=0}^{P-1}\frac{1}{C_p C_p} \|K_p((\psi_p^{I_{comp}})^T(\psi_{p}^{I_{comp}}) - (\psi_p^{I_{gt}})^T(\psi_{p}^{I_{gt}})) \|_1$

• $C_p$는 $\psi_p$의 채널수이다.

• $K_p$는 $\frac{1}{C_p H_p W_p}$로 normalization factor 이다.

$L_{style_{out}}$ 식에서 $(\psi_p^{I_{out}})^T(\psi_p^{I_{out}})$가 $\psi_p^{I_{out}}$ 의 gram matrix이다.

마찬가지로 $(\psi_p^{I_{gt}})^T(\psi_p^{I_{gt}})$는 $\psi_p^{I_{gt}}$의 gram matrix 이다.

이 두 gram matrix의 $L_1$ loss를 구할 수 있고, 이후 정규화를 해준다.

이 연산을 각 selected layer 마다 해서 더하면 $L_{style_{out}}$를 구할 수 있다.

($L_{style_{comp}}$연산은 $L_{style_{out}}$ 식에서 $I_{out}$대신 $I_{comp}$를 사용한다는 것 말고 차이점이 없으므로 생략하겠다.)

정리하자면 $L_{style}$은 $I_{out}$($I_{comp}$)와 $I_{gt}$를 ImageNet-pretrained VGG16에 통과시켜 selected layer마다 나온 각각의 feature들($\psi_p^{I_{out}}, \psi_p^{I_{gt}}$)로 부터 얻은 각각의 gram matrix를 통해 구한 $L_1$ loss의 합과 같다.

직관적으로 이해하자면 feature map의 채널 간 내적 값 (상관관계) 정보가 담긴 각각의 Gram matrix로 loss를 구한다는 것은 두 feature map ($\psi_p^{I_{out}}, \psi_p^{I_{gt}}$)의 채널 간 상관관계를 높이는 방향으로 학습을 하도록 의도한 것으로 해석할 수 있다.

마지막으로 $L_{tv}$를 살펴보자.

$L_{tv} =\sum_{(i, j) \in R, (i, j+1) \in R} \frac{\| I_{comp}^{i, j+1} - I_{comp}^{i, j}\|_1}{N_{I_{comp}}} + \sum_{(i, j) \in R, (i+1, j) \in R} \frac{\| I_{comp}^{i+1, j} - I_{comp}^{i, j}\|_1}{N_{I_{comp}}}$

• $L_{tv}$ (TV loss)에서 $_{tv}$는 total variation의 약자이다.
• Smoothing penalty on $R$, $\rightarrow$ $R$은 hole과 non-hole의 경계의 집합.

식을 살펴보면 $I_{comp}$ 에서 hole과 non-hole의 경계를 기준으로 1 픽셀의 차이를 둔 non-hole인 부분($I_{comp}^{i+1, j}$ or $I_{comp}^{i, j+1}$)과 hole 인 부분($I_{comp}^{i, j}$)의 $L_1$ loss 들의 합이다.

TV loss는 spatial smoothness를 위해 만들어졌다고 한다.
직관적으로 이해하자면 hole인 부분에 이미지를 채워넣을 때 hole인 부분과 non-hole인 부분의 경계가 부자연스러울 수도 있으니 이 점을 보완하기 위한 loss라고 해석할 수 있다.

결국, $L_{total}$ 은

위에서 구한 $L_{valid}, L_{hole}, L_{perceptual}, L_{style_{out}}, L_{style_{comp}}, L_{tv}$의 조합으로 만들어졌다.

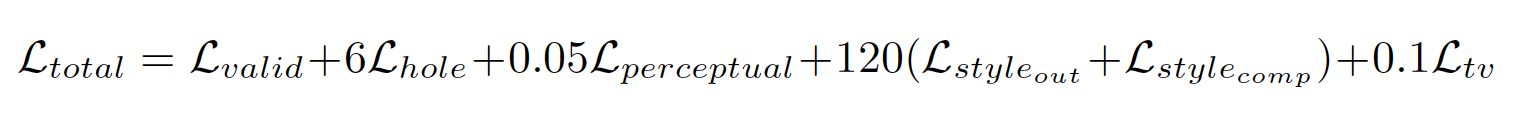
(각 loss에 대한 가중치(계수)는 100 장의 valdiation image로 hyper parameters 조합을 통해 발견했다.)

Figure 3는 Loss별 가중치를 조정해 실험한 결과이다.
(b)와 (f)는 $L_{style}$이 없을 때나 작을 때 어떤 결과를 나타내는지 보여준다. 흐릿해지거나(b), fish scale (f)이 나타났다. (j)는 $L_{perceptual}$을 제거했을 때의 결과이다. grid-shaped artifact가 나타난 것을 볼 수 있다.

3. Experiments

3-1. Irregular Mask Dataset

• 학습을 위해 55,116 개의 mask를 테스트를 위해 24,866 개의 mask를 생성하였음. (mask size는 512 x 512로 고정)

• 여러 기법 (random dilation, rotation, cropping)으로 마스크를 증강.

• Test set으로 사용될 Mask dataset을 border에 hole의 유무로 세분화하였음.
  (외곽 쪽에 hole이 있는 경우, hole을 점점 채워나가는 방식의 Partial Conv의 경우 잘 동작하지 않을 수도 있어 결과를 보고자 이렇게 나눈 것 같음.)
  위 그림에서 1, 3, 5 번 mask는 border가 non-hole인 mask
  2, 4, 6 번 mask는 border에 hole이 포함된 mask

• Image에서 hole이 차지하는 비율로도 카테고리화 하였음. (6 가지)
  (0.01, 0.1], (0.1, 0.2], (0.2, 0.3], (0.3, 0.4], (0.4, 0.5, (0.5, 0.6]
  각 카테고리당 1000 개의 mask를 포함했으며, border 부분에 hole 유무까지 세부 카테고리화 하였음. $\rightarrow 6 \times 2 \times 1000 = 12,000$ 장

3-2. Training Process

• Training Data
  ImageNet, Place2, CelebA-HQ 데이터 셋을 사용
  ImageNet, Place2 데이터 셋으로는 train, val, test 셋으로 나누어 사용하였고, CelebA-HQ 데이터는 27K를 training에, 3K를 test 할 때 사용하였음.

• Training Procedure

  • Weight initialization: He initialization
  • Optimizer: Adam
  • GPU: single NVIDIA V100 GPU (16 GB)
  • Batch size: 6

• Initial Training and Fine-Tuning
  초기 학습에서 hole의 존재가 Encoder 부분에서 BatchNorm이 문제가 되었음. $\rightarrow$ Hole pixel value ($=0$)를 포함해서 mean과 variance를 계산하는 것은 뭔가 이상함. $\rightarrow$ hole의 크기에 따라서 BatchNorm에 영향을 줌.

  이 문제는 Encoder 부분에서 문제가 되지. Decoder 부분에서는 이미 hole이 거의 다 메워져 있기 때문에 문제가 되지 않음.

  이러한 문제를 해결하기 위해 논문에서는 learning rate 0.0002 로 먼저 학습하고 (initial training), 이후 fine-tuning 할 때는 encoder 파트의 BatchNorm layer를 freeze 해놓은 상태에서 learning rate 0.00005로 학습하였음. (fine-tuning)

3-3. Comparisons

Figure 5를 보면 다른 여러 기법들 보다 Pconv를 이용한 Unet의 결과가 더 좋은 것을 볼 수 있다. (Place2 결과 (Fig 6), CelebA-HQ 결과 (Fig 8)도 마찬가지이다. 그림 생략)

정량적인 평가

먼저 사용된 평가지표들에 대해 살펴보자.

• $l_1$: $L_1$ loss (MAE)
• PSNR (Peak Signal to Noise Ratio)
  $\rightarrow$ 화질 손실량을 계산하기 위해 사용 (두 이미지의 픽셀값이 비슷한 지)
  $\\$
  PSNR = $\displaystyle10\log_{10}(\frac{R^2}{MSE})$
  $\\$
  $\\$
  R은 픽셀의 최대값을 의미한다. MSE 식은 아래와 같다.
  $\\$
  MSE = $\displaystyle\frac{\displaystyle\sum_{M, N}[I_1(m, n)-I_2(m, n)]^2}{M*N}$
  $\\$
  우리는 $I_1$과 $I_2$에 각각 모델이 예측한 이미지, Ground truth를 대입할 것이기 때문에 예측한 이미지가 ground truth와 픽셀값이 비슷할 수록 MSE 값이 낮게 나올 것이기 때문에 PSNR 값은 커진다.
  $\\$
  한 마디로 PSNR가 높을수록 모델이 예측한 이미지와 Ground truth 이미지가 비슷한 픽셀값을 가진다는 것을 의미한다.

• SSIM (Structural Similarity Index Measure)
  PSNR과 비슷한 평가지표이지만, 직접적으로 두 이미지 간의 픽셀값을 비교한다기 보다는 휘도(Luminance), 대비(Constrast), 구조(Structure) 이렇게 총 3 가지 측면에서 평가함. PSNR과 마찬가지로 값이 높을수록 좋은 성능이다.
  식은 아래와 같다.
  
  $\\$
  $\\$

각 method별 정량 평가표는 아래와 같다. 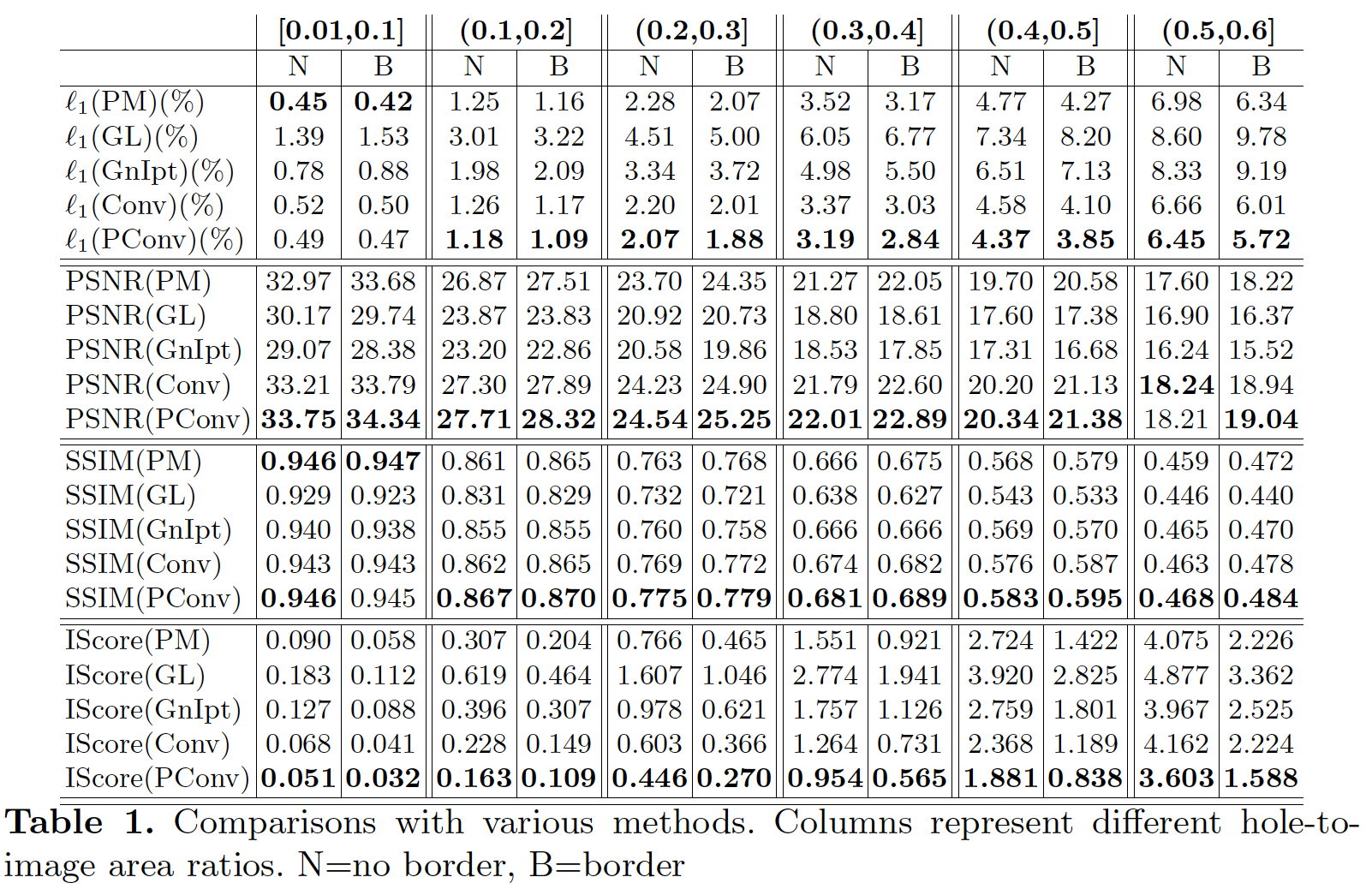다른 여러 기법들 보다 PConv based UNet 모델의 결과가 더 좋은 것을 볼 수 있다.

Discussion

• Hole이 크면 구조물에 대해 잘 복원하지 못한다. (Fig 10)
• 철근이나 문 같은 세부적인 물체들에 대해서는 잘 표현하지 못 한다. (Fig 11)

Extension to Image Super Resolution

• 해상도가 낮은 이미지를 높이는 분야인 super resolution task에서 PConv based-UNet 모델을 사용한 결과 예시이다.

  • (a): 해상도가 낮은 이미지
  • (b): 해상도가 낮은 이미지를 늘린 이미지이다. 늘리면서 hole이 일정한 격자 간격으로 생긴 것을 볼 수 있다.
  • (c): 이미지 (b)의 mask이다.
  • (d): 모델이 예측한 이미지
  • (e): Ground Truth

• 다른 여러 Super resolution 관련 method와 비교해본 결과이다.

Reference

Paper
https://arxiv.org/abs/1804.07723

PSNR
https://m.blog.naver.com/mincheol9166/221771426327

SSIM
https://xoft.tistory.com/3