📗 빅데이터를 통찰하는 힘 : 실무활용 편
- 2장 통계학이 '최강인 또 하나의 이유 (2)
가설 검정
-
귀무가설 : 우선적으로 생각한, 자신의 주장을 완전히 뒤짚어 엎는 가설
-
p-value : 귀무가설이 성립한다는 가정 아래 실제 데이터 또는 그 이상으로 귀무가설에 반하는 데이터가 얻어지는 확률 (5% 미만)
-
신뢰구간 : 존재할 수 없는 귀무가설과 부정할 수 없는 귀무가설의 경계선이 어디부터 어디까지라는 범위를 나타내는 것 109쪽
Z 검정
: 귀무가설 하에서 검정 통계량의 분포를 정규분포로 근사할 수 있는 기초적인 추론통계검정
: 두 그룹의 비율/평균 차이가 우연한 데이터의 불규칙성에 의해 생겨난 것인지 아닌지 생각하기 위한 방법 (우연한 차이인지, 의미있는 차이인지) 121쪽
-
z변환 : 본래부터 어떤 값이든 평균값에서 표준오차가 얼마나 벗어나 있는가라는 값으로 변환하는 것
-
가정 : 표본 크기가 30보다 크다(이하라면 t-test), 모집단에서 동일한 확률로 선택되어야 함.
-
조건 : 독립변수의 독립성, 정규성, 등분산성
- 어떤 불규칙성을 지닌 데이터에서 뭔가의 값을 산출하는 한 거기에는 반드시 표준오차가 존재한다. ... 평균값/비율의 차이도 다수의 데이터만 있으면 정규분포에 수렴한다. 따라서 평균과 비율의 차이를 가설검정할 수도 있으며 표준오차로 신뢰구간을 구할 수도 있다. 118쪽
'비율'과 '평균' 차이의 의미를 판단하는 z검정
119쪽
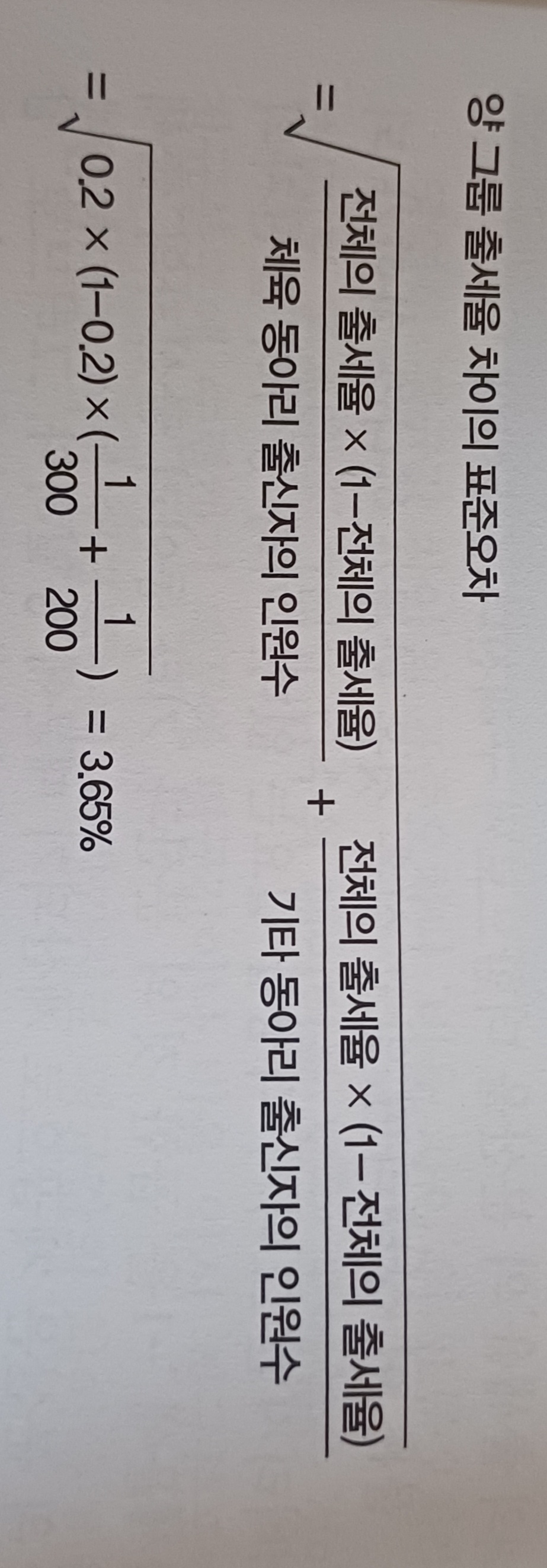
비율 차이의 표준오차를 구하는 방법은
- 비율이란 어떤 상태를 취하는가 (1) 취하지 않는가(0) 하는 이항변수의 평균이라는 생각에 근거하면 이항변수의 분산은 비율 x (1-비율)로 구해진다.
- '분산의 가법성'이라는 성질만 알면 이 표준오차의 계산 방법을 이해할 수 있다. 분산의 가법성은 두 확률 변수가 독립적일 때, 그 합의 분산이 각 확률 변수의 분산의 합과 같다는 성질을 말한다. 이를 활용한다.
예를 들어
체육 동아리 출신자의 출세율과 기타 동아리 출신자의 출세율을 더한 것의 분산은 체육 동아리 출신자의 출세율의 분산과 기타 동아리 출신자의 출세율의 분산을 더함으로써 구해진다.
차이를 알고 싶다고 해도 -1을 곱한 값과 원 값의 분산은 제곱으로 계산하기에 동일하다. 그러므로 양쪽 값을 더하는 것의 분산을 구하는 것처럼 양쪽 값의 차이 역시 분산 가법성에 의해 구해진다.
정리하자면
- 양 그룹에 정혀가 차이가 없을 경우 양 그룹 공통의 출세율을 구한다.
- 양 그룹 공통의 원시 데이터의 분산은 앞에서 언급했듯이
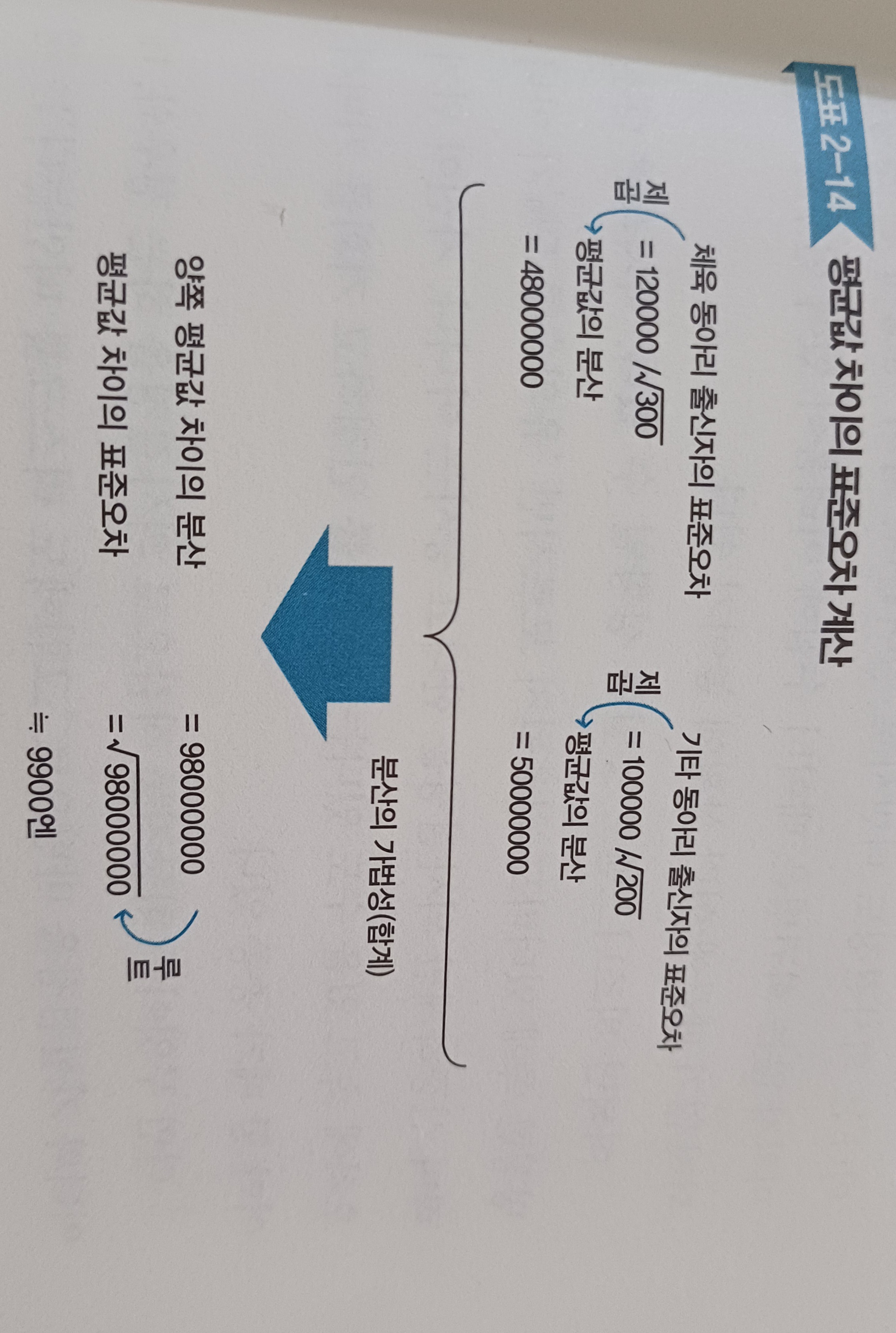
출세율x (1-출세율)의 계산으로 구한다. - 여기서 분산 가법성을 사용해 모두 더하고자 하는 것은 원시 데이터의 분산이 아닌
그룹별 출세율의 분산이다. 그룹별 출세율의 분산은 이를테면각 그룹 출세율의 표준오차의 제곱이다.- 그러므로 원시 데이터 분산을 데이터 수의 루트로 나눈 것을 제곱하고, 분산 가법성에 근거하여 모두 더하면
양 그룹의 출세율의 차이의 분산이 구해진다. 마지막으로 이 분산의 루트를 생각하면 그것이양 그룹 출세율 차이의 표준오차가 되는 것이다.
t 검정
: 모집단의 분산이나 표준편차를 알지 못할 때, 표본으로부터 추정된 분산이나 표준편차를 이용하여 두 모집단의 평균의 차이를 알아보는 검정방법
- 목적 : 두 개의 집단의 차이 유무를 확인하기 위해
- 가정 : 종속변수가 양적 변수일 때, 모집단의 분산이나 표준편차를 알지 못할 때, 모집단의 분포가 정규분포일 때
- 조건 : 독립변수의 독립성, 정규성, 등분산성
출처
z검정 보다 t검정을 우선 선택하는 것이 기본인 이유 130쪽
현재 평균값 차이가 의미 있는지 아닌지 생각하는 경우 일반적으로 t검정을 사용한다. 통계학은 소(를 위한 분석 방법)는 대(를 위한 분석 방법)을 포용한다는 말이 성립한다. 즉 수 천건 데이터로 t 검정을 하는 것은 문제가 없다.
카이제곱 검정
- 카이제곱분포는 평균값이 0, 분산이 1의 정규분포를 따르는 x 변수를 생각했을 때 이 변수의 제곱을 전부 더한 것의 분포이다.
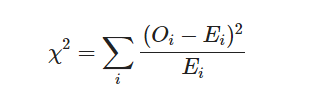피어슨 카이제곱 검정
O는 관찰값, E는 기댓값이다. 적합도 검정(독립변수1인 기대되는 빈도의 분포 비교)과 교차분석을 이용해 카이제곱 분포를 이용하는 경우가 많다.
-
카이제곱분포의 성질에 근거하여 데이터 수에 의해 혹은 카이제곱분포의 자유도별로 '평균값 차이'가 '평균값 차이의 표준오차'의 몇 배 이내로 수용될 확률이 몇 %인지를 계산하기 위한 분포 = t 분포 133쪽
-
중심극한정리에 따르면 샘플이 무수히 많고 합을 이용해 오차를 정의하면 그 오차는 정규분포이다. 따라서 ✨카이제곱분포를 이용해 오차를 검증하면 오차의 유의차를 판별 할 수 있다.✨
데이터 수가 한정된 경우 쓰이는 '피셔의 정확검정'
교차표 어떤 칸에도 가급적 10, 최저 5 이상의 숫자가 들어가는 경우 z검정을 해도 문제없다는 것이 관례적으로 허용되는 기준이다.
z검정을 사용하기 어려운 상황이라면 피셔의 정확검정 혹은 피셔의 직접확률검정을 사용하는 방법이 있다. 정확한 확률 계산으로 p값을 산출한다.
분산분석
: N개의 집단을 비교하는 통계적 분석, t검정과 비슷하나 변수의 수가 다르다.
: 분산 개념을 이용해 수준 평균들 간의 차이가 있는지를 파악한다.
: 각 편차의 제곱합을 자유도로 나누어 값을 얻는다.
- 조건 : 정규성, 등분산성, 독립성
- 가정 : 독립변수가 이산형/범주형 자료 & 종속변수가 연속형 자료 & 3개 이상의 집단 간 평균 비교분석
위 3 검정 비교
✨ z검정, t검정, 분산분석 모두 그룹 간 평균값 차이가 어느 정도인지 p-값을 산출할 수 있다.
✨ 실제 비즈니스에서 분산분석과 카이제곱 검정은 별로 사용되지 않는다.
분산분석 귀무사설이 '모든 그룹 간 평균값 차이가 전혀 없거나' 혹은 '모든 그룹 평균값은 사실상 완전히 동일'한 것이기 때문이다. 구체적으로 어떤 차이가 있는지를 파악하기 어렵다. 145쪽
카이제곱검정이라면 선택항목 간 비교로 '구체적으로 어떤 그룹이 어떻게 다른가'를 대답할 수 있다. 하지만 p값 갯수가 늘어나면 검토해야하는 값이 기하급수적으로 늘어나고 실수를 저지를 확률이 크게 늘어난다(검정의 다중성).
위와 같은 상황을 줄이기 위해 다중비교 분석 방법을 사용한다.
1) 본페로니 방법 사용 : p값별로 유의 여부의 판단기준을 5% 유의수준을 검정한 횟수로 나눈 값을 사용한다.
2) 기준 카테고리를 하나 정한 다음 비교 : 모든 경우의 수를 비교하는 것이 아니라 하나의 기준 카테고리와 나머지 그룹과의 차이를 고려한다,
3) 탐색적 p값과 검정적 p값을 적절히 비교한다.
변수 종류에 따라 어떤 검정을 사용해야할까
- 설명변수, 아웃컴이 모두 질적인 경우 : z검정, 카이제곱검정으로 아웃컴 비율 비교
- 설명변수 질적, 아웃컴 양적인 경우 : z검정, t검정
🔎 책 내용을 잘 정리한 다른 블로그 글
