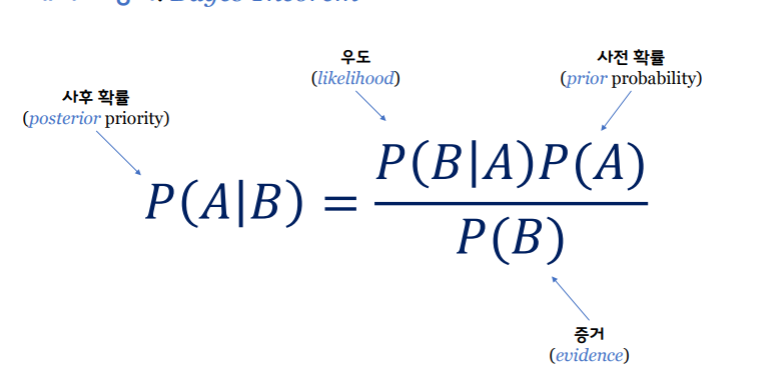통계 | 기초, z분포, 베이즈정의, 포아송분포, t분포 개념모음

정의

• 요소(elements) : 수집되는 대상

• 변수(variable) : 요소의 특성

• 관찰값(observation) : 특정 요소의 수집된 측정치의 집합

• 자료 집합 : 자료값 총수 = 요소의 수 X 변수의 수
  

• 측정 척도 : 명목 / 등간 / 서열 / 비율

• 분류 : 질적 자료(범주형) / 양적 자료(수치형)

-질적자료 : 명목, 서열 척도 중의 하나, 기초나 명칭 등 각 요소의 속성을 분별하는데 사용
-양적자료 : 이산형, 연속형으로 나타내며 일반적인 산술연산이 사용할수 있고 숫자로 항상 표시

• 시간으로 자료 분류
  -횡단면 자료(cross-sectional) : 동일한 시점에 수집된 자료
  -시계열 자료(time series) : 여러 시점에 걸쳐 수집된 자료

이미지 출처

자료표현

• 질적자료 : 도수분포(일반/상대/백분율), 막대그래프, 파이차트
  -도수분포 : 겹치지 않게 나눈 각 계급별 항목의 도수, 개수를 표로 요약하는 것

• 양적자료 : 도수분포(일반/상대/백분율), 히스토그램, dot plot, 누적분포

표준정규 확률분포 (z분포)

: 정규분포를 따르는 확률변수의 평균 0, 표준편차 1일 때
그 확률변수는 표준정규확률분포를 따른다고 한다.

• 표준정규분포로 변환

z = (x - mean) / std

• 표준정규밀도함수
  

베이즈 정리(bayes' Theorem)

: 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리 (사전확률을 갱신하는 방법 제공)

• process : 사전확률 > 새로운 정보 > 베이즈 정리 적용 > 사후확률

• 공식

출처

• 베이즈 정리는 상호 배타적이며, 모든 사건의 합집합이 전체 표본 공간이 되는 사건들의 사후확률을 구할 때 적용

포아송 분포(Poisson distribution)

: 확률론에서 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산 확률 분포.
시간 또는 공간의 일정한 구간에서 발생하는 사건의 횟수를 추정하는데 유용하다.

예) 송판의 14feet 내에 있는 옹이 구멍의 개수, 시간당 요금소에 도착하는 자동차의 대수

• 속성

1. 동일한 길이의 어떤 두 구간에서 사건발생확률은 동일하다.
2. 각각 사건발생은 상호독립적이다.
3. 포아송 분포의 특성: 평균과 분산이 같다

• 공식
  

t분포

: 모집단 표준편차를 알 수 없을 때 표본 평균과 모집단 평균 사이 표준화된 거리를 설명 (모집단이 정규분포라는 것을 가정)

-자유도가 증가할수록 t분포의 변동성이 낮다. 표준정규분포와의 차이가 점점 줄어든다. (자유도 100을 넘으면 z값 사용 가능)