88. Merge Sorted Array
문제
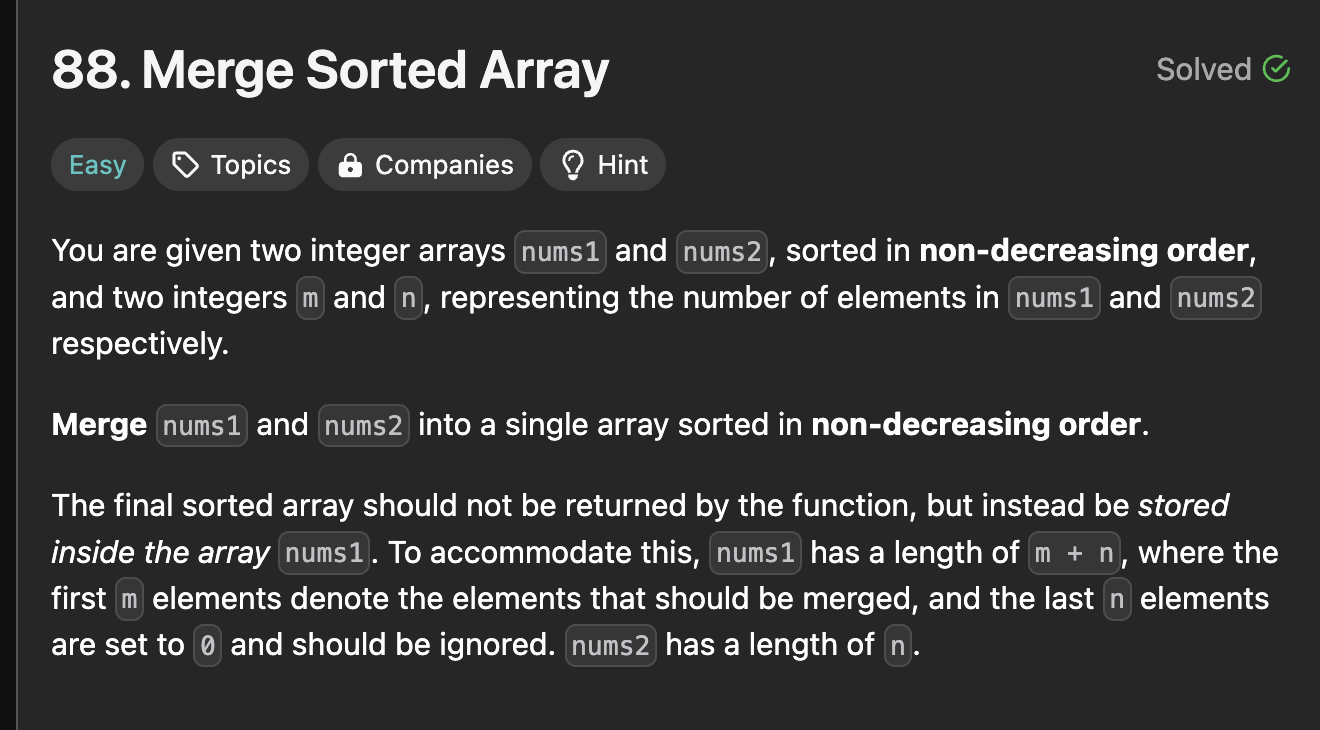
테스트 케이스
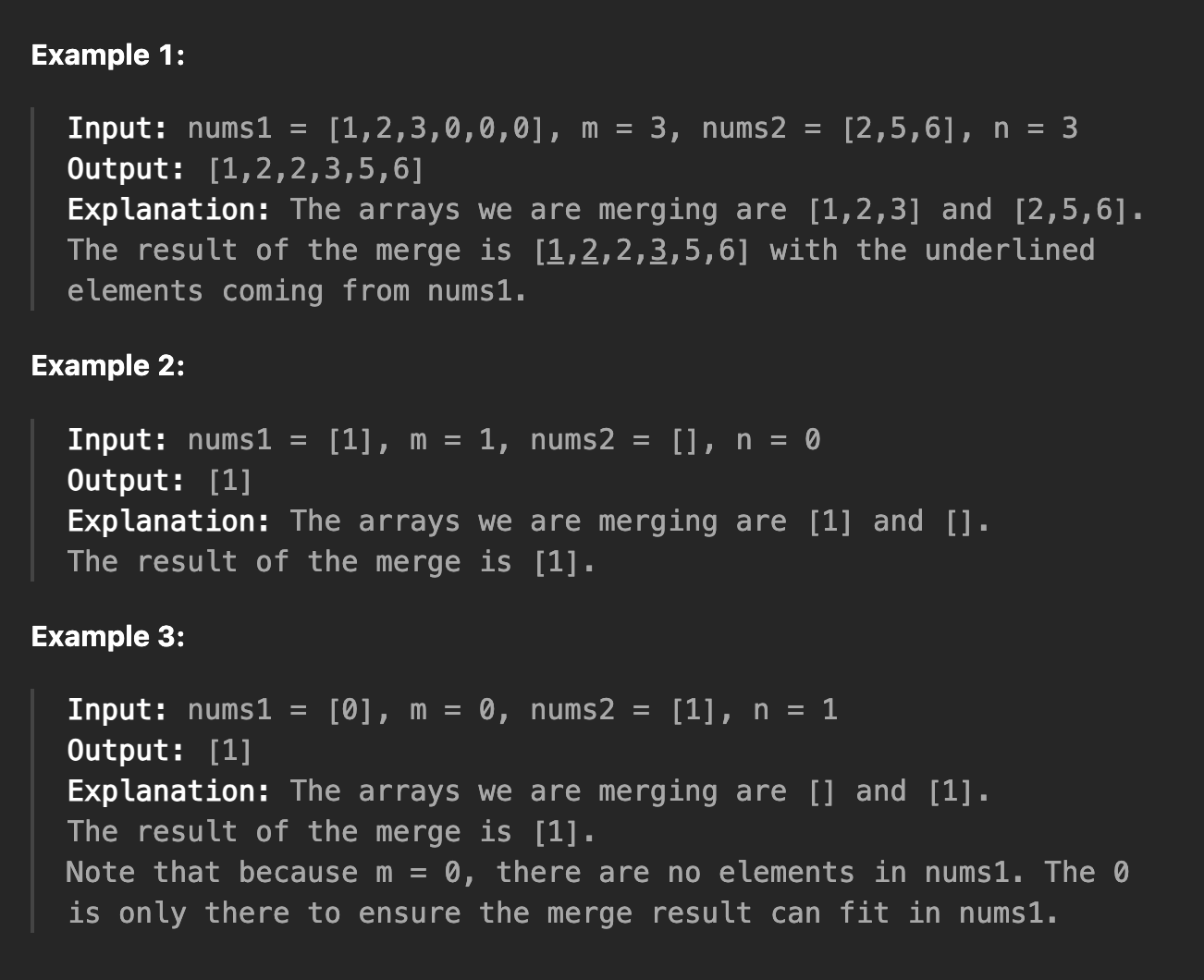
제약 사항
시간 낭비
Merge-Sorted-Array라는 문제 이름을 보자마자 가장 먼저 떠올랐던 키워드는 merge-sort(합병정렬)였다.
최근 분할 정복(divide&conquer)에 대해서 공부했는데, 분할 정복 방법의 대표적인 예시가 합병 정렬(merge-sort)다. 즉, 공부했던 방식으로 접근하면 문제를 비교적 쉽게 풀 수 있겠다는 생각을 했다.
근데 뭔가 이상했다.
공통된 sub-problem이 무엇이며 어떤 것을 재귀함수로 만들어야하지?
머리를 굴려봐도 내가 공부한 합병 정렬(merge-sort) 방법으로는 풀리지 않았다.
곰곰히 생각해보니 내가 하려던 합병 정렬(merge-sort)은 순서가 뒤죽박죽인 하나의 배열을 오름차순 또는 내림차순으로 정렬하는 것이고,
이 문제는 이미 정렬되어 있는 두 개의 배열의 요소를 비교하며 하나의 배열로 합치는 것이다.
merge랑 sort라는 키워드만 보고 합병 정렬(merge-sort)로만 한참 동안이나 생각했다는게..
실전이었으면 이미 광탈이다.
난 다시 문제를 꼼꼼하게 읽으며 분석해보았다. 진작에 그랬으면 좋았을걸.
문제 분석
non-decreasing-order로 정렬될 배열nums1과nums2를 받는다.- 정수
m과n을 받는다. m은 배열nums1의 요소의 수를 나타낸다.n은 배열nums2의 요소의 수를 나타낸다.- 배열
nums1과 배열nums2을 하나로 합쳐라 (non-decreasing-order)
제약 사항
nums1을 새로 만들어서 리턴하지 말고,nums1의 요소를 변경해야 한다.
참고
non-decreasing-order는 현재 요소가 이전 요소보다 "작지 않은 것" => 동일하거나 큰 것increasing-order는 현재 요소가 이전 요소보다 "큰 것"
문제를 분석하며 이해하기 힘들었던 부분
To accommodate this, nums1 has a length of m + n, where the first m elements denote the elements that should be merged, and the last n elements are set to 0 and should be ignored. nums2 has a length of n.
위 말은 정수 n이 nums2의 요소 길이를 나타냄과 동시에 nums1에서 채워지지 않는 부분을 나타낸다는 것을 이해하는데 시간이 꽤 소요되었다.
(문제를 꼼꼼하게 읽으며 분석하는 연습이 필요하다)
첫 번째 접근
이 문제에서 핵심은 nums1의 요소와 nums2의 요소를 비교해가며 처리하는 것이다.
비교를 하며 두 가지 경우가 나온다.
case-1.
nums1의 요소가nums2의 요소보다 작거나 같은 경우
(1)nums1의 현재 요소를 현재 인덱스 위치에 그대로 둔다.
(2)nums1의 다음 요소와nums2의 현재 요소를 비교한다.
case-2.nums1의 요소가nums2의 요소보다 큰 경우
(1)nums1현재 요소의 인덱스 위치에nums2의 현재 요소를 넣는다.
(2)nums1의 현재 요소와nums2의 다음 요소를 비교한다.
반복 루프를 돌며 각 요소들을 비교&처리 해주고, nums2의 요소가 nums1의 '0'부분들을 전부 채워주었을 때 루프를 멈추기로 했다.
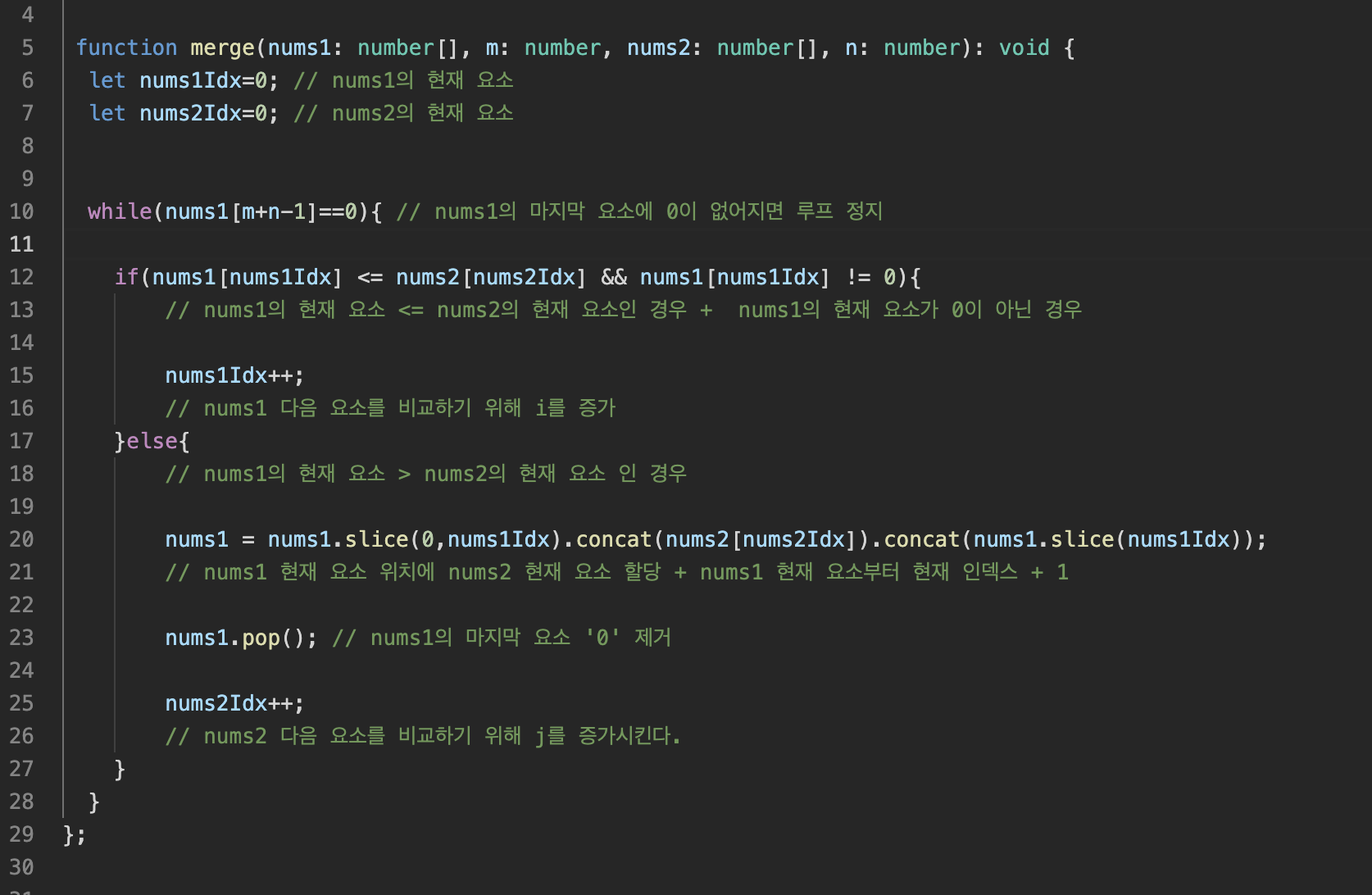
위와 같이 코드를 짜고 테스트코드를 돌려보았다.
🚨 첫 번째 문제 발생
while 반복문이 끝나고 num1을 console을 찍어보면 정답과 일치하지만,
처음 문제에서 주어진 제약 사항을 지키지 않아 테스트를 통과하지 못했다.
제약 사항
nums1을 새로 만들어서 리턴하지 말고,nums1의 요소를 변경해야 한다.
(nums1을 새로 만들지 말고 변경하라 했는데 재할당하고 있네)
두 번째 접근
지금까지의 상황을 정리해보면,
nums1의 현재 요소가nums2의 현재 요소보다 큰 경우 (else 조건)nums1현재 요소의 인덱스 위치에nums2현재 요소를 할당하고,nums1현재 요소를 뒤로 한칸씩 밀어내야한다.
(+)nums1을 새로 만들지 않고, 배열 안 요소들을 변경하여 위 조건을 충족해야한다.
nums1의 요소들 중 뒷 부분에 위치한 0은 없어져야 하는 요소들이니,
else 조건에 반복 루프를 한번 더 돌려서nums1의 요소를 한 칸씩 뒤로 직접 할당하고- 뒷 부분에 위치한
0을 제거하며nums1의 길이를m+n으로 유지
하는 방식으로 접근해보았다 .
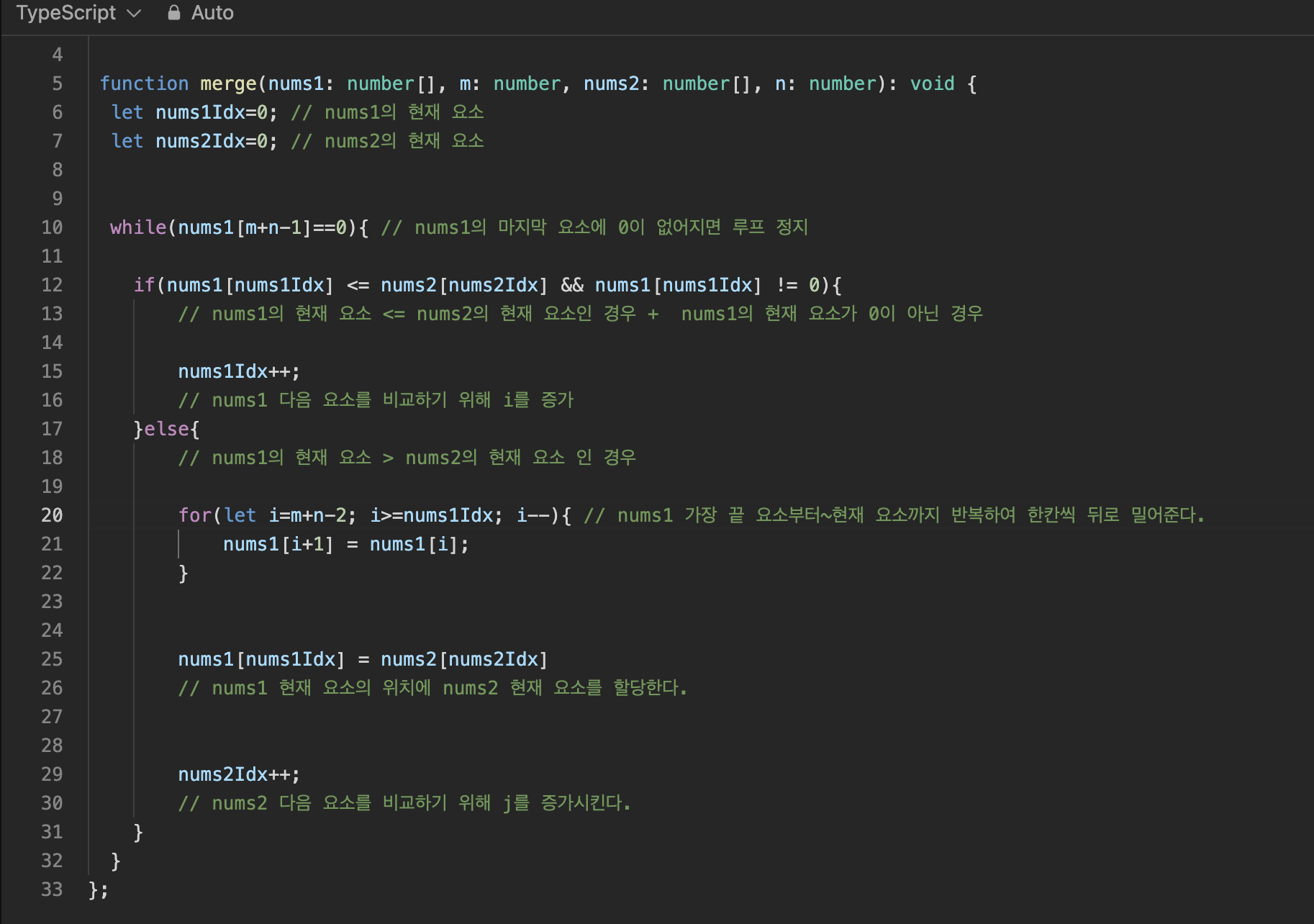
이렇게 하니, example들은 모두 통과했다.
🚨 두 번째 문제 발생
들뜬 마음으로 submit을 했으나 기쁜은 잠시 반도 통과하지 못했다.
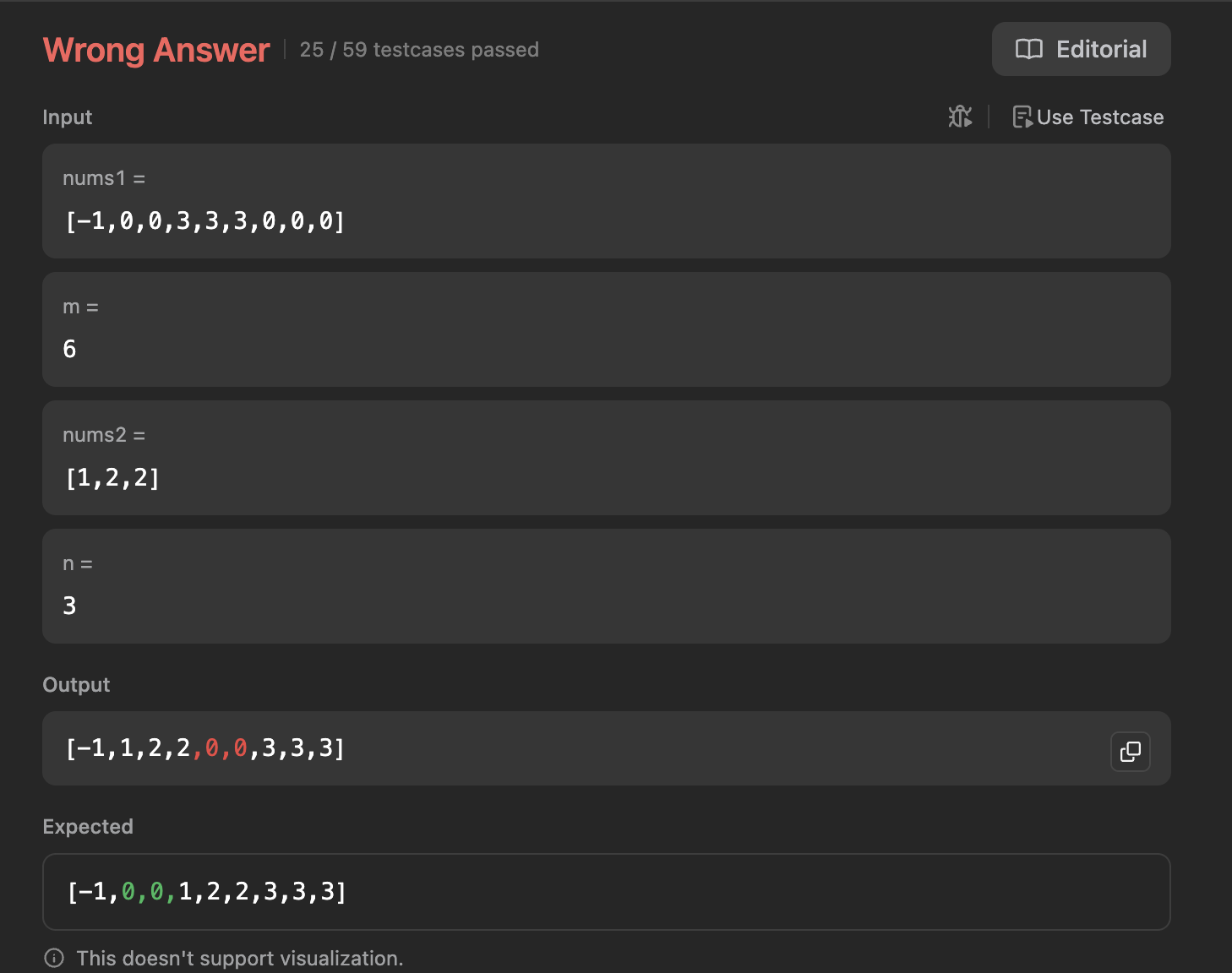
nums1의 유효한 요소들에 정수 0이 포함되는 케이스를 생각하지 못했다.
예를 들어, nums1이 [-1,0,0,3,3,3,0,0,0]이고 nums2가 [1,2,2]라고 가정해보자.
nums1[nums1Idx]값이 유효한 0임에도 else 조건으로 빠지게 된다.
if(nums1[nums1Idx] <= nums2[nums2Idx] && nums1[nums1Idx] != 0)
-1,1,0,0,3,3,3,0,0
-1,1,2,0,0,3,3,3,0
-1,1,2,2,0,0,3,3,3nums2의 요소들 [1,2,2]가 nums1의 유효한 요소 0보다 앞에 오는 문제가 발생해버린다.
if 조건문에 nums[nums1Idex] != 0 을 추가했던 이유는 nums1=[0] 인 경우를 충족시키기 위해서였는데, 꼬여버렸다.
세 번째 접근
정답에 근접한 느낌이 들었다.
코드를 약간만 변경하면 모든 조건을 충족 시킬 수 있을 것 같았다.
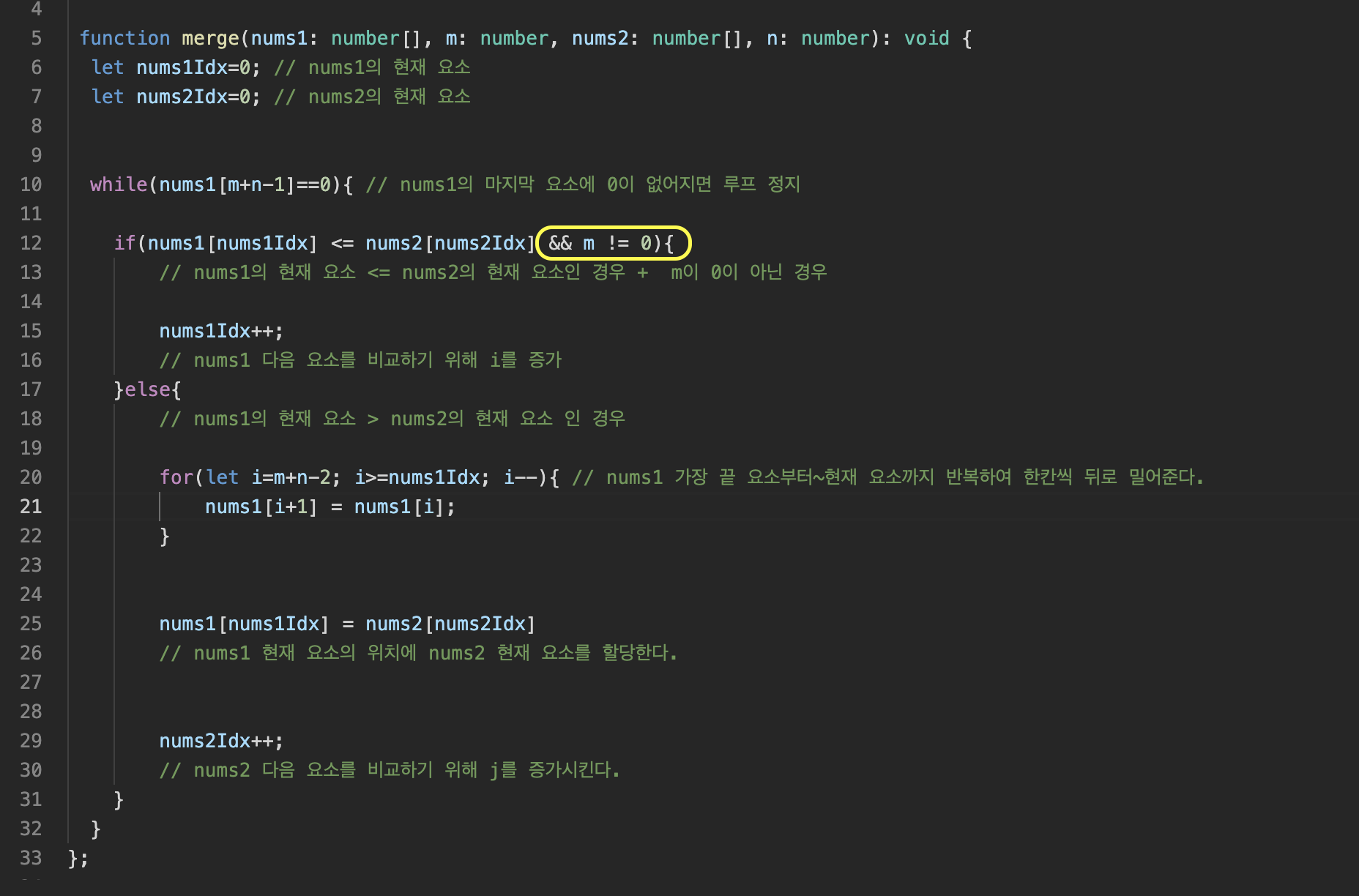
문제가 되었던 if 조건 중 nums1[nums1Idx] != 0을 m != 0 으로 변경해주었다.
nums1=[0] 인 경우를 경우를 충족하면서 동시에 nums1이 [-1,0,0,3,3,3,0,0,0]인 케이스 들도 충족시키기 때문이었다.
🚨 세 번째 문제 발생
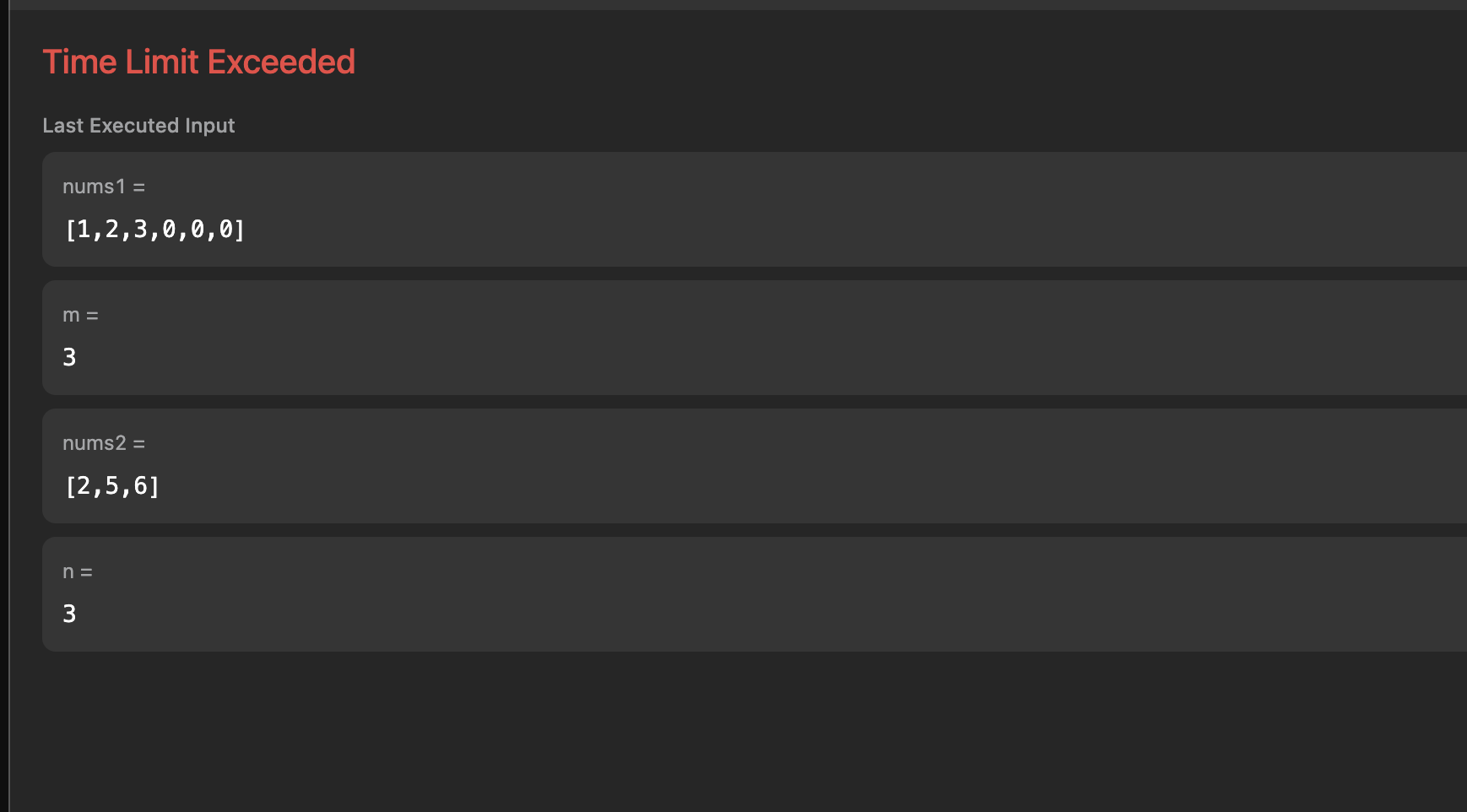
이번에는 첫 번째 테스트 케이스에서 무한루프가 도는 문제가 발생했다.
nums1이 1,2,3,0,0,0 이고 nums2가 [2,5,6]인 경우 루프를 탈출하지 못한다.
하나의 테스트 케이스를 통과하기 위해서 코드를 변경하니 다른 테스트 케이스를 못하는 경우 발생. 짜증이 몰려온다.
네 번째 접근
코드를 완전 잘못 짰다고 생각하고 다시 접근해보았다.
지금까지 코드를 다시 살펴보니 while 반복 루프의 탈출 조건이 잘못되었던 것 같다.
결국 핵심은 nums1의 요소와 nums2의 요소를 비교하는 것인데,
nums1의 뒤에는 없어져도 되는 요소 0 이 있다.
또한 nums1과 nums2는 이미 non-decreasing-order로 정렬되어있다.
위 특징을 잘 조합해보면,
각 배열의 요소들을 앞에서부터 비교하며 채우고 밀어내는 방식이 아니라,
⭐️뒤 요소부터⭐️ 비교해가며 nums1의 없어져도 되는 0의 인덱스 위치에 nums2의 요소를 바로 직접 할당하는 방식이 더 적절해보인다.
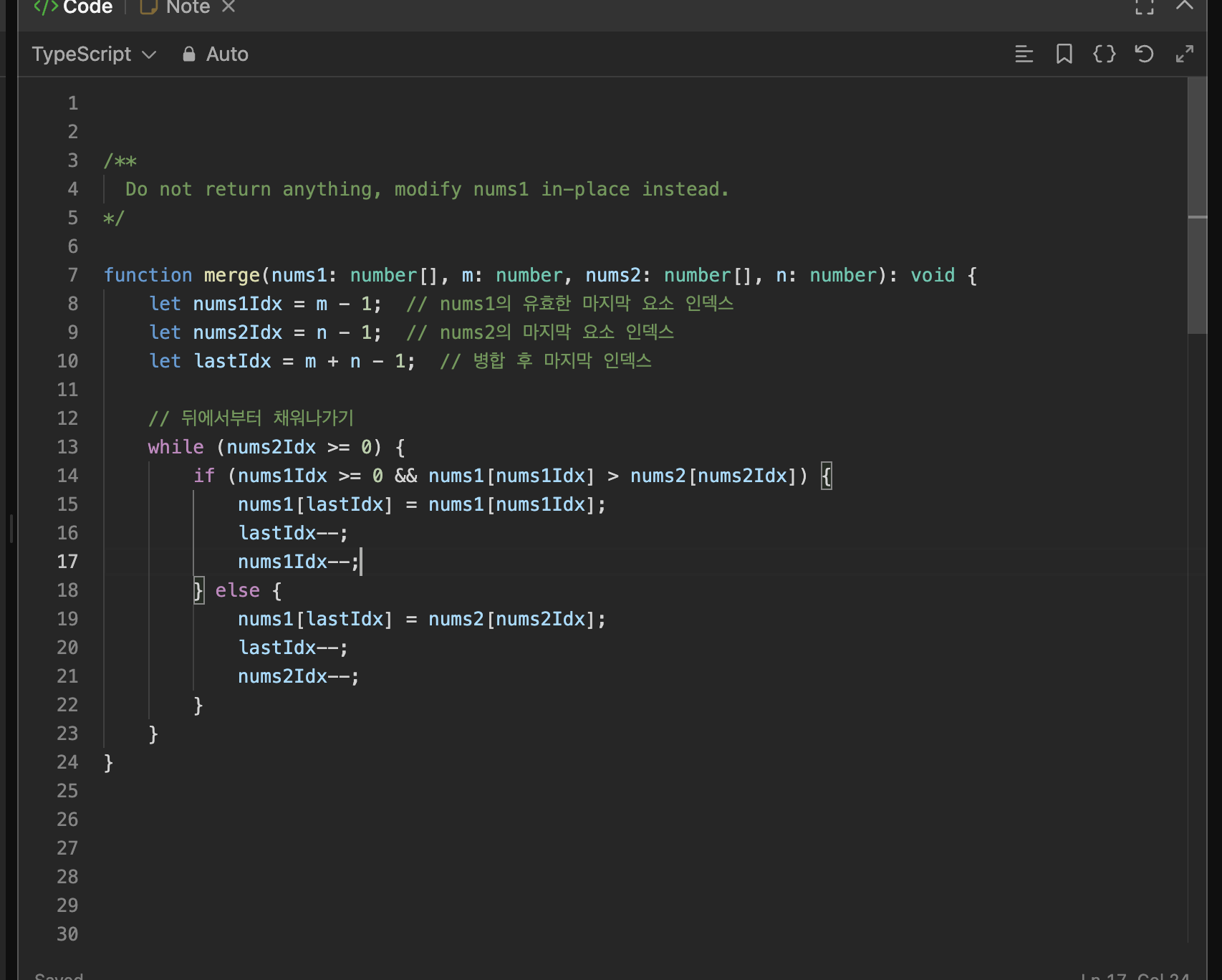
뒤 요소부터 앞 요소로 비교하기 때문에 nums2의 현재 인덱스가 첫 요소의 인덱스인 0보다 작아지는 경우에 반복문이 끝나도록 설정하였다.
'nums1의 유효한 요소들의 인덱스'와 '전체 인덱스'를 구분하여 변수를 설정했다.
nums1의 유효한 마지막 요소와 nums2의 마지막 요소를 비교한다.
case-1.
nums1의 유효한 마지막 요소가 큰 경우
(1)nums1의 유효한 마지막 요소를 nums1의 마지막0부분에 할당해준다.
(2)nums1의 마지막에서 앞 요소와nums2의 마지막 요소를 비교한다.
case-2.nums1의 유효한 마지막 요소가 작거나 같은 경우
(1)nums2마지막 요소를 nums1의 마지막0부분에 할당해준다.
(2)nums1의 마지막 요소와nums2의 마지막에서 앞 요소를 비교한다.
이렇게 되면 인덱스간 충돌이 발생하는 문제를 방지할 수 있다.
또한 m+n의 크기만큼 시간이 걸리기 때문에 시간 복잡도도 O(m+n)으로 꽤 좋은 편이다.
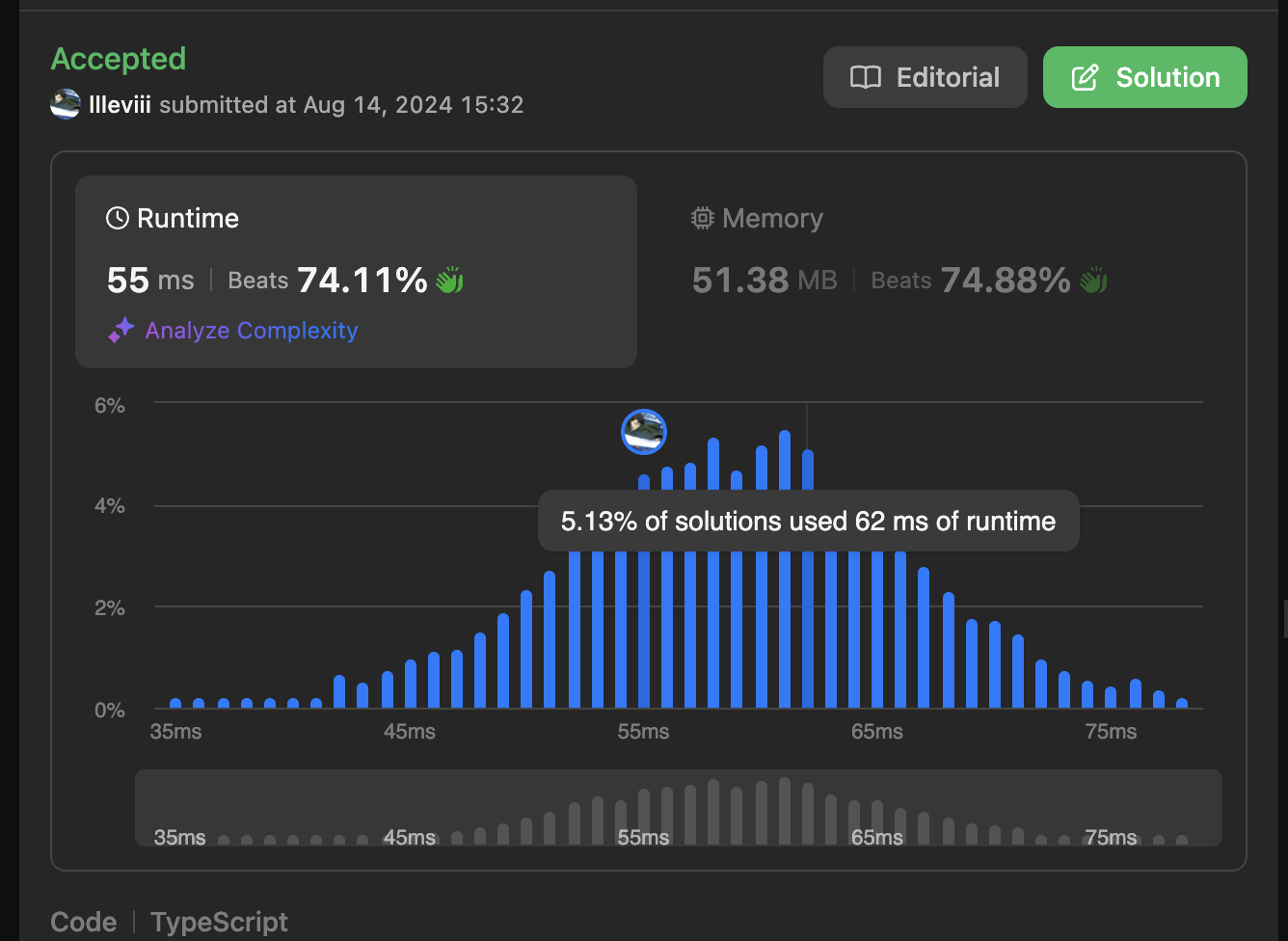
마무리
문제를 무작정 푸는게 아니라, 문제를 깊게 분석하고 발생할 수 있는 엣지 케이스를 최대한 생각해보며 문제에 접근하자. (example 최대한 참조하기)
단순한 코드 변경으로 edge-case를 통과하려는 마음을 버리고,
edge-case들을 충족시키는 전체적인 접근 방식을 고민해보자.
