1-1. Q-learning

An agent can move up, down, right, left. It moves randomly until it reaches the goal. This journey is called 'the episode'. The episode is repeated until the agent finds the shortest path between start and the goal.

In the Q-learning algorithm, we use greedy action. We give scores to the agent for every movement. The greedy action is that the agent moves to the highest scored direction.
At the first episode, the agent has no information of direction score. So it moves randomly. Then, how do we give scores to the agent's movement?

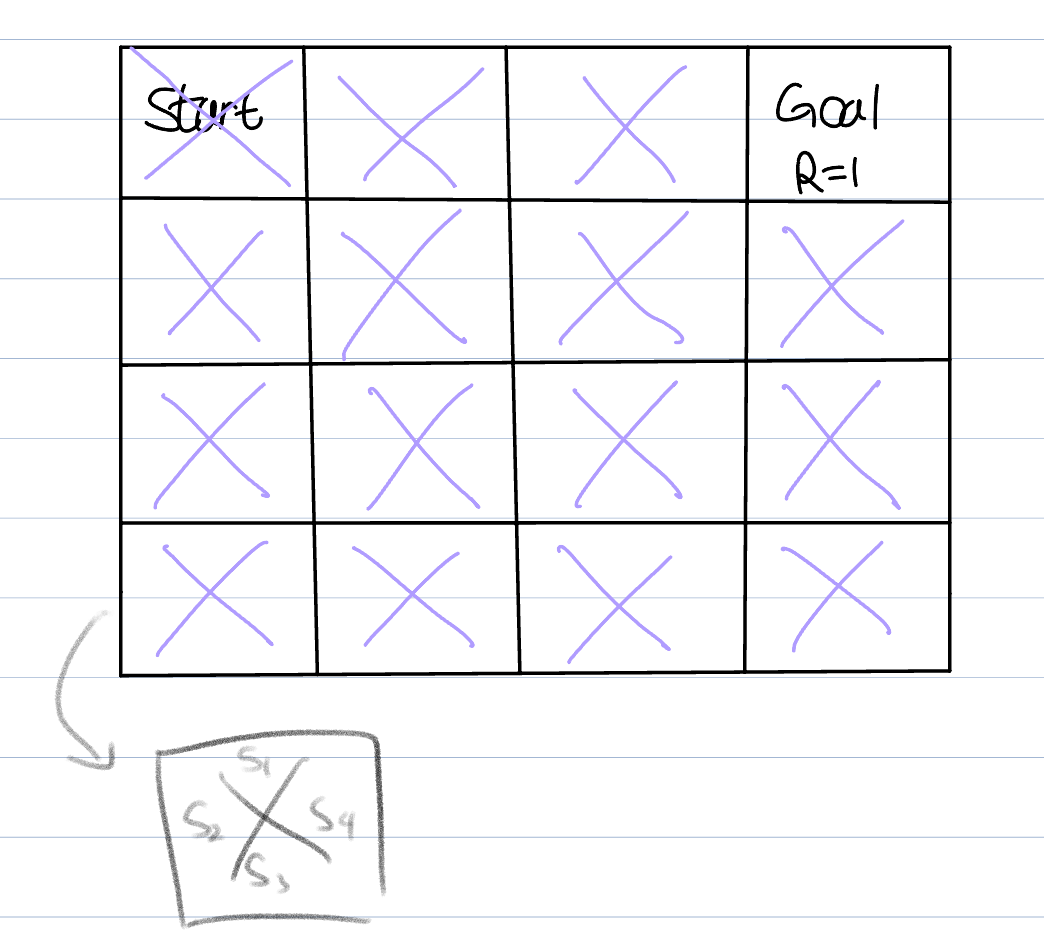
We add 4 states to every box(each state expresses the score in each direction : up -> s1 / down -> s2 / right ->s3 / left ->s4). We initialize every scores to zero. And let's get back to the first episode. let's assume that the agent reaches the goal after visiting the green box(see the figure)

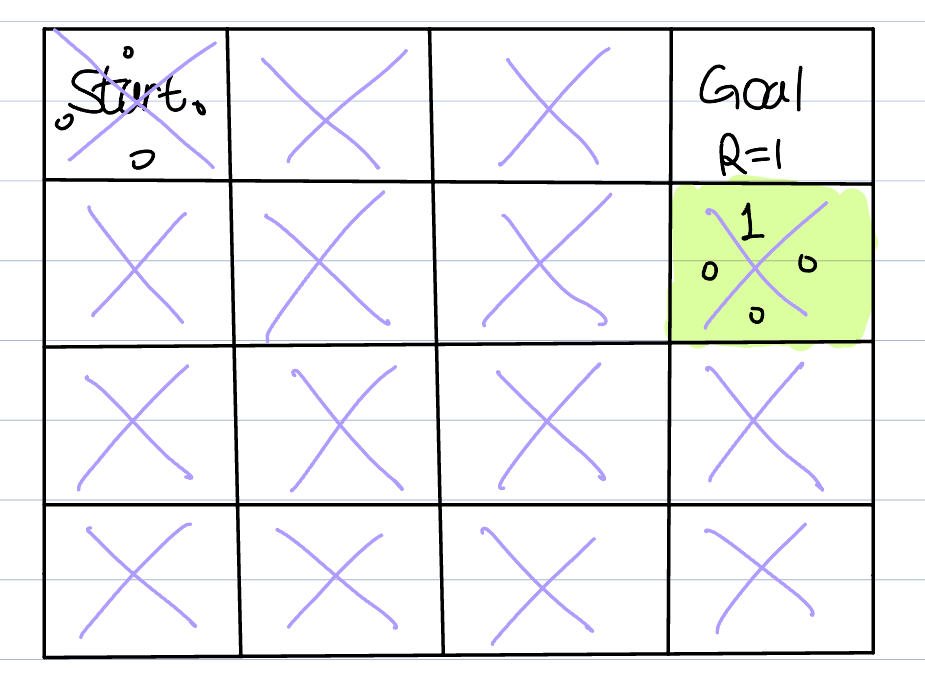
We then update the green box's s1 score to 1. The first episode is over, and we move on to the second episode. The agent has all zero score at the start, it moves randomly again. Then, when it reaches the green box and assume that the agent visited the yellow box just before the green box, we update yellow box's s3(right) score to the largest value in the green box(it is 1).

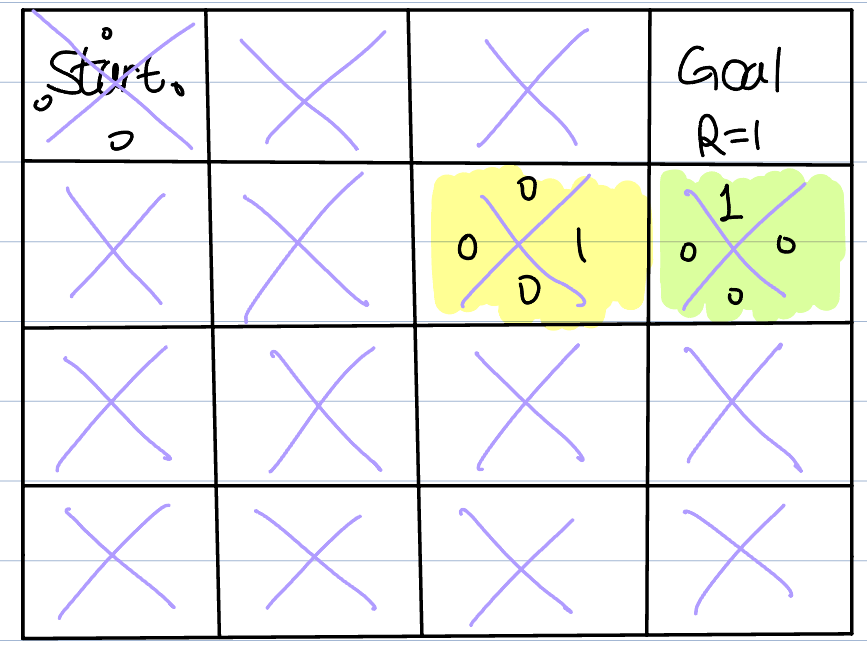
This process is repeated until the agent finds 'the path'.

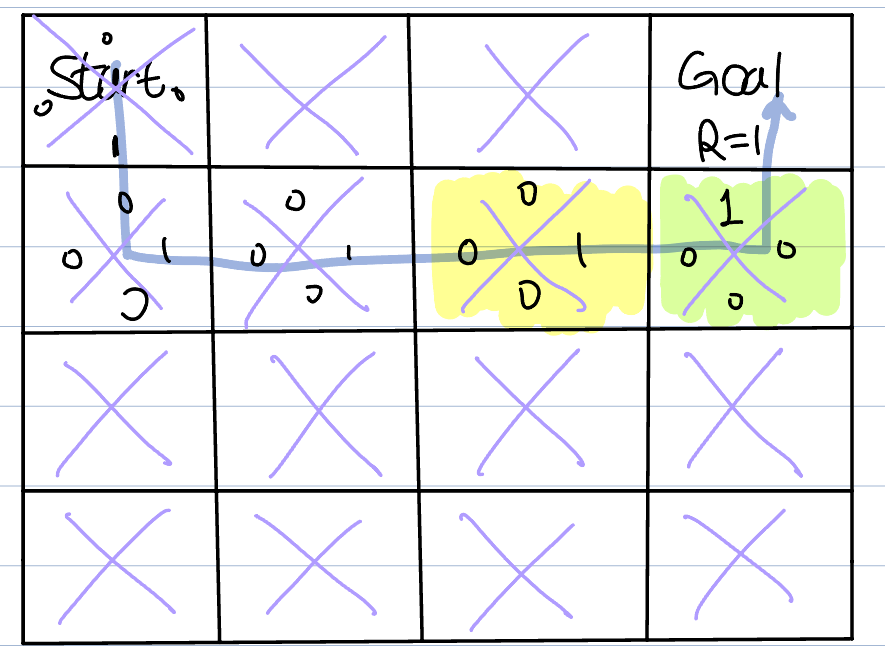
The agent has found the path but it seems not perfect(It is not the shortest path!). Therefore, we introduce a new concept : exploration and exploitation. To explore, the agent do $\varepsilon$ - greedy action. We can freely assign $\varepsilon$ a value between 0 and 1. $\varepsilon$ of the agent moves randomly, and the rest moves in the direction of the maximum score. Exploration is to move randomly, and exploitation is to move in the direction of the maximum score. If $\varepsilon$ is 0, then it is just exploitation(no changes). In contrast, if $\varepsilon$ is 1, then the agent moves only randomly(exploration). Therefore, they are in a tradeoff relationship.

The exploration has two advantages. One is that it can find a new path(could be the shortest!). Another is that it can find a new goal. The above example has only one goal, but there could be multiple goals. This advantage is important because the new goal might have greater reward than original goal.

To find an appropriate tradeoff, we introduce decaying $\varepsilon$-greedy action. We first define $\epsilon$ as high value(like 0.9) and we make $\epsilon$ 0 as the episode progresses.
After exploration, the agent might have found a new path.

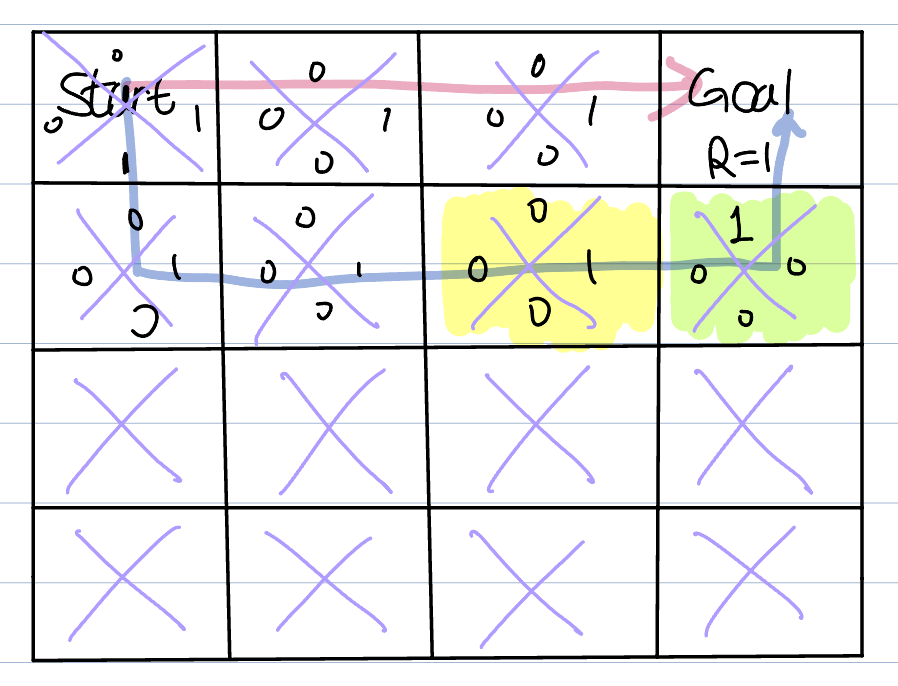
But the problem is that every path has the same score(the maximum value is 1). The agent does not know which path is better.
Therfore, we apply mathematic techniques : discount factor.
The discount factor is denoted as $\gamma$ (0 ~1).
Now, we update current box’s score by getting the maximum value(multiplied by $\gamma$) in the next box of the path.
It may be easy to understand the concept by figure.

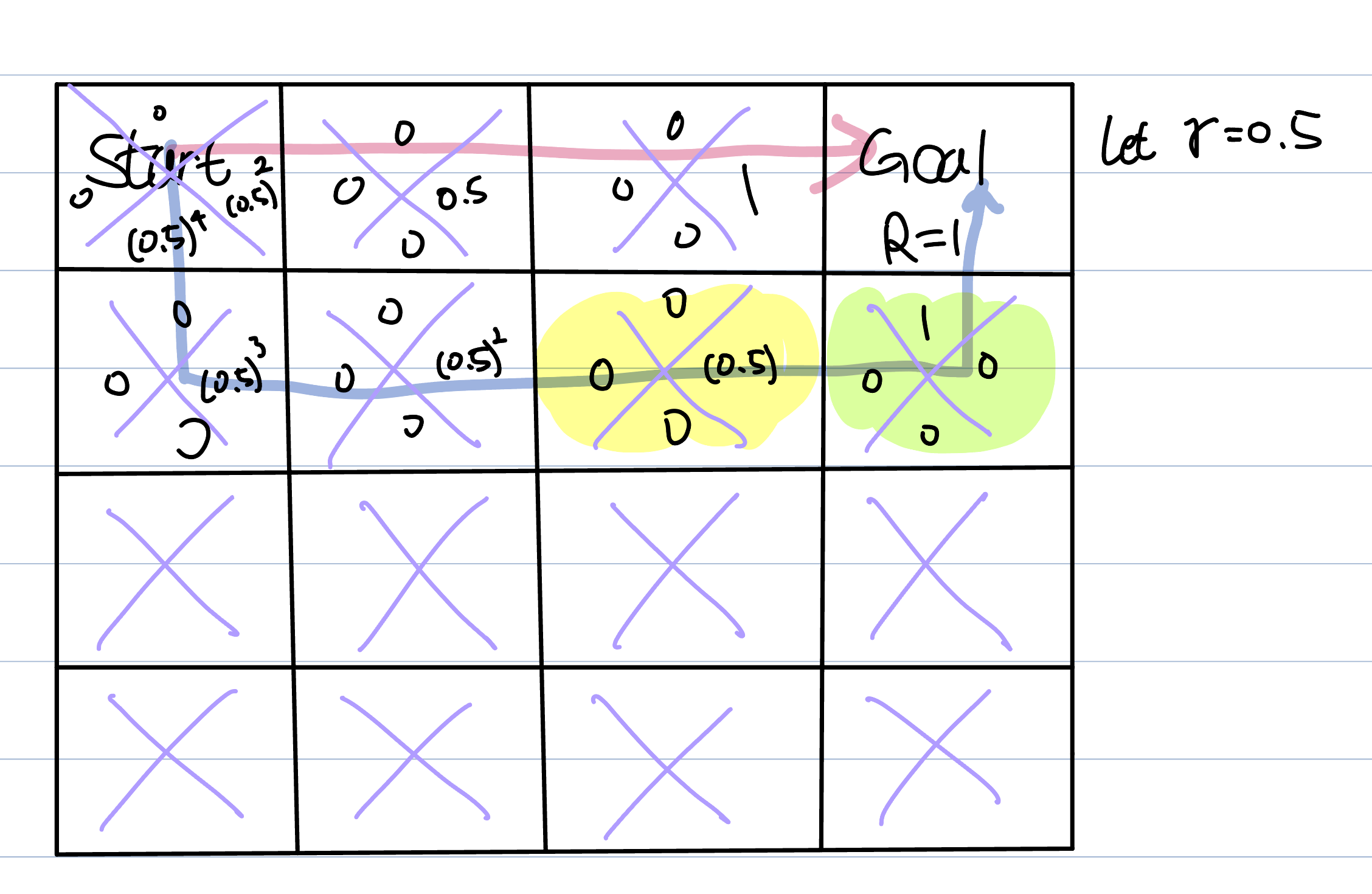
Since the agent moves in maximum value direction, it can now follows to the shortest path!

If the discount factor is near zero, the agent becomes insensitive to future rewards. We can decide where the agent should focus(future or present).

Q- update

To be specific on the updating scores, we do not just get (maximum value $\times \gamma$).
We first define current state as $Q(s_t, a_t)$.
Then, the next state(next box) will be $Q(s_{t+1}, a_{t+1})$
The $a_t$ stands for the action.(up / down / right / left).
The $s_t$ stands for the agent’s location(which box).

The state Q is updated by the following equation.
$Q(s_t, a_t) \leftarrow (1-\alpha)Q(s_t, a_t) + \alpha(R_t + \gamma \max\limits_{a_{t+1}} Q(s_{t+1}, a_{t+1}))$
$R_t$ stands for the reward(If the next box is not the goal, the $R_t$ is 0).
$\alpha$ is between 0 to 1.
$\max\limits_{a_{t+1}}$ means that finding the action($a_{t+1}$) which has the largest value in the next box.
The point is, $(1-\alpha)Q(s_t, a_t)$ is 0 to every box in the first episode. This term affects after the first episode.

In short, the equation means that, we update q by multiplying its original value by 1-$\alpha$ and adding the largest score in the next box multiplied by $\alpha$.

As the value of $\alpha$ increases, we increase the weight of the second term. -> $\alpha$ determines how much a new value is accepted.