2-1. Markov Decision Process(MDP)

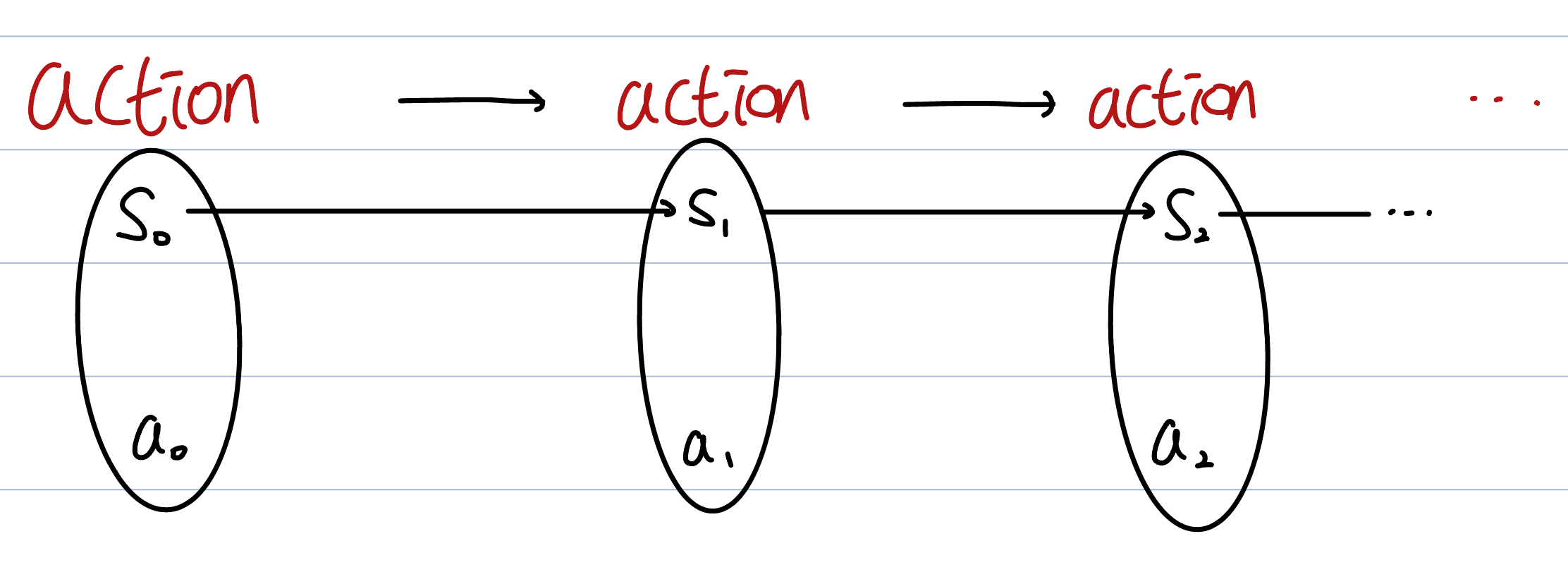
What is MDP?

Decision means, the agent decides what action to take in each state.

Every action($a_t$) leads to next state($s_t$).

The first important properties of MDP is that every action is done randomly. This means state and action has (discrete) probability distribution.
$p(a_1 | s_0, a_0, s_1)$
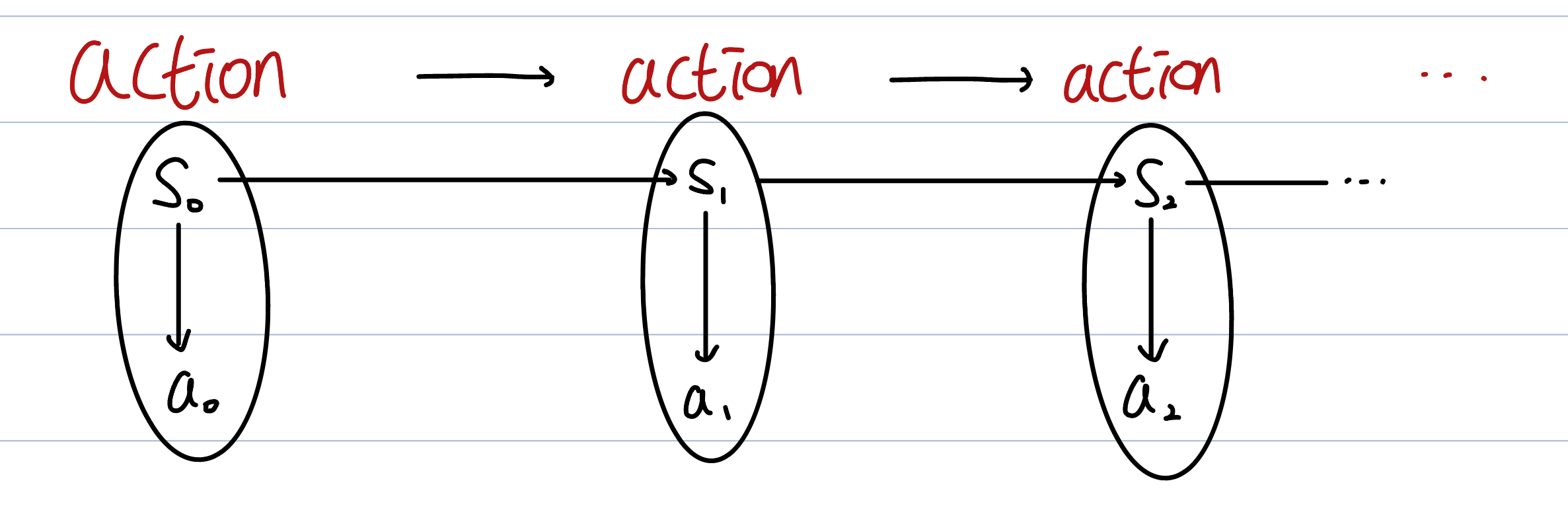
The arrows shown in the figure represent the information needed to find the probability distribution of the random variable.
So if we know the information of $s_1$, then we don’t need $s_0, s_1$ anymore.(The probability distribution becomes $p(a_1 | s_1)$). This is because $s_1$ already has the information about $s_0$ and $a_0$.

On the same principle, we can simplify the distribution of $s_2$.
It first represented as $p(s_2|s_0,a_0,s_1,a_1)$.
Since $s_1$ already has the information about $s_0, a_0$, we do not need anymore. Therefore we need $s_1, a_1$ to decide the distribution of $s_2$.
$p(s_2|s_1,a_1)$

Policy

We know how to represent the probability distribution about each state and action. The probability distribution of the action is called Policy. Since the agent has information about current state, and prior states, instructions on what action to take are expressed as a probability distribution.

The goal of reinforcement learning is to maximize reward. To be specific, the agent tries to maximize expected return.
Return can be expressed in a formula as follows:
$G_t \triangleq R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + …$
The formula means the return is sum of the discounted reward. ($\gamma$ is the discounted factor as we learned in Q-learning)
Let’s recall the Q-learning.

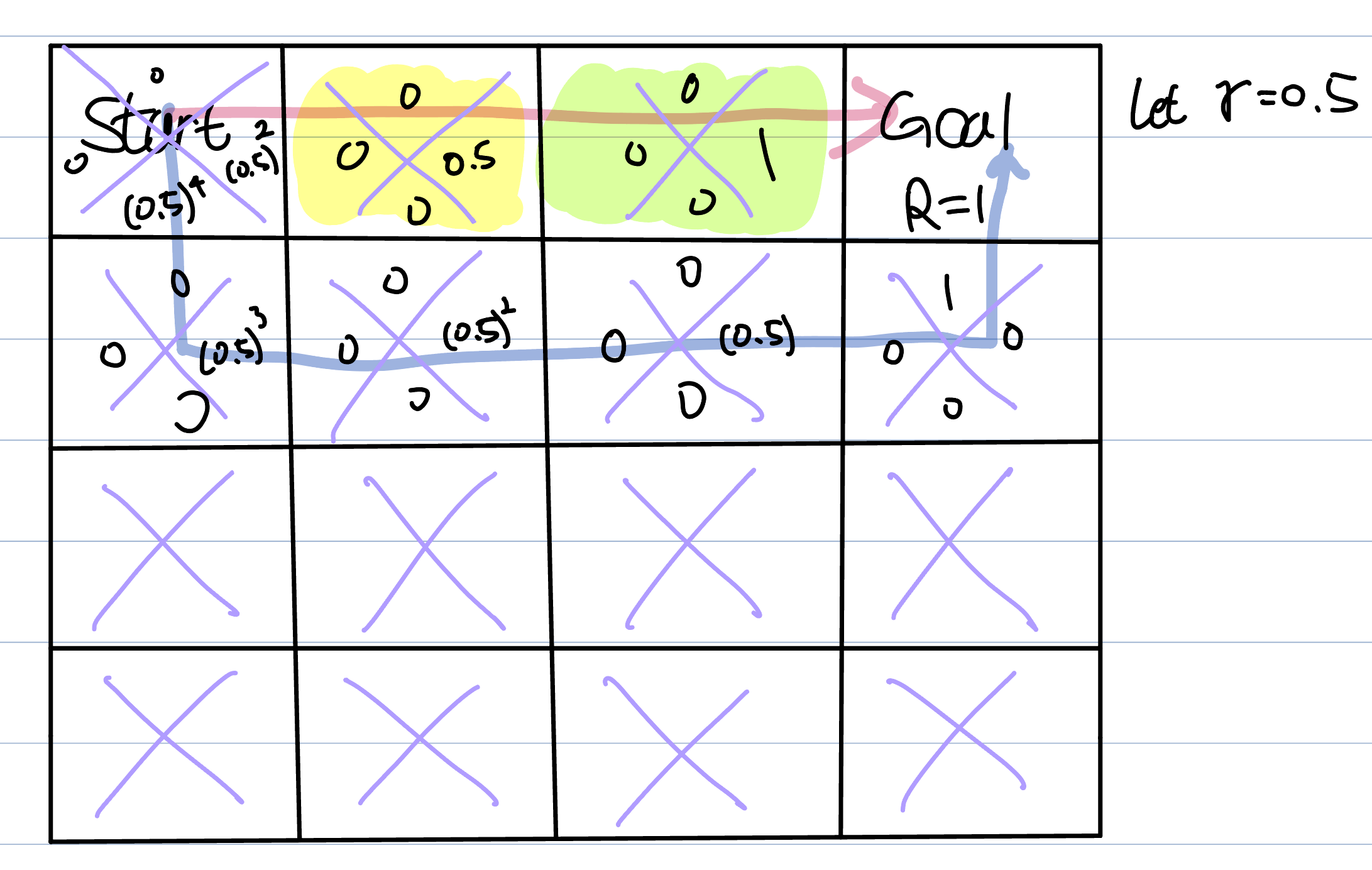
Look at the yellow box. The return of this box is 0.5. Since the next box do not have any reward, $R_t$ becomes 0. The only return is $\gamma R_{t+1}$.
In contrast, the return of the green box is $R_t = 1$(because the next box is goal).

The agent acts randomly -> next state and reward is random as well.
$\therefore$ we need expected reward.
The policy forces the agent to maximize average of random rewards.

In conclusion, Markov Decision Process is to find the optimal policy that maximizes the expected return.