3. Introduction to vector calculus and partial derivatives

Neural Network의 layers는 $f(x)$와 같이 하나의 파라미터를 가진 하나의 function이 아니다. 따라서, 여러 개의 파라미터를 가진 함수 $f(x,y)$를 보자.
예를 들어, $xy$의 미분은 무엇인가? (즉, $x$와 $y$의 곱의 미분은 무엇인가?)

다시 말하면, 변수가 달라지면, $x$와 $y$의 곱은 어떻게 달라지는가? 이것은 우리가 $x$와 $y$를 어떻게 바꾸는가에 달려있다.
이제까지 우리는 한번에 하나의 변수(parameter)만 미분하였다. 우리에게 2개의 파라미터를 가진 함수가 주어지면, 'partial derivatives'(편미분)를 사용하면된다. 한번에 변수 하나씩을 미분하는 것이다.
$\frac{d}{dx}$를 사용하는 대신, 라운드 d를 사용하여 다음과 같이 나타낸다.
라운드 d: ∂ 라고 쓴다. $\delta$, $d$와는 다른 문자이다.

$\frac{∂}{∂ x}$

$xy$의 편미분은 $\frac{∂}{∂x}xy$, $\frac{∂}{∂y}xy$ 라고 쓸 수 있다. 이것들을 partials 라고 부른다.

single parameter에 대한 functions에서, $\frac{∂}{∂ x}$는 $\frac{d}{dx}$와 같다. 하지만, single parameter가 있는 함수에서는 $\frac{d}{dx}$를 사용하는 것이 scalar 미분을 말할 때 더 명확하기 때문에 d라고 쓰는 것을 권장한다.

$x$에 대한 편미분은 일반적인 scalar 미분으로 계산한다. 함수의 다른 변수는 상수로 처리하여 계산한다.

다음 함수를 보자.
$f(x,y)=3x^2y$

x에 대한 미분

$x$에 대한 편미분을 다음과 같이 쓸 수 있다.
: $\frac{∂}{∂x}3x^2y$
위의 식에서 3, 2, y 는 상수(constants)로 처리한다.
$\frac{∂}{∂x}3x^2y = 3x^2\frac{∂}{∂x}y = 3y2x = 6yx$

y에 대한 미분

$y$에 대한 편미분을 다음과 같이 쓸 수 있다.
: $\frac{∂}{∂y}3x^2y$
위의 식에서 3, 2, x 는 상수(constants)로 처리한다.
$\frac{∂}{∂x}3x^2y = 3x^2\frac{∂}{∂x}y = 3x^2\frac{∂}{∂x} = 3x^2 \times 1 = 3x^2$

계속 이 자료를 읽기 전에 이러한 전개를 직접 해보는 것이 좋다. 그렇지 않으면 나머지 부분을 읽어도 의미가 없다. 이해가 어렵다면 칸 아카데미의 비디오를 참고하여라.

우리는 다변수 미적분뿐만 아니라, 벡터 미적분을 하고 있다.
$f(x,y) = 3x^y$를 미분하기 위해 다음 2개의 편미분 $\frac{∂f(x,y)}{∂x}$와 $\frac{∂f(x,y)}{∂y}$ 을 고려한다.

$f(x,y)$의 gradient 를 다음과 같이 적을 수 있다.

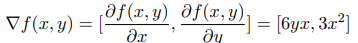
위의 식에서 $f(x, y)$의 gradient는 단순히 편미분의 벡터(a vector of its partials) 라고 할 수 있다. gradient는 n개의 scalar parameters를 single scalar에 매핑하는 함수를 다루는 벡터 미적분의 일부이다.

자! 이제부터 여러 함수의 편미분을 동시에 다뤄보자! -> Chapter 4에서 계속!

Reference

• The Matrix Calculus You Need For Deep Learning