생성 모델의 이론적 이해

이 포스팅에서 LLM, 이미지 생성 모델(GAN, AutoEncoder, Diffusion 등)들을 살펴보았다. 이번에는 생성 모델의 이론적인 부분을 공부해보자.

Statistical generative models

우리가 이미지 등의 데이터를 생성하기 위해 모델에 방대한 양의 prior knowledge(physics, materials, ...)를 전부 넣는 것은 불가능하다. 그래서 보통의 생성 모델은 기존 데이터의 분포를 학습하여 새로운 데이터를 생성하게 되고, 이를 statistical generative model이라고 한다. statistical generative model은 데이터로부터 paramteric form (ex) Gaussian, ...)을 추정하고 loss function, optimization algorithm를 이용하여 실제 데이터와의 차이를 줄여 현실과 가까운 데이터를 생성한다.

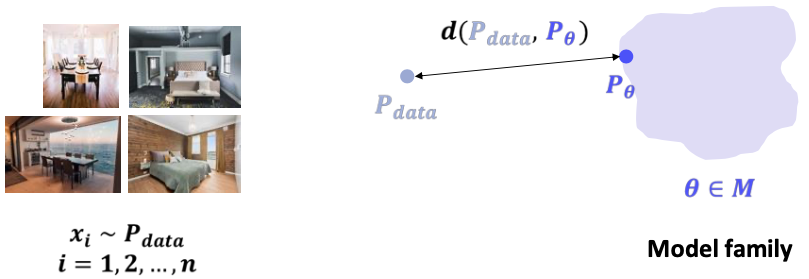
statistical generative model은 크게 1) 데이터, 2) model family, 3) 거리 함수, 4) 최적화 방법론으로 구성된다.

• 데이터
• model family : 데이터에서 추출한 parametric form을 만족하는 모델들의 집합
• 거리 함수 : 주어진 데이터와 그를 바탕으로 만들어진 모델 사이의 차이
• 최적화 방법론 : 거리 함수를 줄여 입력된 데이터와 가장 유사한 모델을 찾기 위한 알고리즘

동작 원리

일반적인 분류 모델은 데이터를 입력받아 데이터의 class를 판별하고 그 class에 속할 확률, 즉 conditional probability distribution을 계산한다. (→ $P(Y=dog|X=input\, image)$)

하지만 생성 모델은 데이터를 입력받는 것이 아니라 생성하는 모델이다. 생성 모델은 (X = 생성된 이미지)와 (Y = class)의 joint probability distribution을 학습한다. (→ $P(X = generated\, image, Y=dog)$) 예를 들어 생성된 이미지가 개일 때 class가 dog일 확률은 크도록, 생성된 이미지가 고양이일 때 class가 dog일 확률은 작도록 학습하는 것이다.

* joint probability distribution : 여러 변수들의 값이 동시에 특정 값을 가질 확률. P(X=a, Y=b)는 X라는 변수가 a라는 값을 가지는 동시에 Y라는 변수가 b라는 값을 가질 확률이다. (ex) 주사위 A에서 2, 주사위 B에서 5가 나올 확률)

conditional probability의 정의에 따르면 생성모델이 학습한 joint probability로부터 분류 작업도 할 수 있다.

$P(Y|X) = \frac{P(X, Y)}{P(X)} = \frac{P(X \cap Y)}{P(X)}$

생성 모델은 $P(X, Y)$를 학습하여 알고 있기 때문에 $P(X)$를 구한다면 이미지가 주어졌을 때 어떤 클래스에 속할 확률 $P(Y|X)$를 알 수 있다. 그러나 $P(X)$는 데이터의 분포로, 이 분포를 정확히 구하기 어렵기 때문에 생성모델을 바탕으로 한 분류 작업은 작동하기 어렵다. 하지만 $P(X)$를 잘 구할 수 있다면, 이미지가 크게 손상되었을 때 작동하지 않는 분류 모델에 비해, 생성 모델은 손상된 이미지로도 어느 정도 확률을 구할 수 있다.

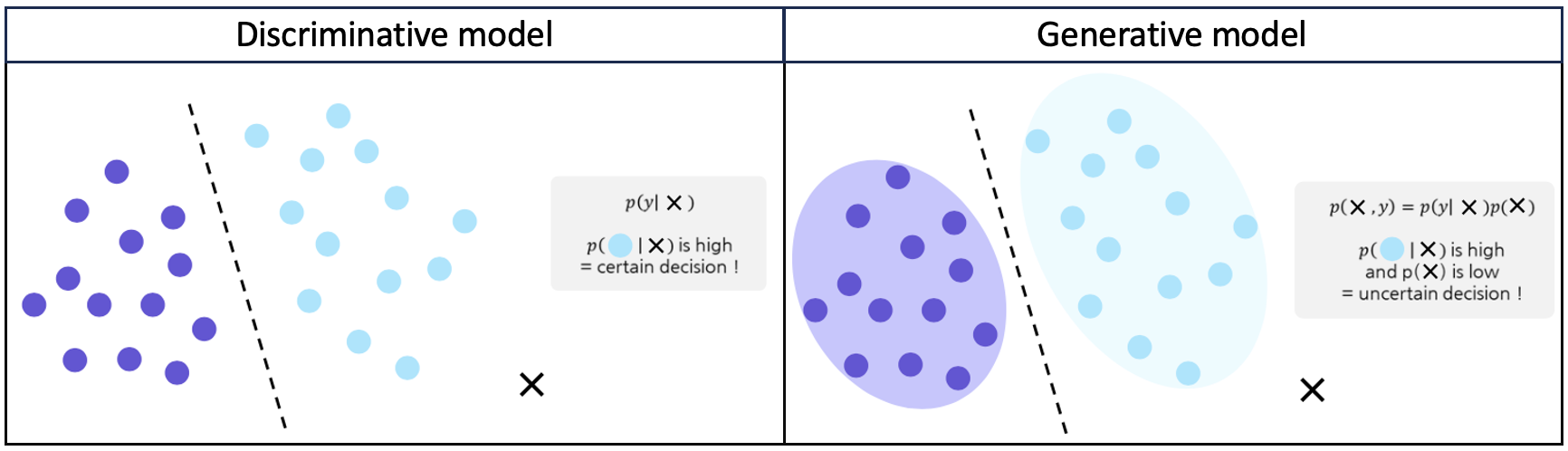
또한 $P(X)$를 잘 구할 수 있다면 생성 모델이 outlier를 고려한 더 정확한 분류를 할 가능성도 있다. 위 그림의 왼쪽 분류 모델을 보면, 새로운 데이터 $\times$가 들어왔을 때, 단순히 decision boundary의 오른쪽에 있기 때문에 하늘색 포인트와 같은 클래스로 분류될 것이다. 하지만 생성 모델은 데이터의 분포 $P(X)$까지 고려하여 분류를 하게 되기 때문에 $\times$가 decision boundary의 오른쪽에 있더라도 기존 데이터의 분포와 차이가 나는 것을 고려하여 outlier로 규정할 수 있게 된다.

학습 방법

Maximum likelihood learning

Maximum likelihood learning은 데이터를 가장 잘 설명하는 모델 파라미터를 찾는 방법이다. 주어진 데이터가 모델에서 나올 확률을 최대화하는 방식으로 자연스러운 데이터 생성을 유도한다.

$max_{P_\theta} \frac{1}{|D|} \sum log P_{\theta}(x)$

이 방식으로 학습한 모델이 Latent Variable Model(은닉 변수가 있는 모델)이다. 위에서 언급했듯 $P(X)$는 구하기 쉽지 않다. 하지만 여기에 z라는 latent variable을 도입하면 $P(X)$를 더 잘 근사할 수 있다. 보통 X는 multivariate해서 복잡하지만 여기에 우리가 알고 있는 z로 conditional probability $P(x|z)$를 계산하면 보다 단순한 분포가 된다. 그래서 여러 변수에 대해 이 conditional probability를 계산하여 합치면 복잡한 $P(X)$도 보다 간단하게 근사할 수 있는 것이다. z를 모를 경우에는 데이터로 학습해서 구할 수 있다.

z를 구하는 과정을 구체적인 예로 살펴보도록 하자. 위는 MNIST 손글씨 숫자 이미지 데이터인데, ?로 가려진 부분이 latent한 부분 z이다. 이 상태에서 전체 X를 정확히 알기 위해서는 $\sum_z p(x, z; \theta)$를 계산해야 한다. 그러나 이는 직접적으로 계산하기 매우 어렵기 때문에 근사하는 방식으로 접근해야 한다.

$\sum_z p(x, z; \theta)$를 근사하기 위한 첫 번째 방법으로는 Monte Carlo가 있다. $p_{\theta}(x)$의 계산 과정을 수학적 트릭을 이용해서 정리하면 아래와 같이 되는데, 이는 z가 uniform distribution으로 분포한다는 의미가 된다.

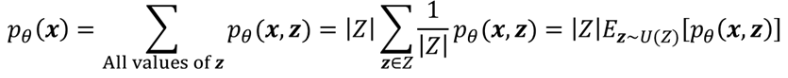
따라서 Monte Carlo 샘플링으로 계산할 수 있게 된다. 그러나 Monte Carlo 특성상 무수히 많은 랜덤한 포인트에 대해 계산을 해야 하므로 보다 효율적인 방법을 찾는 것이 좋다.

이런 점을 보완하고자 한 것이 Importance Sampling이다. 위 데이터에서 무작위로 z를 샘플링하지 않고, 가운데 부분이 흰색 (숫자 부분), 가장 자리 부분이 검은 색 (배경)일 확률이 크기 때문에 이러한 점을 고려해서 샘플링하는 것이다. 마찬가지로 수학적 트릭을 이용해 식을 다시 정리하면 q(z)라는 중요도를 반영한 확률 분포에서 z를 샘플링할 수 있다. 여기에 Monte Carlo를 이용해 계산하면 첫 번째 방법보다 효율적으로 $\sum_z p(x, z; \theta)$를 근사할 수 있게 된다.

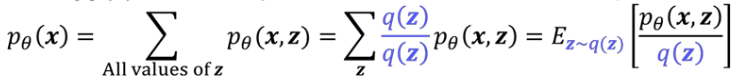
그러나 샘플링을 반복하며 계산하기 때문에 상당히 느리고, q(z)의 설정에 따라 성능이 달라질 수 있기 때문에 주의가 필요하다.

그래서 가장 적절한 q(z)를 설정하기 위해 Variational Inference 방법이 고안되었다. 이는 posterior probability $p(z|x;\theta)$를 이용하는 방법인데, 저 숫자가 8이다 라는 선험적 지식을 바탕으로 z가 무엇인지 추정하는 것이다. 그러나 $p(z|x;\theta)$도 여전히 구해야하는 값이다. 이전의 Importance Sampling 방식이 중요도를 기반으로 Monte Carlo 계산ㅇ르 했다면, 여기서는 적절한 최적의 q(z)를 구하기 위해서 q(z)와 $p(z|x)$의 차이를 최소화하는 optimization problem으로 바꿔서 생각한다. 두 분포의 차이는 KL divergence를 이용해 구할 수 있으므로 이 최적화 문제를 이용해 최적의 q(z)를 찾는다.

$q^*(z) = arg\, min\, KL (q(z)|p(z|x))$

그러나 사실 우리는 $p(z|x)$를 모른다. 그래서 다른 표현을 이용해보고자 식을 전개하면 아래와 같다.

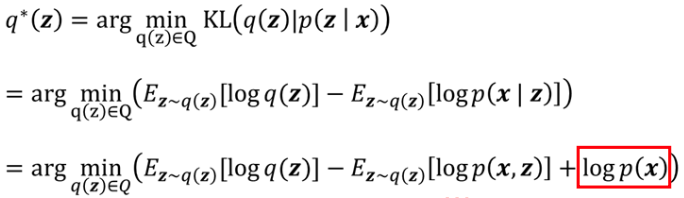
그러나 이 역시 우리가 정확히 알지 못하는 $p(x)$가 포함되어 있는 것을 볼 수 있다. 이 문제를 해결하기 위해 ELBO (Evidence Lower BOund)라는 트릭을 사용한다. (중간 과정 생략...) 그러면 $log\, p(x)$의 lower bound를 구할 수 있게 되고, q(z)와 $p(z|x)$의 분포가 같을 때에는 등식도 될 수 있다.

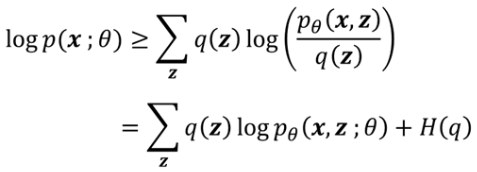
(ELBO에 대한 자세한 해석은 생략...)