정답 데이터 없이 학습하는 비지도 학습의 주요 알고리즘 중 하나는 clustering (군집화) 이다. clustering은 특징이 비슷한 데이터들끼리 무리를 짓도록 분류하는 기법이다. clustering에는 K-Means, DBSCAN, Hierarchical Clustering 등의 방법이 있다.
K-Means
K-Means는 주어진 데이터를 k개의 그룹으로 나누는 알고리즘이다. 가장 먼저 데이터를 몇 개(k)의 그룹으로 나눌 것인지 k 값을 정하고, 그 그룹들의 중심 위치(centroid)가 어디일지 정한다. 그러면 모든 데이터들에 대해 각 그룹의 centroid까지의 거리를 계산하여 가장 거리가 가까운 그룹으로 분류한다. 이렇게 1차적으로 분류된 그룹에 대해서, centroid를 초기의 위치에서 그룹의 중심으로 옮긴다. 그리고 다시 같은 방식으로 분류한 후 그룹이 다시 배정되는 데이터가 없을 때까지 이를 반복한다. K-Means는 scikit-learn으로 구현된 것을 이용할 수 있다.
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from matplotlib import pyplot as plt
import numpy as np
# make_blobs : 가우시안 분포를 이용해 임의의 데이터를 생성한다. 보통 군집화 가상 데이터를 생성하는데 사용된다.
coord, label = make_blobs(n_samples=500, centers=4, cluster_std=0.6, random_state=1)
# coord = 데이터의 좌표
# label = 데이터의 그룹 정보
# 우선 만들어진 데이터들의 좌표 상의 분포를 확인해보자.
plt.scatter(coord[:,0], coord[:,1], s=5, c='grey')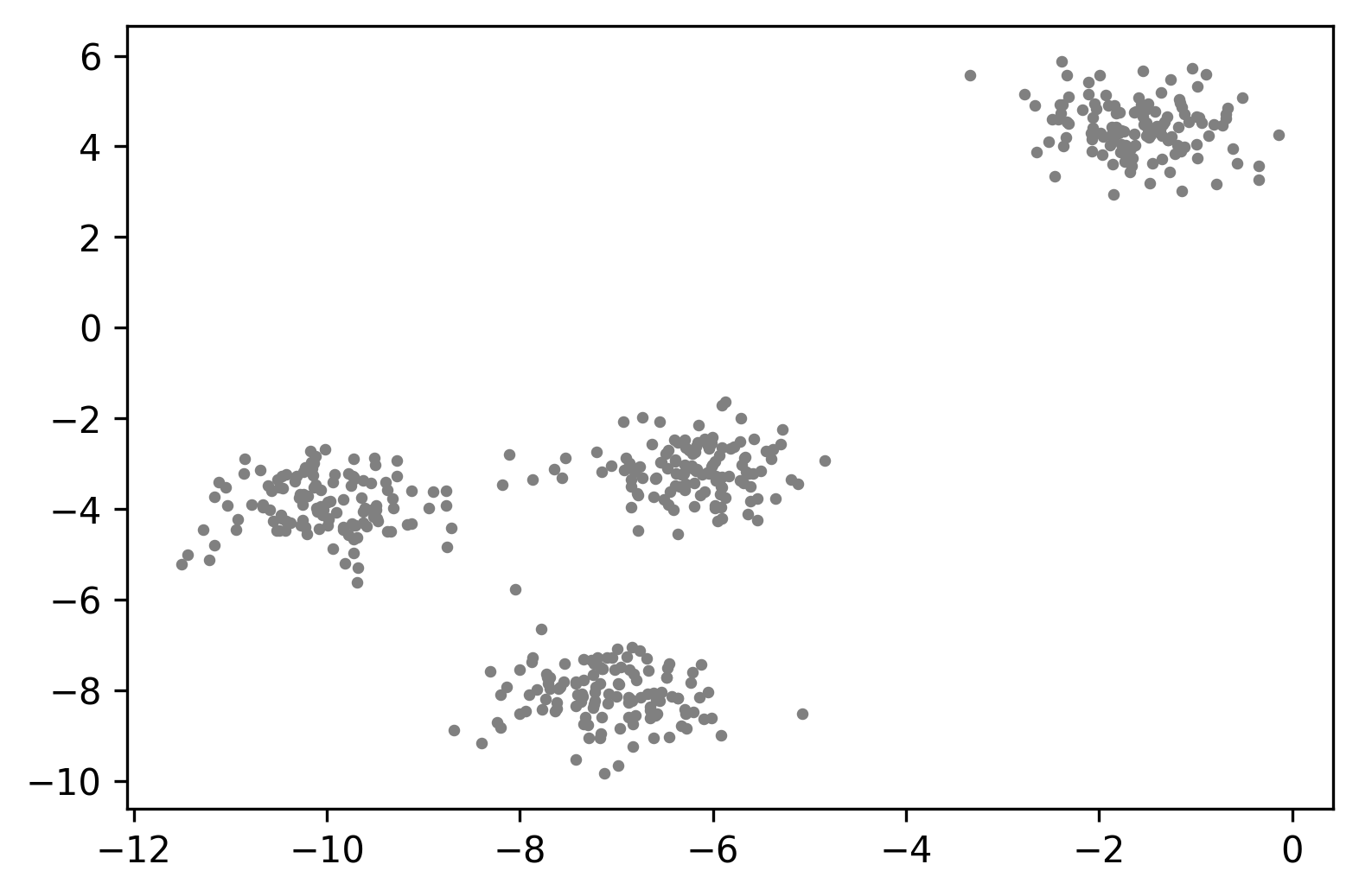
# K-Means를 이용한 데이터의 군집화
# 4개의 그룹으로 분류하자.
kmeans = KMeans(n_clusters=4)
label_predicted = kmeans.fit_predict(coord)
# 잘 clustering 되었는지 시각적으로 확인하기
plt.scatter(coord[:,0], coord[:,1], s=5, c=label_predicted, cmap='jet')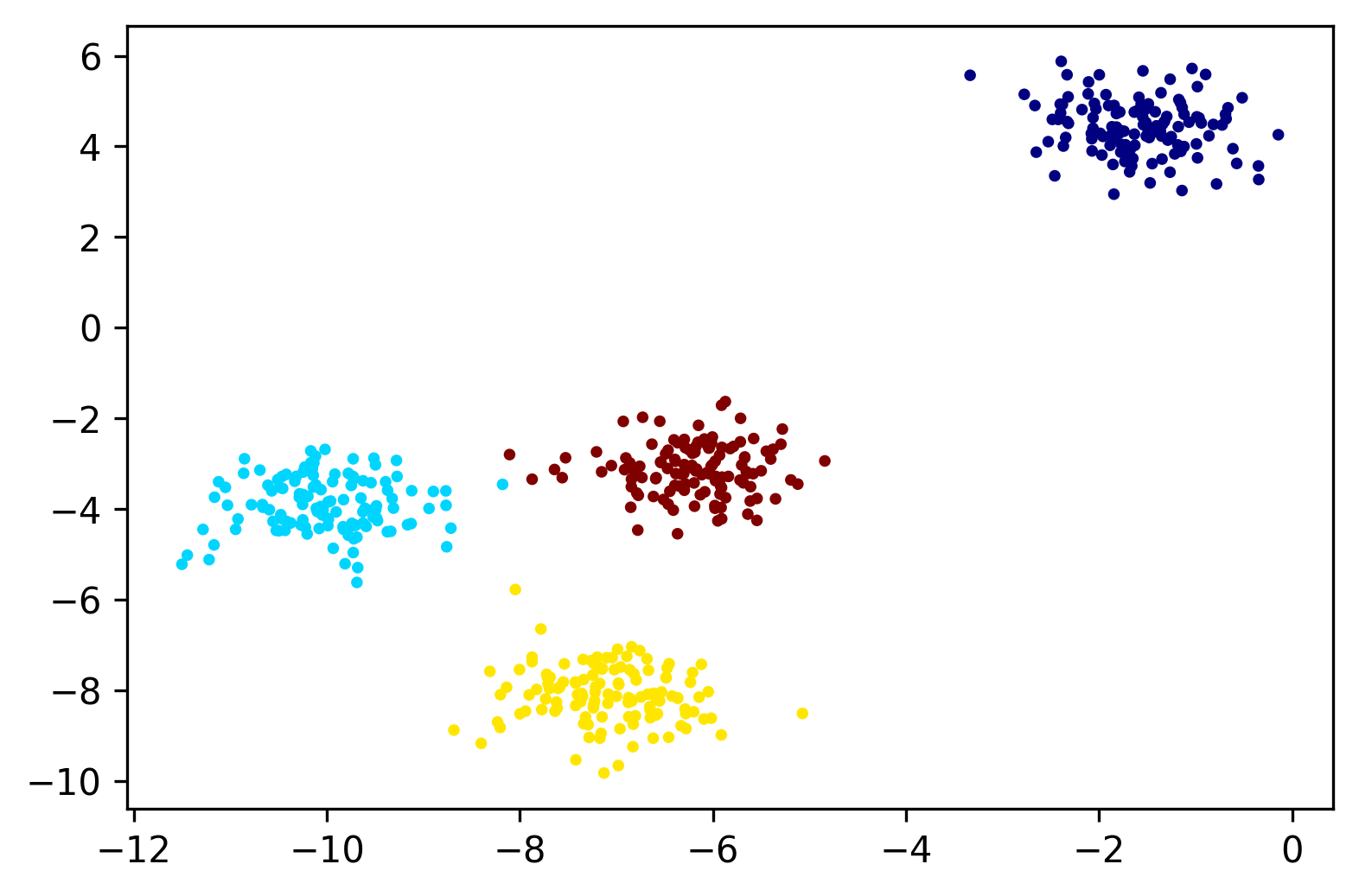
위의 그림을 통해 대략적으로 clustering이 잘 된 것을 확인할 수 있다. 엄밀하게 확인하고자 하는 경우, label과 label_predicted를 비교해보면 될 것이다.
그러나 보통은 데이터가 몇 개의 그룹으로 나누어질지 알 수 없는 경우가 대부분이다. 이 때 inertia value를 이용해 k 값을 미리 추정할 수 있다. inertia value는 clustering 작업이 끝난 후, 각 centroid에서 그룹으로 분류된 데이터 간의 거리를 합산한 값이다. 즉, inertia value가 작을수록 clustering이 잘 되었다고 판단할 수 있다. 따라서 가능한 inertia value의 범위를 정해 반복문으로 테스트를 해보고, inertia value가 일정 값으로 수렴하면 그 값을 전후해 k 값을 정하면 된다.
# inertia value 추정하기
k_list = range(1, 10)
inertia_values = []
for k in k_list:
kmeans = KMeans(n_clusters=k)
kmeans.fit(coord)
interita_values.append(kmeans.inertia_)위에서 계산한 k 값에 따른 inertia value를 그림으로 그려보면 아래와 같다.
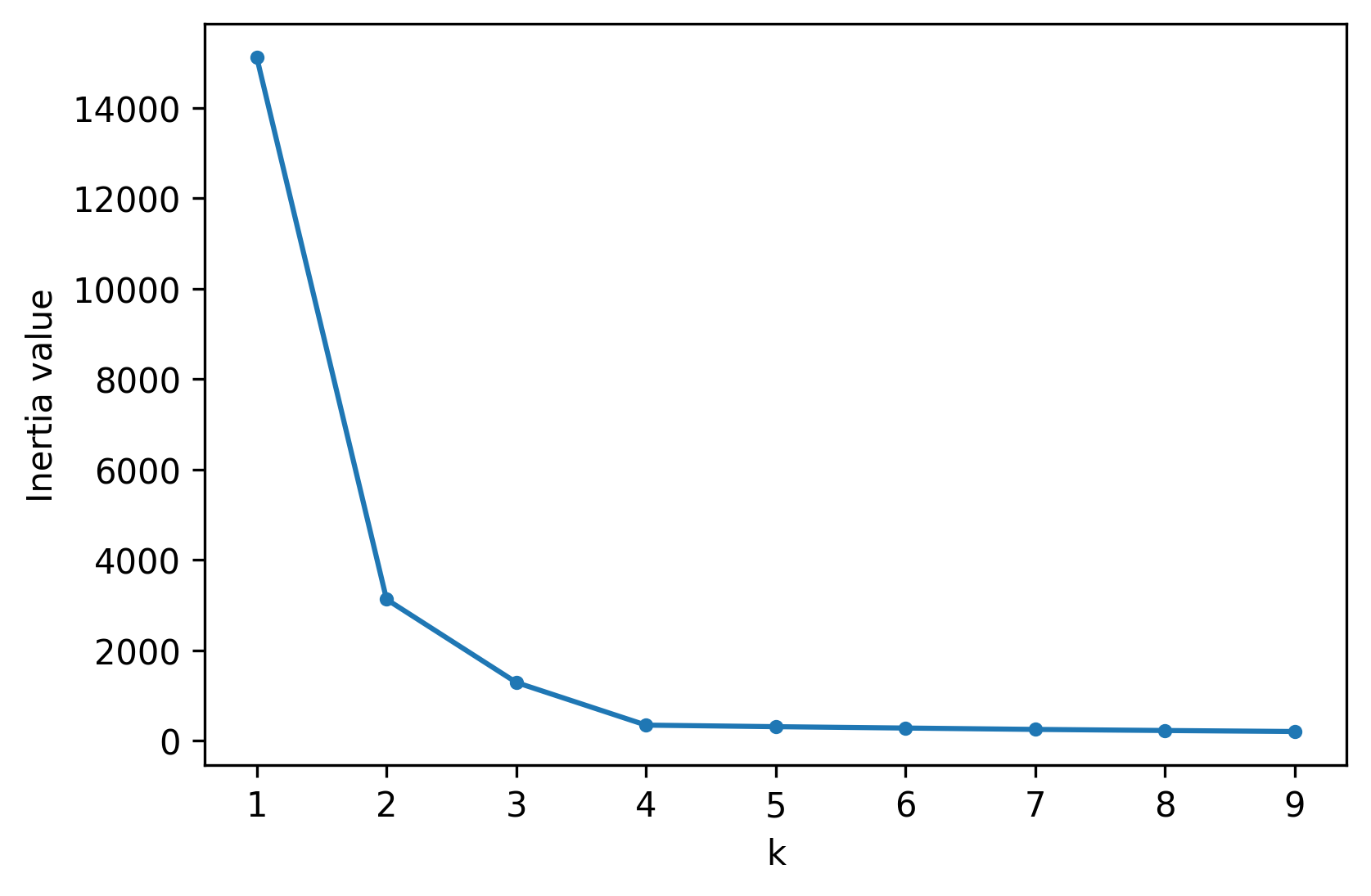
이 경우 대략 k = 4부터 일정 값으로 수렴하고 있기 때문에 k = 4 를 선택하는 것이 적절할 수 있다.
이렇듯 K-Means는 k를 사전에 정해줘야 하고, 초기 centroid를 랜덤하게 결정하기 때문에 이로 인해 잘못 분류될 위험이 있다.
K-Means++
초기 centroid의 위치를 보다 신중하게 설정해서 기존의 K-Means의 단점을 보완하는 방법이 K-Means++이다. 알고리즘은 K-Means와 동일하되, 데이터 중 하나를 랜덤하게 선택해서 그 데이터를 초기 centroid로 설정한다는 점이 다르다. 그 후 centroid와 다른 데이터들 사이의 거리를 계산하고, 그 중 가장 멀리 있는 데이터를 다음 centroid로 설정하고, 이 과정을 k개의 centroid가 지정될 때까지 반복한다. K-Means++는 scikit-learn의 KMeans에서 init 옵션을 'k-means++'로 설정하면 된다.
kmeansplus = KMeans(n_clusters=4, init='k-means++')
label_predicted1 = kmeansplus.fit_predict(coord) Hierarchical clustering
Hierarchical clustering(계층적 군집)은 가장 작은 단위의 데이터부터 비슷한 데이터들끼리 군집화를 시작해서 최종적으로 하나의 그룹이 될 때까지 반복하여 그룹짓는 알고리즘이다. scikit-learn의 AgglomerativeClustering 기능이 hierarchical clustering을 구현해 놓았다.
from sklearn.cluster import AgglomerativeClustering
label_hc = AgglomerativeClustering(n_clusters=4).fit_predict(coord)
# 시각화로 확인해보기
# K-Means로 clustering한 것과 약간 다른 결과가 나올 수 있다.
plt.scatter(coord[:,0], coord[:,1], s=5, c=label_hc, cmap='jet')DBSCAN
DBSCAN (Density-Based Spatial Clustering of Applications with Noise; 밀도 기반 군집화) 은 데이터의 밀도를 기반으로 군집화를 하는 알고리즘이다. 특정 반경 내에 데이터가 n개 이상 있으면 한 그룹으로 묶는다. 특히, 데이터의 공간적 분포가 기하학적인 모양으로 나타날 때에도 군집화를 잘 해준다. scikit-learn의 DBSCAN으로 알고리즘이 구현되어 있다.
from skleran.cluster import DBSCAN
# eps = 두 데이터를 하나의 그룹으로 묶는 최대 거리
# min_sample = 그룹으로 묶이는 (특정 반경 내) 샘플의 최소 개수
label_dbscan = DBSCAN(eps=0.6, min_samples=5).fit_predict(coord)
# 시각화로 확인해보기
# 다른 방법으로 clustering한 것과 약간 다른 결과가 나올 수 있다.
plt.scatter(coord[:,0], coord[:,1], s=5, c=label_dbscan, cmap='jet')"데이터의 공간적 분포가 기하학적인 모양으로 나타날 때"의 경우를 다른 clustering 알고리즘의 결과와 비교해보도록 하자. scikit-learn의 make_moons 함수를 이용하면 초승달 모양 (=arc) 으로 분포하는 데이터를 생성할 수 있다.
from sklearn.datasets import make_moons
coord1, label1 = make_moons(500, noise=0.05, random_state=1)
# K-Means++ vs DBSCAN
# K-Means++
label_kplus = KMeans(n_clusters=2, init='k-means++').fit_predict(coord1)
# DBSCAN
label_dbscan1 = DBSCAN(eps=0.3, min_samples=5).fit_predict(coord1)
# 시각화로 비교해보기
fig, ax = plt.subplots(1, 2, dpi=300, figsize=(10,4), constrained_layout=True)
ax[0].scatter(coord1[:,0], coord1[:,1], s=10, c=label_kplus, cmap='prism')
ax[0].set_title('K-Means++')
ax[1].scatter(coord1[:,0], coord1[:,1], s=10, c=label_dbscan1, cmap='prism')
ax[1].set_title('DBSCAN')위 코드를 실행해보면 DBSCAN이 다른 clustering 알고리즘에 비해 기하학적 분포를 가진 데이터를 군집화하는 것에 강점을 가지는 것을 알 수 있다.
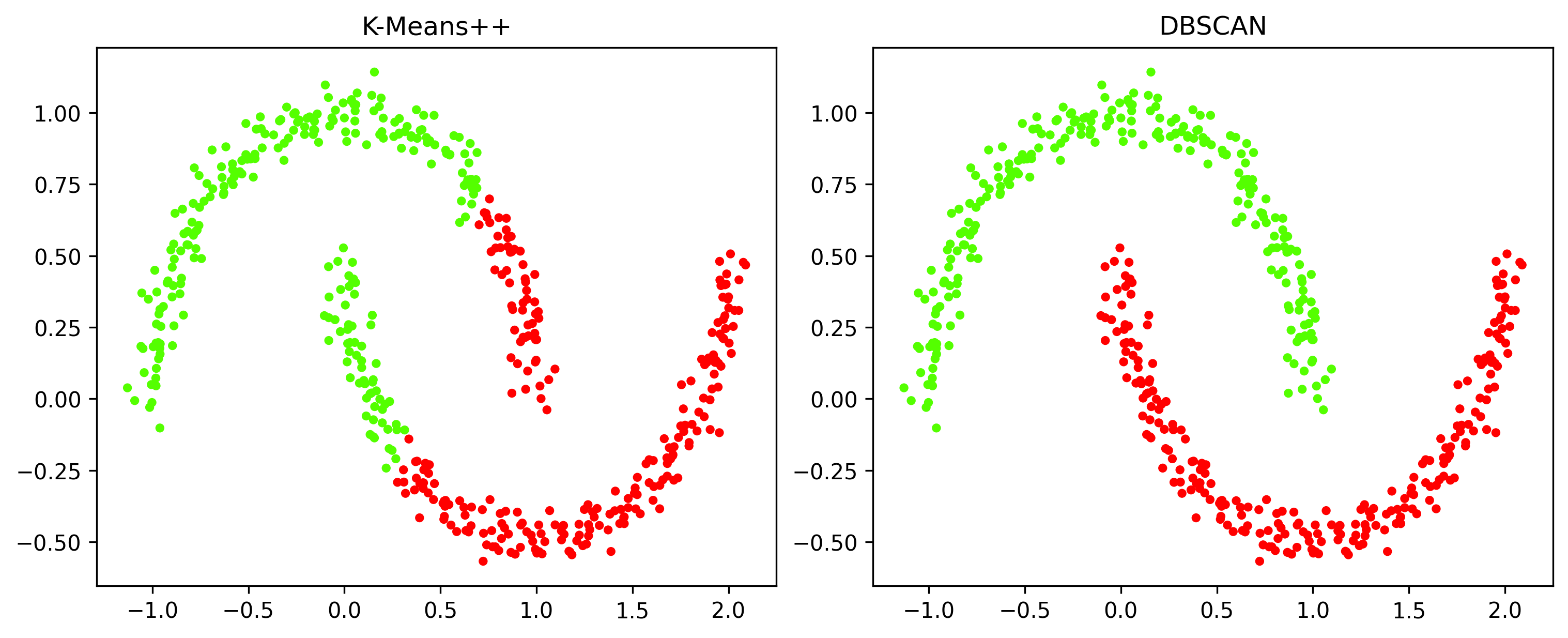
Spectral Clustering Algorithm
Spectral Clustering Algorithm (스펙트럼 군집화 알고리즘) 은 PCA를 이용한 군집화 알고리즘이다. PCA를 이용해 고차원의 데이터를 저차원으로 변환하고, 변환된 데이터를 기반으로 K-Means 등의 clustering 기법을 이용해 데이터를 군집화한다. scikit-learn의 SpectralClustering이 이 알고리즘을 구현하고 있다.
from sklearn.cluster import SpectralClustering
label_sca = SpectralClustering(n_clusters=2, affinity='nearest_neighbors', assign_labels='kmeans').fit_predict(coord1)
# affinity = 데이터 간의 유사도를 계산하는 방식
# assign_labels = pca 이후 군집화 방식
# 시각화로 확인해보기
plt.scatter(coord1[:,0], coord1[:,1], s=5, c=label_sca, cmap='jet')