베이지언 분류기의 문제점들 중 하나는 사전 확률 (prior probability) 과 가능도 (likelihood) 를 정확하게 계산하기 힘들다는 점이다. 그 이유는 우리가 예측하고자 하는 현실의 문제는 수많은 조건들이 얽혀 있어 굉장히 복잡하기 때문이다. 조건(차원)이 증가하면서 학습 데이터의 수가 차원의 수보다 적어지면 학습의 성능이 저하된다. 이를 차원의 저주 (The curse of dimensionality) 라고 한다.
나이브 베이즈 분류 (Naive Bayes Classification)
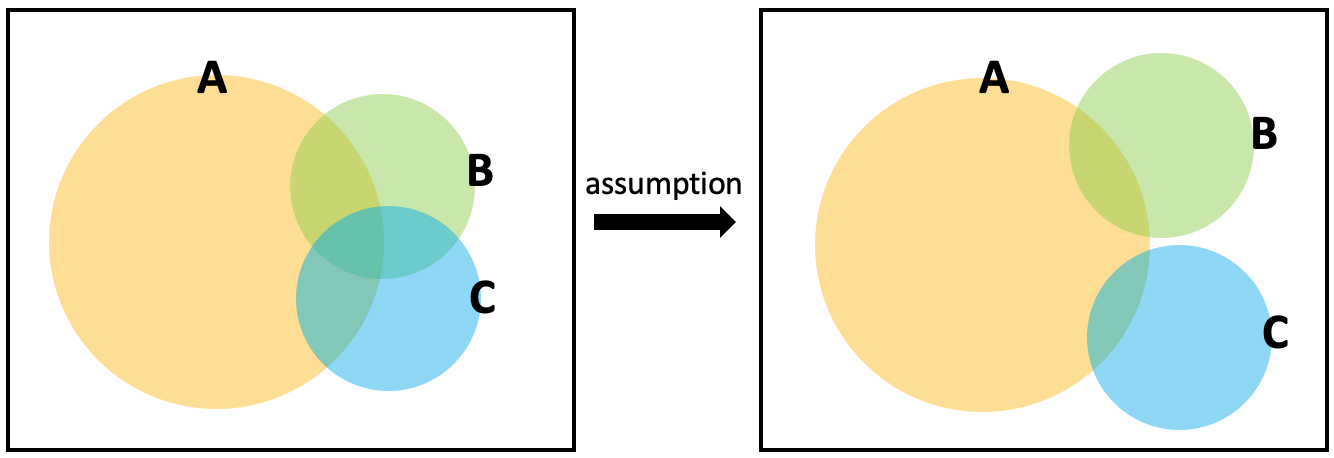
이를 해결하기 위한 방법 중의 하나가 나이브 베이즈 분류이다. 나이브 베이즈 분류란, 각 조건들 사이의 관계가 독립적이라고 가정하고 베이즈 정리를 적용한 확률 분류이다. 아래 도식을 보면, 현실의 문제는 왼쪽 그림들처럼 여러 조건들이 얽혀 있어 확률을 일일이 따져 계산하기가 복잡하다. 그러나 각 조건 (B, C)가 서로 독립적이라고 가정하면, 고려해야 할 경우의 수 (ex) , 등) 가 줄어들면서 계산이 간단해지게 된다. 이것이 나이브 베이즈 분류의 개념이다. 간단하게 가정을 한 만큼 현실과는 차이가 생길 수 있지만 근사적으로 현실을 예측할 수 있다는 점에서 유용한 알고리즘이라 할 수 있겠다.
Gaussian Naive Bayes Classifier
Gaussian Naive Bayes Classifier는 나이브 베이즈 분류와 기본적인 원리는 같지만, training set의 분포가 정규 분포 (Gaussian distribution) 를 따른다고 가정하는 것이다.
우리가 세상의 모든 데이터를 전부 빠짐없이 수집하지 않는 이상, training set은 어디까지나 표본이다. 표본이 모집단을 대표할 수 있도록 잘 선정되었다는 가정이 있다면 바람직하겠지만, 보통 우리는 표본을 다루고 그 모집단의 분포가 어떠한지는 잘 알지 못한다.
보통은 표본의 수가 많아질수록 정규 분포에 가까워지므로 (→ 중심 극한 정리(central limit theorem)), 정규 분포는 표본의 분포를 근사하는데 자주 사용된다. 이 원리를 이용해 training set의 분포가 정규 분포를 따른다고 가정하고 나이브 베이즈 분류를 하는 것이 Gaussian Naive Bayes Classifier이다.
References
https://en.wikipedia.org/wiki/Naive_Bayes_classifier
https://devkor.tistory.com/entry/Gaussian-Naive-Bayes
