Gaussian Perturbation

Score matching의 pitfalls(manfiold, low densitiy에 대한 부정확한 score estimation, 느린 mode change)는 모두 gaussian perturbation을 통해 해결 할 수 있다.

• Manifold
  nosie를 더한 형태의 manifold data는 gradient 정의가 가능해진다. 실제로 noisy data에 대한 score mathcing loss는 더 안정적으로 수렴한다.
  

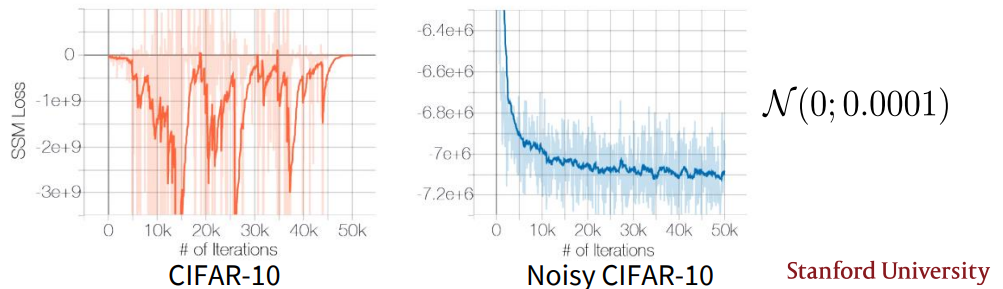
• Low density regions
  data dnesity가 perturbed 되었기 떄문에 low density에 대한 영역도 정확한 score estimation이 가능해 진다.
  

• Mode change
  low density에 대한 estimation이 정확해지면 자연스럽게 mode change도 좋아진다.

더 많은 nosie를 더 하면 당연하게 data quality가 낮아진다. 반면 score estimation은 정확해진다. 즉, data quality와 score estimation은 trade-off 관계라고 볼 수 있다.

Noise Conditional Score Networks

Annealed Lagevin Dynamics

Annealed Lagevin Dynamics는 sampling을 $\sigma_1,\sigma_2,\cdots,\sigma_L$을 순차적으로 이용하여 Langevin Dynamics를 수행하는 방법이다. $\sigma_1$이 가장 큰 noise level을 가지며 점차적으로 noise level을 낮춰가는 방식으로 수행된다. 이전 nosie level에서 Langevin Dynamics를 수행한 samples 를 initial sample로 활용하여 Langevin Dynamics를 수행한다.

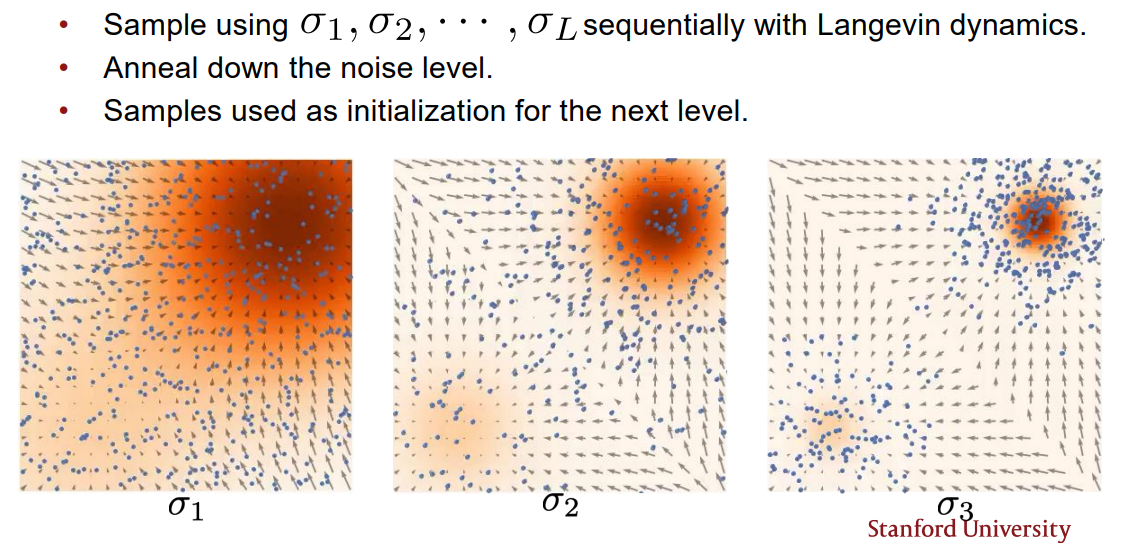
Nosie Conditional Score Networks(NCSN)

Annealed Langevin Dynamics를 사용하려면 모든 noise level에 대한 score estimation을 진행해야한다. 이는 각 noise level 마다 score estimation function(network) 가 필요할 수 있다는 것을 암시한다. 이러한 문제를 해결하기 위해 NCSN은 모든 noise level 에 대해 jointly optimizatino을 진행하는 방식을 제안한다.

Loss Function

NCSN은 Denosing score matching의 loss function을 이용하면 자연스럽다. 왜냐하면 Denosing score mathcing 역시 perturbed data를 가지고 estimation하는 방식이기 때문이다. NCSN은 기본적인 Denosing score mathcing 방식에, noise level 마다 weight term을 추가한 형태로 loss function을 구성한다.

Choosing Noise Scales

Max noise leve $\sigma_1$은 datapoints 사이의 maximum distance와 유사하게 설정하는 것이 좋다. 반면 minimum noise level $\sigma_L$ 은 origin data와 거의 차이가 없을 정도로 작게 설정하는 것이 좋다.

또한 인접한 noise scales는 충분히 overlab 될 수 있도록 간격을 설정하는 것이 좋다. 그 이유는 이전 level의 sampling output을 다음 level의 inital data로 사용할 것이기 때문이다. 일반적으로 다음과 같은 수식이 성립하도록 noise level을 설정한다.

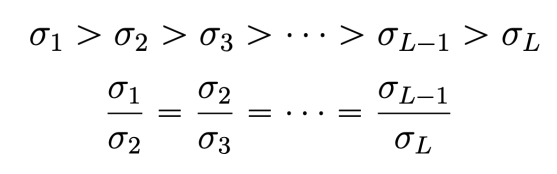
Choosing Weight of Scales

Scale에 대한 weight는 각 score matching loss의 balancing을 맞출 수 있도록 $\sigma_i^2$로 설정하는 것이 좋다.

Training NCSN

NCSN의 trainning 은 다음과 같이 진행된다.

Score-based Generative Modeling via SDEs

Infinite Noise Levels

NCSN은 유한한 수의 nosie level을 이용한다. 즉, 몇개의 noise level을 사용할지 정해줘야 한다. 그러나 clean data로 부터 $T$ noise level을 더한 data를 만들 때, 그 사이에는 무한한 수의 noise level들이 존재 할 수 있다.

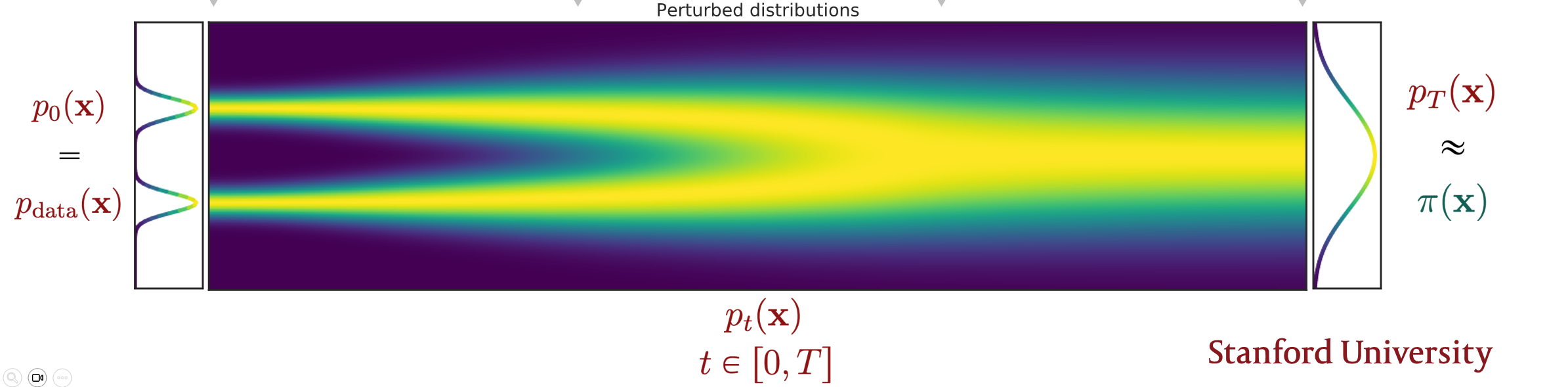
이러한 과정은 Stochastic Differential Equation(SDE) 를 통해 이루어질 수 있다. SDE의 식은 다음과 같다.

• $\mathrm{d}\mathbf{x}_t=f(\mathbf{x}_t,t)\mathrm{d}t+g(t)\mathrm{d}\mathbf{w}_t$

앞 쪽 $f$를 deterministic drift 라고 부르고 뒤 쪽 $\mathrm{d}\mathbf{w}_t$를 infinitesimal noise라고 부른다. 좀 더 단순하게 Toy SDE를 이용하면 generality를 잃지 않고 noise data를 얻을 수 있다.

• Toy SDE: $\mathrm{d}\mathbf{x}_t=\sigma(t)\mathrm{d}\mathbf{w}_t$

Reverse Stochastic Processes

Perturbed 된 data로 부터 origin data를 얻기 위해서는 reverse SDE를 수행하면 된다.

• Reverse SDE: $\mathrm{d}\mathbf{x}_t=-\sigma(t)\nabla_\mathbf{x}\log p_t(\mathbf{x_t})\mathrm{d}t+\sigma(t)\mathrm{d}\bar{\mathbf{w}_t}$

Reverse SDE의 앞쪽 term($\nabla_\mathbf{x}\log p_t(\mathbf{x_t})$) 이 score function과 동일한 것을 확인 할 수 있다.

Modeling

위 과정을 이용한 Score-based models의 modeling은 다음과 같다.

Euler-Maruyama 는 reverse SDE를 근사하는 방식이다.

Reference

cs236 Lecture 14