Converting the SDE to an ODE

SDE를 Ordinary differential equation(ODE)로 변경 가능하다. ODE 식은 다음과 같다.

• ODE: $\frac{\mathrm{d}\mathbf{x}_t}{\mathrm{d}t}=-\frac{1}{2}\sigma(t)^2\nabla_\mathbf{x}\log p_t(\mathbf{x_t)}$

위 식의 $\log p_t(\mathbf{x_t)}$ 은 score function으로 앞서 본 score based model인 $s_\theta(\mathbf{x},t)$로 approximation 한다. ODE로 변경하게 되면 더 이상 noise를 더하는 term이 존재하지 않게 된다. 따라서 ODE process의 결과는 deterministic 하다. 그리고 deterministic 하기 때문에, ODE와 invert ODE는 유일하게 존재하며, 이는 normalizing flow 모델과 동일하게 생각할 수 있다. 즉, SDE가 여러 VAE가 연속된 구조를 갖는다면 ODE는 normalizing flow 모델이 연속된 구조를 갖는다고 볼 수 있다.

또한 ODE는 다음과 같은 식을 통해 likelihood 계산을 진행할 수 있다.

• $\log p_\theta(\mathbf{x}_0)=\log \pi(\mathbf{x}_T)-\frac{1}{2}\int^T_0\sigma(t)^2\operatorname{trace}(\nabla_\mathbf{x}s_\theta(\mathbf{x},t))dt$

Latent Diffusion Model

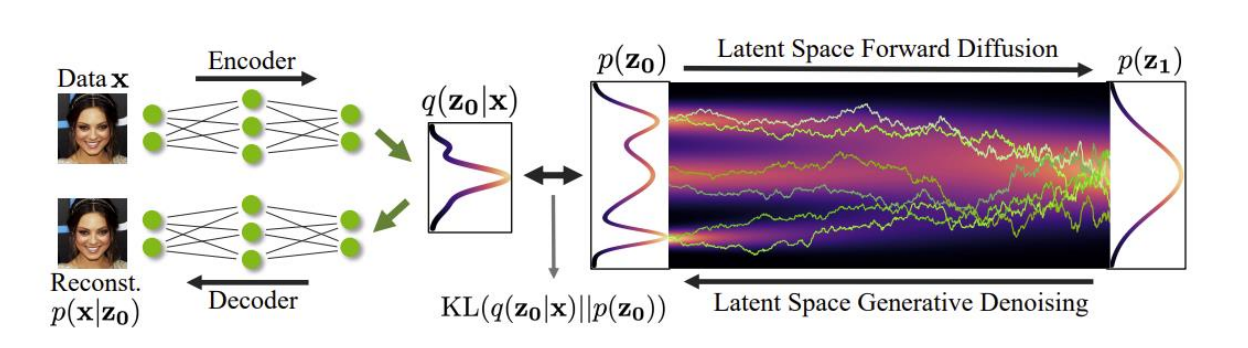
Latent diffusion model은 latent space에서 diffusion process를 진행하는 model이다. 일반적으로 VAE를 이용해 latent vector를 얻고 이를 diffusion process에 활용한다.

Control the Generation Process

Classifier Guidence

Generation 시, 특정 class 만을 나오도록 process를 control 하는 것은 다음과 같은 수식으로 생각할 수 있다.

• $\mathbf{y}$: Control signal (예를 들면 특정 강아지, 고양이 같은 특정 class)
• $p(\mathbf{x|y)}$: control signal을 condition으로 하는 distribution. 이 distribution에서 sampling.
• $p(\mathbf{y|x})$: forward model. (classifier)

bayes' rule을 활용하면 conditional distribution에 대한 새로운 학습 없이, conditional distribution을 얻을 수 있다.

• $p(\mathbf{x|y)}=\frac{p(\mathbf{x})p(\mathbf{y|x)}}{p(\mathbf{y})}$

$p(\mathbf{x})$ 에 대한 학습이 끝났고, pre-trained 된 classifier $p(\mathbf{y|x})$을 갖고 있다고 할 때, 위 식을 이용하면 새로운 condition distribution에 대한 학습 없이 conditional distribution을 얻을 수 있다. 하지만 $p(\mathbf{y})$를 계산하기 매우 어렵다는 단점이 있다. ($p(\mathbf{y|x)}$를 모든 $\mathbf{x}$에 대해 mariginalization 해야 함.)

위 식을 score fuction들로 변경하면 위의 단점을 해결할 수 있다.

• $\nabla_\mathbf{x}\log p(\mathbf{x|y})=\nabla_\mathbf{x}\log p(\mathbf{x})+\nabla_\mathbf{x}\log (\mathbf{y|x)}-\nabla_\mathbf{x}\log p(\mathbf{x)}=\nabla_\mathbf{x}\log p(\mathbf{x})+\nabla_\mathbf{x}\log p(\mathbf{y|x)}$

Classifier-Free Guidence

Pre-trained classifier를 활용하는 대신, conditional score model 과 unconditional score model을 학습하여 generation process를 control 할 수 있다. 이 상황에서 $p(\mathbf{y|x})$ 는 이제 unknown 이고, conditional model은 학습을 통해 얻는다.

이미 conditional model을 학습 했기 때문에 generation process에 condition을 반영하는 것은 가능하다. classifier-free guidence의 의미는 반영하고자 하는 condition을 더 강하게 반영할 수 있도록 조절 가능하다는 점이다. condition 반영에 대한 조절은 아래의 식을 통해 가능하다.

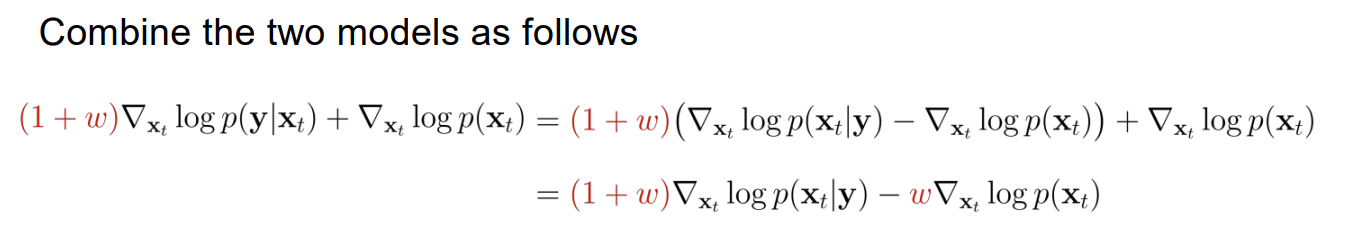
$\omega$를 classifier_guidence strength라고 부르며 이 값을 조절해 condition 반영에 대한 조절이 가능하다.

Reference

cs236 Lecture 17