[Computer Graphics] 4. Geometry Transformation

Lern-Backup·2021년 10월 15일
Computer Graphics
0

Computer Graphics

목록 보기
4/5

1. 3차원 물체의 표현

Object Modelling

Surface Representation : 물체 표면 표현

  • Polygon, Mesh
  • Rectangular mesh : 네 점이 한 평면 위에 있다는 것을 보장하지 못함
  • Triangular mesh : 삼각형은 네 점이 한 평균 위에 있다는 것을 보장할 수 있음, 높은 정밀도, 삼각형 분할을 위한 두 배의 처리시간

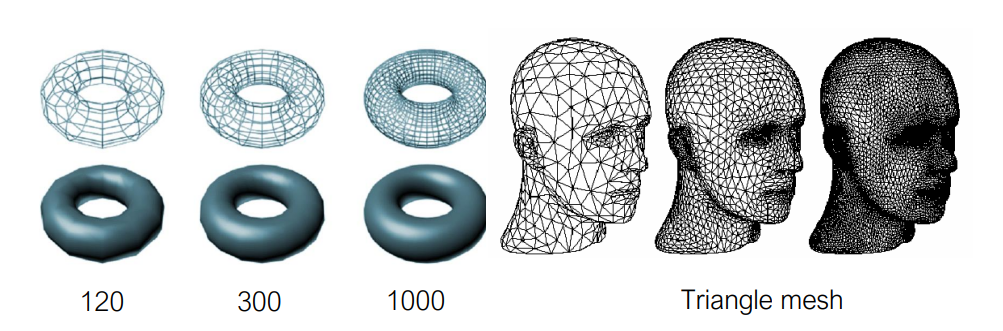
Rendering

  • 조명, 음영, 질감, 가시성등과 같은 물리적 효과를 계산하여 객체 모델에서 실제 장면을 그림
  • Wirwframe rendering : 빠름, 모델링 단계를 위함
  • Solid rendering : 느림, 디자인 리뷰를 위함

2. 벡터 공간

Vector Sapce

Scalar

  • 크기는 있지만 방향은 없음
  • 실수

Vector

  • 크기와 방향을 가지지만 origin(기원?)이 없음
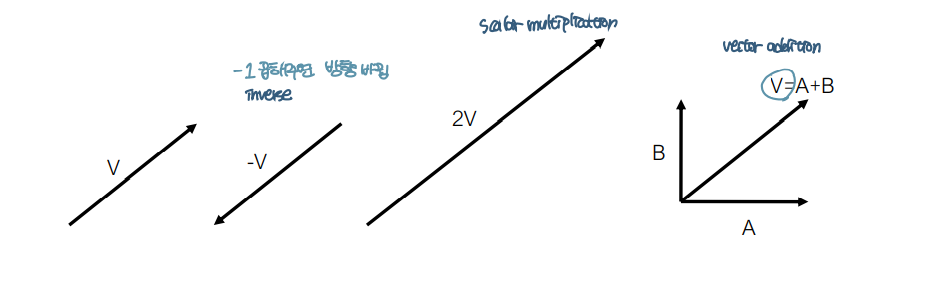
  • operations : 역, 스칼라 곱셈, 벡터 덧셈
  • 객체 정점 정의 및 그래픽 렌더링 계산에 사용

3. 어파인 공간

Affine Space

  • 동일한 크기 벡터는 시작점의 부재로 동일한 것으로 간주됨
  • 크기와 방향이 같다면 같은 벡터로 인식

Affine Space

  • 점의 개념에 의해 추가된 확장된 벡터 공간
  • 벡터의 시작점도 나타낼 수 있음

Affine operations

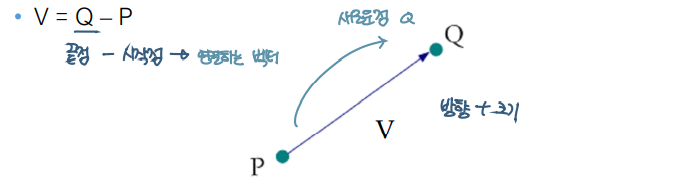
  • V = A + B : 벡터 사이의 덧셈
  • V' = 2V : 벡터와 스칼라 사이의 곱셈을 의미
  • Q = V + P : 벡터 및 점은 새 점을 정의

4. 좌표축과 좌표계

  • 벡터는 primary aexes(x, y, z)에 대해 basic vectors(v1, v2, v3)로 나타내짐

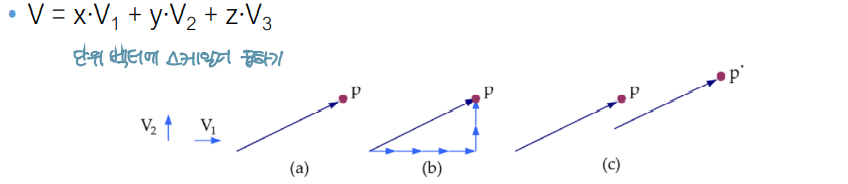
A Coordinate System (좌표 시스템)

  • origin과 basic vector로 이루어진 프레임
  • 있으면 임의의 점 정의 가능
    ➡ C = (r, v1, v2, v3)

점은 좌표계에 의해 표현

  • P = r + 4V1 + 3V2 + v3
  • r : 점

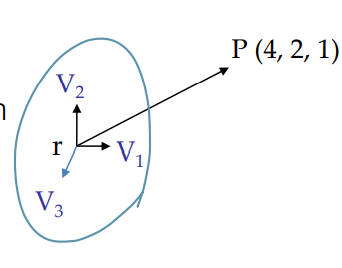
5. 동차 좌표

Homogeneous Coordinate System

  • 동차 좌표계 : 차원이 같음
  • 포인트 시작점 보존
  • 벡터는 시작점이 없음

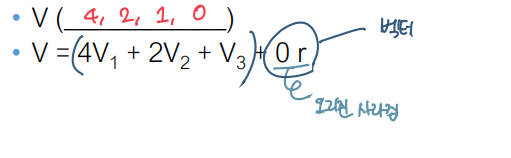
기하 변환

  • Transformation 이동
  • Rotation 회전
  • Scaling 크기
  • 객체를 변환하려면 객체 꼭짓점과 변환 matrix 사이의 곱셈에 의해 수행됨

1. 이동

2D Translation

  • P(x, y) : Vertex point matrix (정점)
  • P (Tx, Ty) : 이동 변환 matrix
  • P' (x', y') T(Tx, Ty) * P (x, y) ⬅ 이동 변환 matrix
  • x' = x + Tx
  • y' = y + Ty
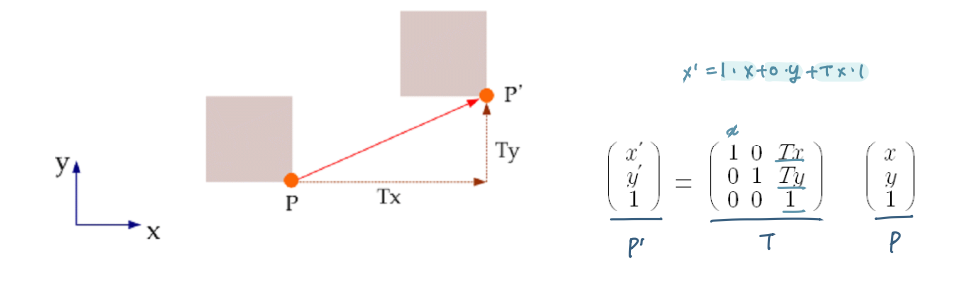
  • 새로운 좌표점을 구하는 것

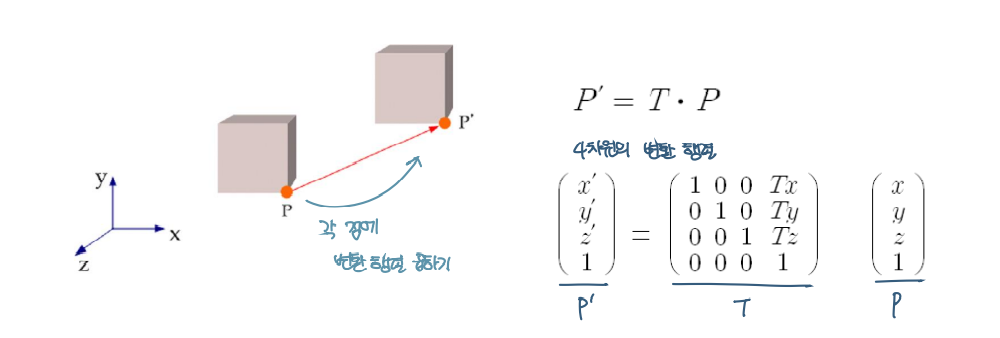
3D Translation

  • P (x, y, z) : A vertex point matrix (정점)
  • T (Tx, Ty, T2) : 이동 변환 matrix
  • P' (x', y', z') = T * P : T의 이동변환 후의 점
    x' = x + Tx, y' = y + Ty, z' = z + Tz

2. 회전

2D Rotation

  • 원점 회전만 존재
  • R : 원점 중심으로 회전
  • P' = R * P
  • Since x = rcosθ, and y = rsinθ

3D Rotation

  • x, y, z axis rotation
  • θ : 회전 각도
  • Right-handed system : OpenGL
  • Left-handed system : Unity, DirectX
  • Rz : Z-rotation (z는 앞뒤이므로 변화 X)
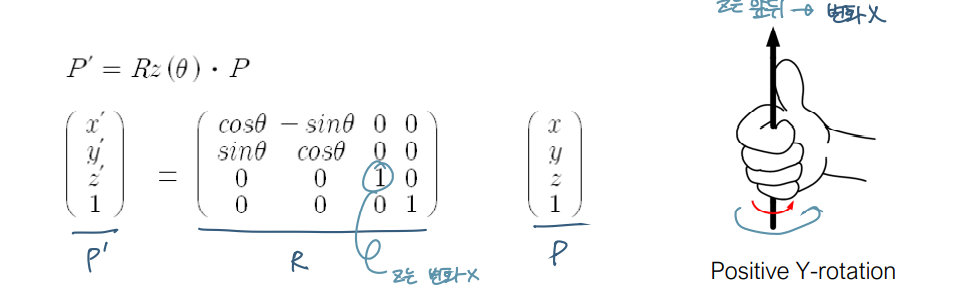
  • X-axis rotation : OpenGL
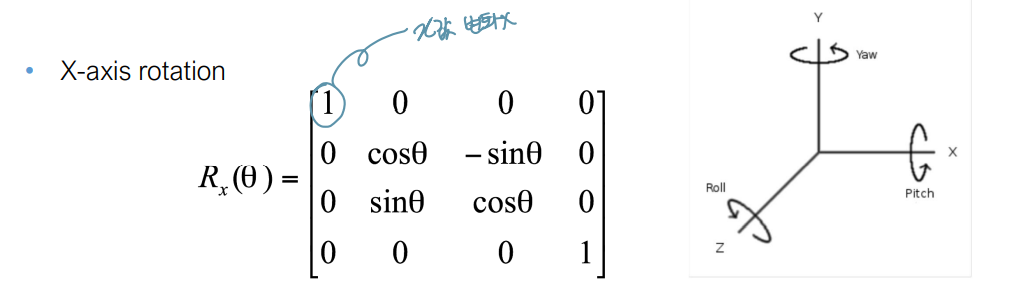
  • Y-axis rotation : Unity

3. 크기 조절

Scaling

  • Uniform vs Non-uniform scaling
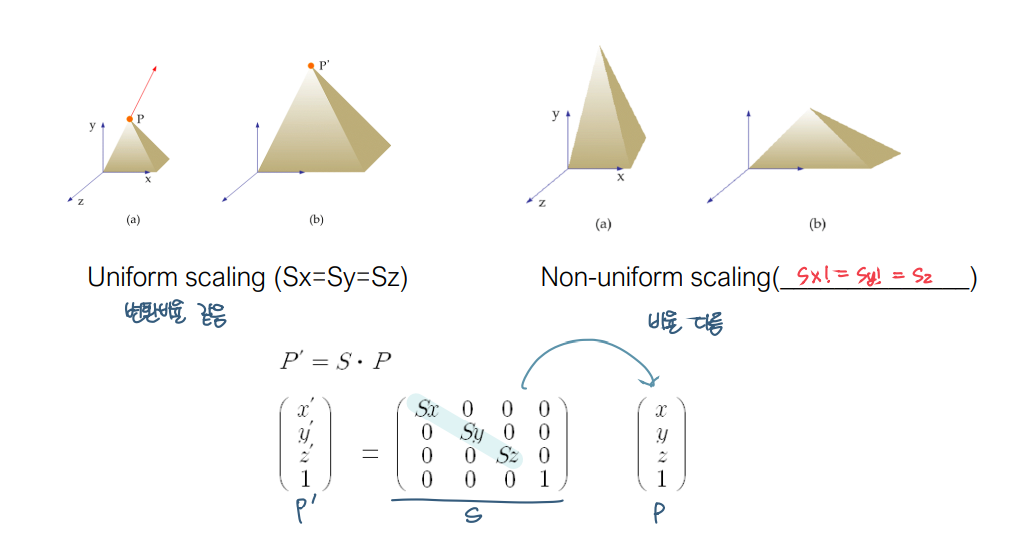
  • 변환 비율에 따라 나뉨

4. 복합 변환

Composite Transformation

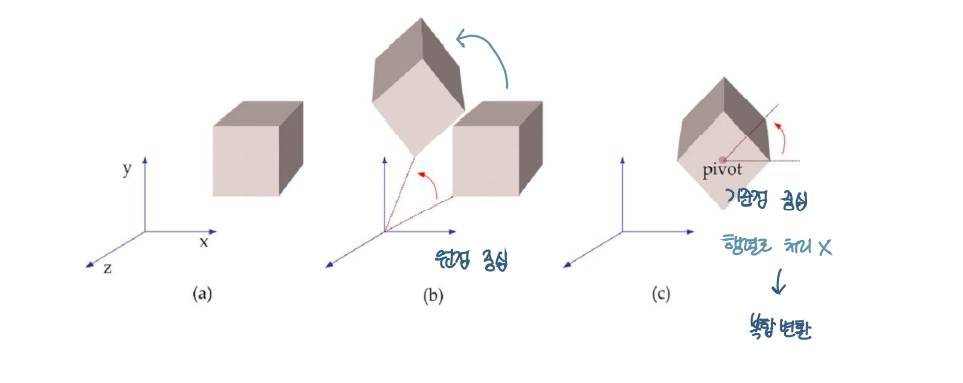
  • (a) Original position of a cube
  • (b) Origin-based rotation (원점 중심)
  • (c) Pivot point rotation (큐브의 중심)
  • 변환 순서는 T1 > Rotate > T2

Pivot Point Rotation

  • pivot 지점이 원점과 겹치도록 개체를 이동 T(-P)
  • 회전축에서 물체를 회전 : R
  • 회전된 물체를 다시 원래의 위치로 이동 : T(P)
  • 행렬은 변환의 역순으로 구함

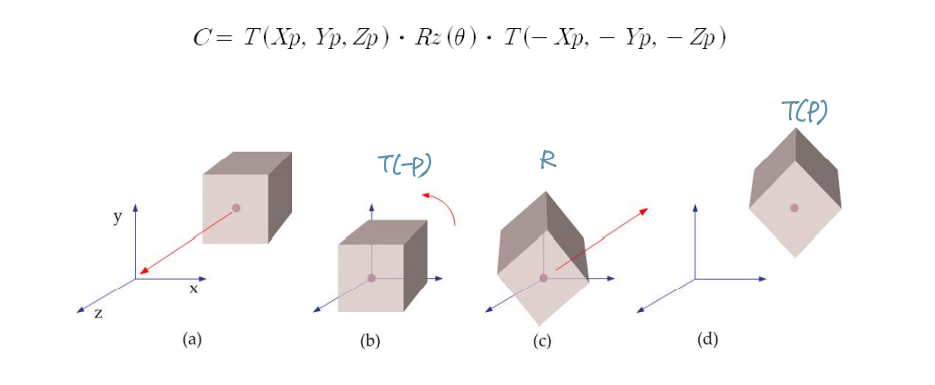
Compose Transformation

변환은 WCS에 기반

  • Translate(T1) > Rotate(R) > Translate(T2)

Matrix Multiplication in OpenGL (MCS에 기반)

  • P' = T2 R T1 * P ⬅ 교환좌표 성립 X
  • 복합 변환의 사전 컴퓨팅은 전체 처리 시간 절약 가능
  • P' = C P // C = T2 R * T1

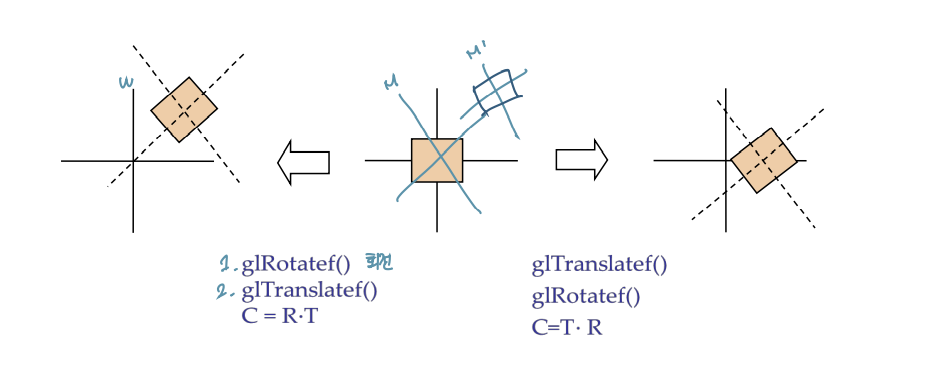
Transformation Order ⭐

matrix multiplication은 교환법칙 성립 X

  • Translate ➡ Rotate(R2 * Tx) // left
  • Rotate ➡ Translate(Tx * R2) // right

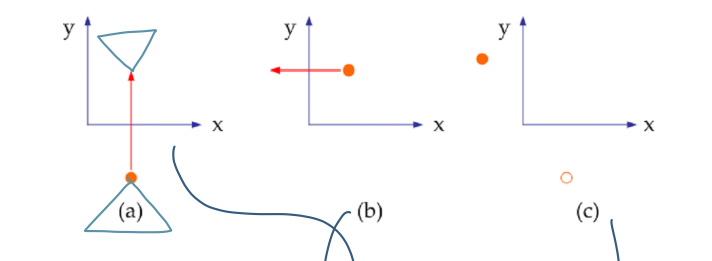
5. 반사

Reflection

  • (a) X-reflection (b) Y-reflection (c) Origin reflection
  • Origin-Reflection Matrix

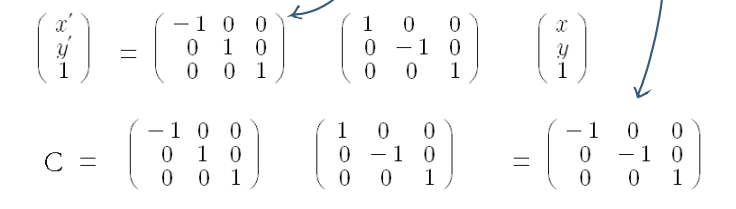
Composite Reflection

선 y = x에 대해 반사 (WCS 기반)

  • 원점에서 점을 45도 회전 (R)
  • 점의 y축 반사 (Y)
  • 원점에서 점을 -45도 회전 (-R)

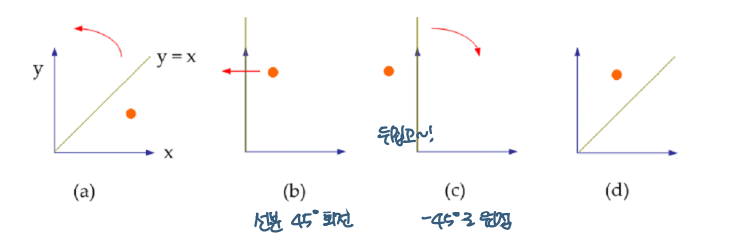
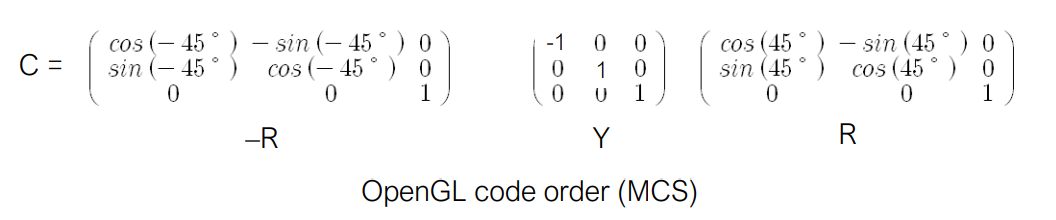
6. 구조 왜곡

Structure-Deforming Transformation

Non-deforming transformation 구조변환

  • 스케일링, 변환, 회전

Tapering : (a) > (b)

  • Along z-axis, an object is scaled

Bendeing : (a) > (C)

  • Along an axis, an object is bent (완전 형태 바뀜)

Twisting : (d) > (e) 뒤틀림

  • Along z-axis, a rotational angle increases

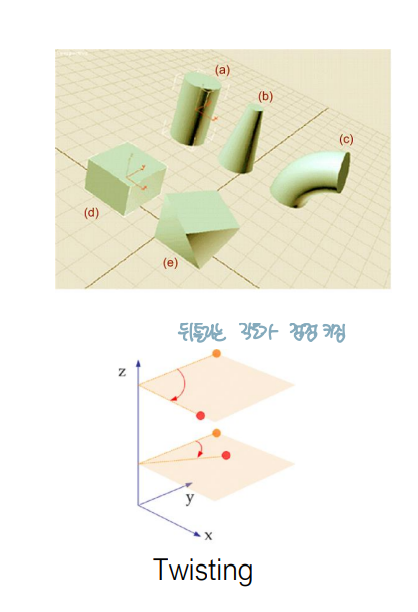
7. 변환의 분류

Transformation Classes

Rigid Body Transformation 감체

  • 물체형태 보존
  • ex) translation, rotation

Similarity Transformation 유사변환

  • 폴리곤 사이의 각도와 vertex 유지
  • ex) rigid-body transformation + uniform scaling, reflection

Affine Transformation Object 형태 유지

  • 물체의 선, 다각형, 곡면, 평행선 등의 객체 항상 유지
  • ex) Similarity transformation + non-uniform scaling, shearing

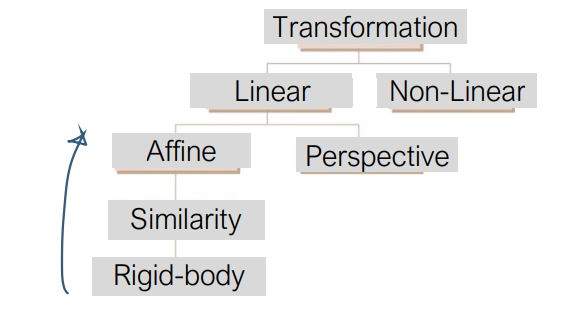
Perspective Transformation

  • 평행선이 만남
  • 직선 유지

Linear Transformation 선형 변환

  • 선형 함수 x, y, z as x' = ax + by + cz로 구성
  • 직선 유지
  • ex) Affine + perspective trans

Non-linear transformation 비선형 변환

  • x' = ayx + by2 + cz/x
  • 상수 간의 곱셈, 1차 함수 x
  • ex) structure-deforming trans > no guarantee of keeping straight lines

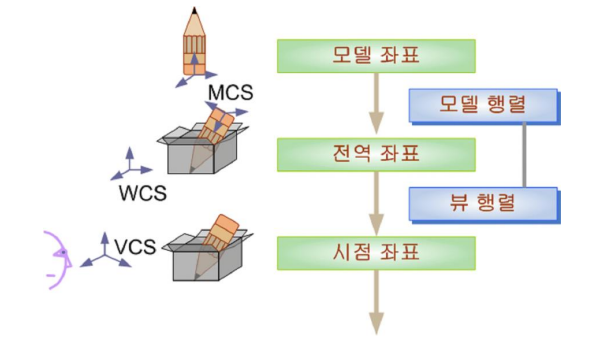
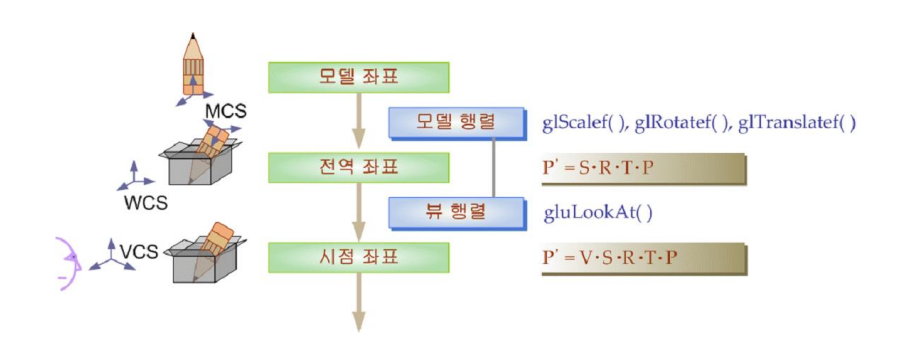
1. 모델 좌표계와 전역 좌표계

Modeling Coordinate System

MCS

  • 모델링 단계에서 사용되는 객체별 좌표
  • 임의의 좌표 원점 및 단위 보유

WCS, MCS and VCS

World Coordinate System

  • 여러 MCS를 하나로 통합
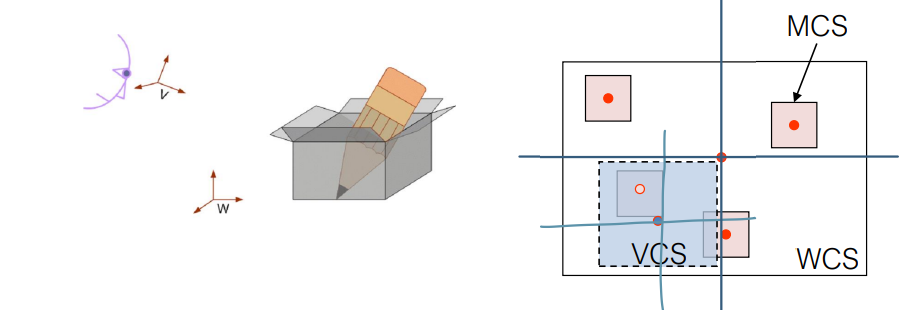
  • 최종 스크린 ➡ VCS

View Coordinate System

  • 카메라가 정의한 좌표계
  • viewing space가 viewport로 이전

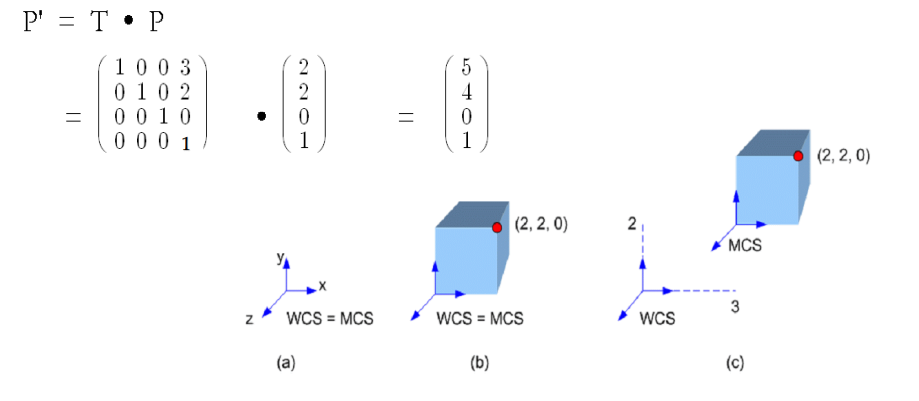
Matrix Multiplication

  • 물체의 꼭짓점 좌표는 transformation으로부터 분류
  • 물체가 변환될 때, vertex matrix에 변환 행렬을 곱해 WCS 위치를 얻음
  • P'(WCS) = Translate * P(MCS)

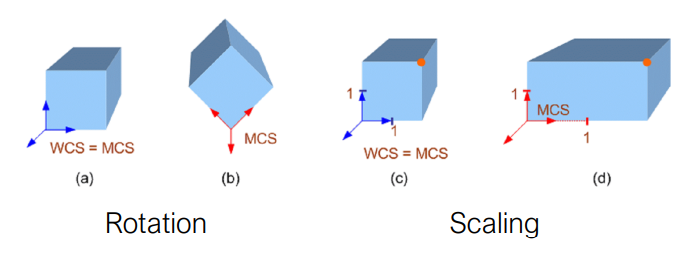
Rotation

  • MCS가 물체와 회전

Scaling

  • 스케일링으로 MCS와 WCS의 비율 변환
  • Scaling by 2 on x-axis > WCS : MCS = 2 : 1
  • P'(WCS) (4, 2, 0) = S(2, 1, 1) x P(MCS) (2, 2, 0)

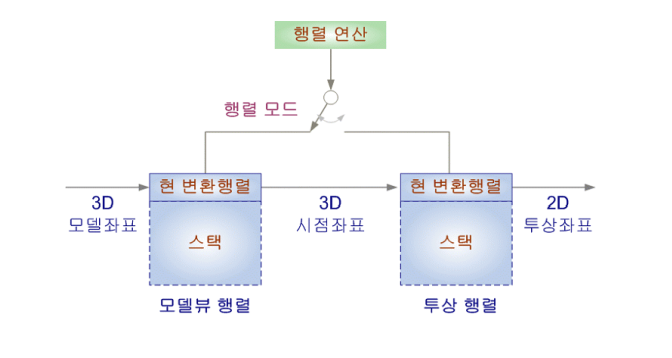
2. 지엘 파이프라인

ModelView Matrix

Modeling Transformation

  • Translation, rotation, scaling of an object

Viewing Transformation

  • 좌표계 보기 정의 방법
  • 카메라의 위치 및 방향별

ModelView 시스템은 하나의 system matrix에서 관리

  • 역변환 관계 (카메라 move - 모델 move)

3. 모델 변환

Matrix Stack

  • 변형이 발생하면 변환 매트릭스 push

glMatrixMode (GLenum mode)

  • GL_MODELVIEW
  • GL_PROJECTION
  • GL_TEXTURE

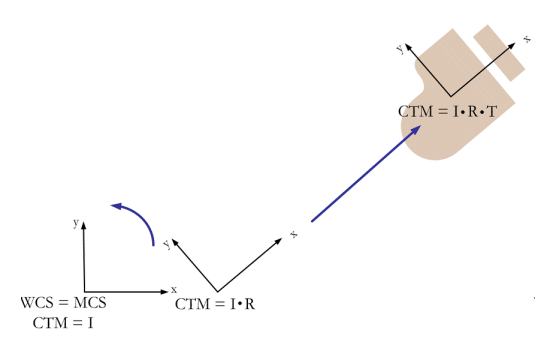
Object-based MCS

OpenGL

  • glMatrixMode(GL_MODELVIEW);
  • glLoadIdentity();
  • glRotatef(45, 0.0, 0.0, 1.0);
  • glTranslatef(10.0, 0.0, 0.0);
  • glVertex3f(x, y, z);

OpenGL Code-order

  • object와 함께 MCS 회전
  • Translate MCS on the lastest MCS
  • 최종 MCS 원점에 object가 그려져 있음

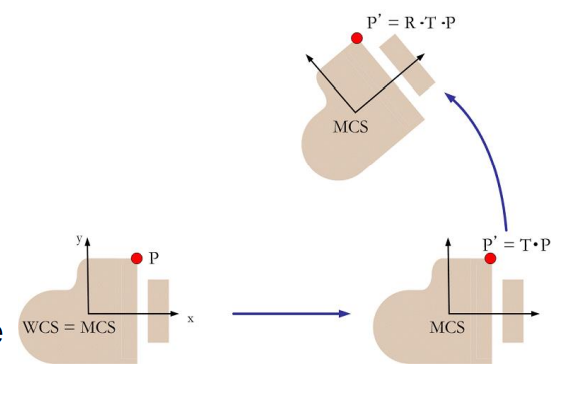
Origin-based WCS

OpenGL

  • glMatrixMode(GL_MODELVIEW);
  • glLoadIdentity();
  • glRotatef(45, 0.0, 0.0, 1.0);
  • glTranslatef(10.0, 0.0, 0.0);
  • glVertex3f(x, y, z);

Reverse order OpenGL code

  • WCS 원점에서 MCS 번역
  • WCS 원점에서 WCS 회전
  • 지난 MCS의 origin에 object 그리기

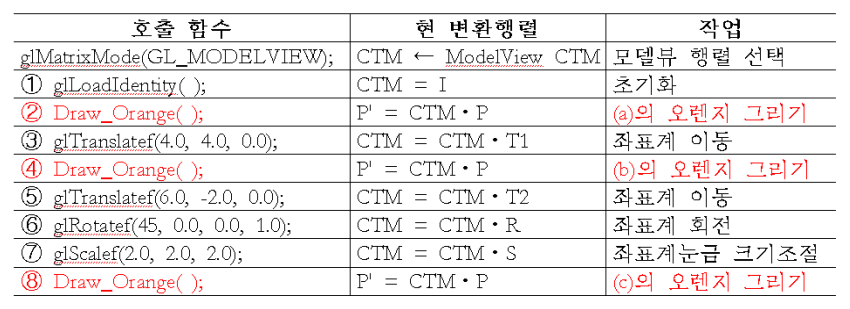
CTM

Current Transformation Matrix

  • 변환이 발생할때 그것은, system matrix stack의 최상위 요소인 CTM에 누적
  • object vertex matrix는 CTM을 곱한 후 그림

4. 복합 변환에 의한 모델링

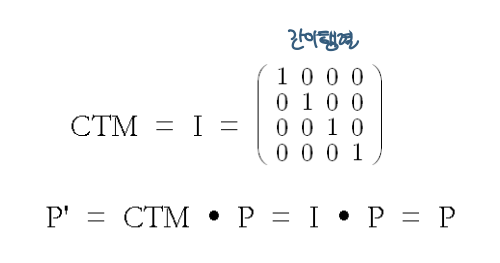
CTM Initialization

  • glLoadIdentity()

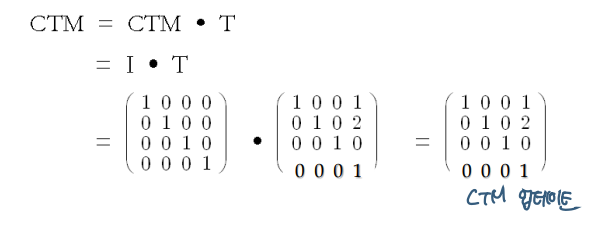
CTM accumulation

  • 오른쪽부터 CTM의 변환이 쌓임
  • CTM = CTM * M
  • ex) glTranslatef(1, 2, 0)

CTM

glMatrixMode(GL_MODELVIEW); 
glLoadIdentity(); // CTM initialized
glScalef(sx, sy, sz);
glRotatef(theta, vx, vy, vz);
glBegin(GL_POINTS); 
glVertex3f(x, y, z);
glEnd();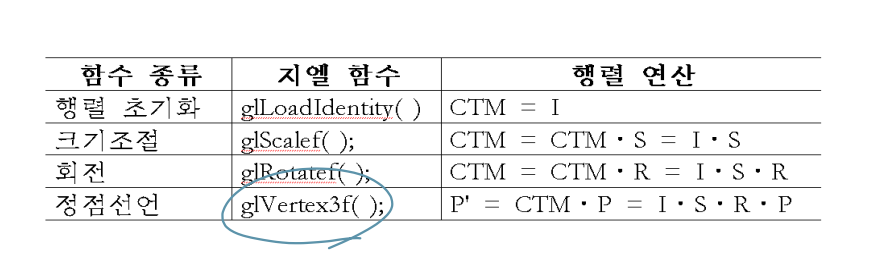

5. 행렬 스택 활용

Matrix Stack


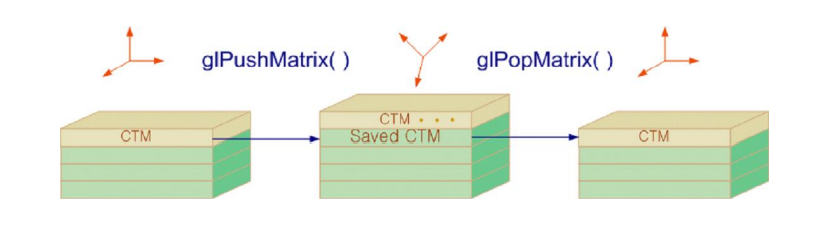
matrix stack에서 연속 변환 행렬 관리

  • matrix stack의 top은 CTM 의미
  • glPushMatrix() : 현재 CTM이 존재할 경우 CTM 복사해 push
  • glPopMatrix() : top CTM pop ➡ 이전 CTM 위치로 돌아감

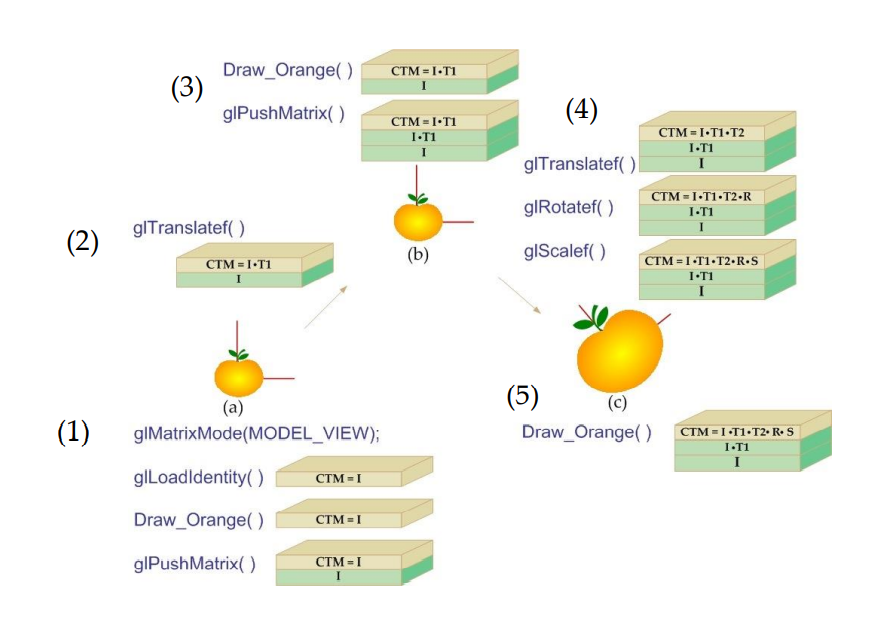
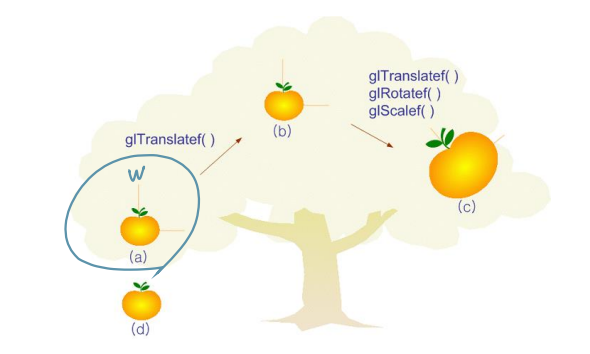
6. 계층 구조 모델링

Hierarchical Modelling

  • 계층적 모델링

Solar System

  • Scene tree 태양계



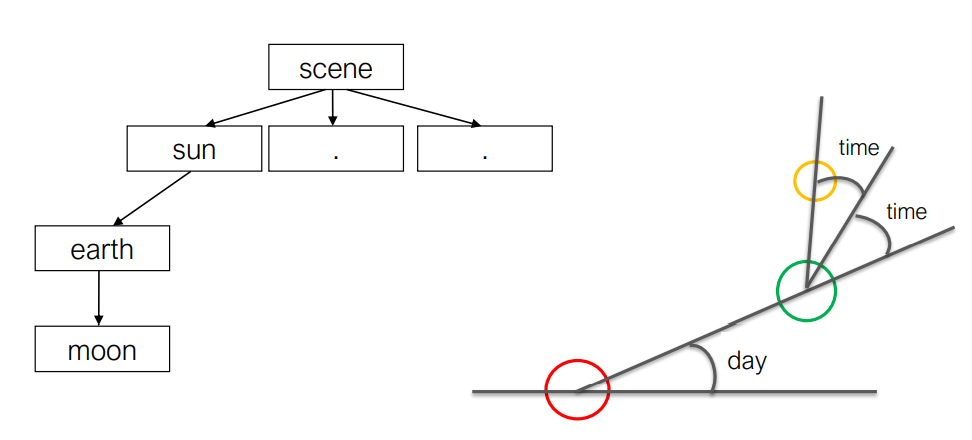
1. 시점 좌표계 설정

Viewing Transformation

Viewing Coordinate System VCS

  • 뷰 볼륨 안에 있는 object만 출력
  • 카메라 위치 및 방향에 의해 정의됨
  • 보기는 모델링 변환과 반대
  • model matrix + view matrix ➡ modelview matrix

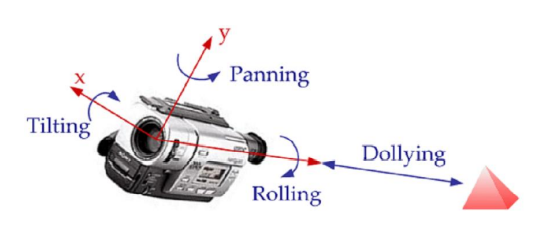
Camera Rotation

  • Tilting : X-rotation
  • Panning : Y-rotation
  • Rolling : Z-rotation
  • Dolling : Camera zoom-in/out

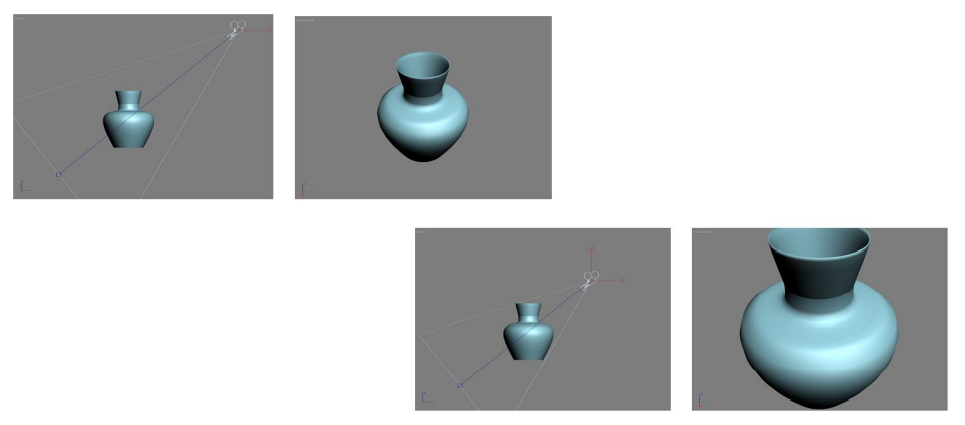
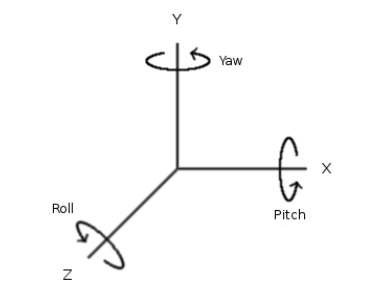
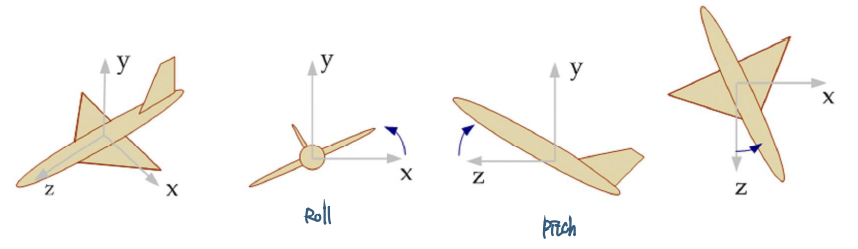
Flight Angels

  • 평면의 방향은 세 각도로 정의됨
  • Roll : Z-rotation angle (second)
  • Pitch : X-rotation angle (third)
  • Yaw : Y-rotation angle (last)

2. 지엘의 시점 좌표계

GL VCS

  • glulookAt

Viewing and Modelling Transformation

glMatrixMode(GL_MODELVIEW); 
glLoadIdentity( ); // I
gluLookAt(0.0, 10.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, .0); // V
glTranslatef (5.0, 5.0, 0.0); // T1
glTranslatef (4.0, 2.0, 0.0); // T2
glRotatef (45, 0.0, 0.0, 1.0); // R
glutWireCube(1.0); // PMCS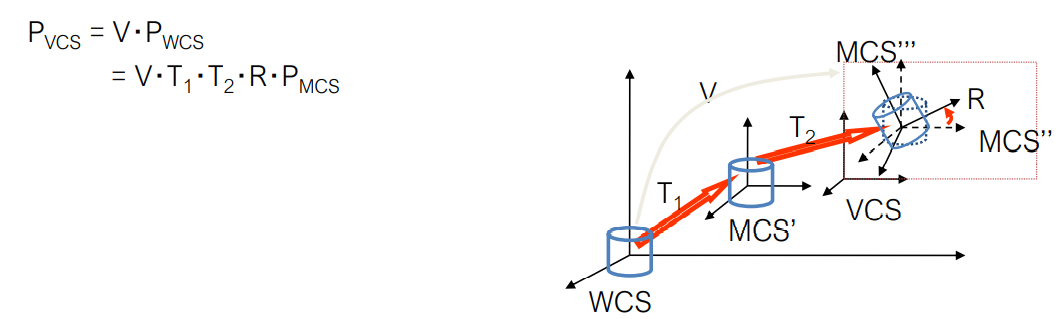

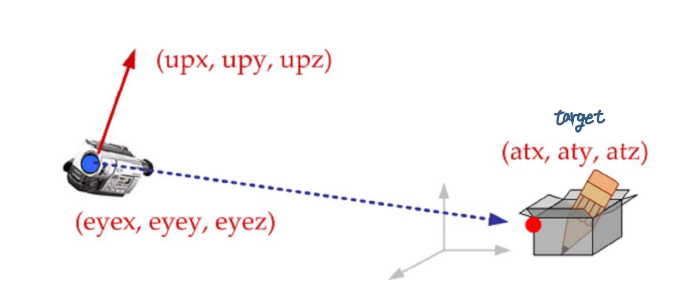
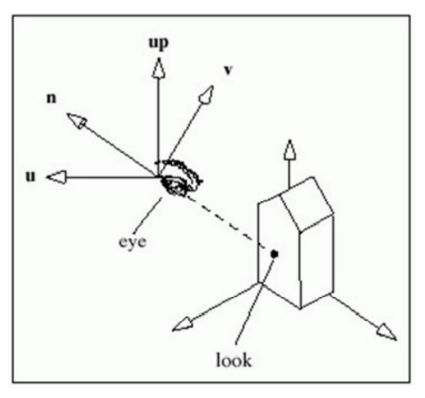
Camera Coordinate System

  • gluLookAt(eyex, eyey, eyez, atx, aty, atz, upx, upy, upz);
  • Axes : u, v, n
  • n = eye - at
  • u = up x n
  • v = n x u
  • origin : eye (looking in the direction -n)

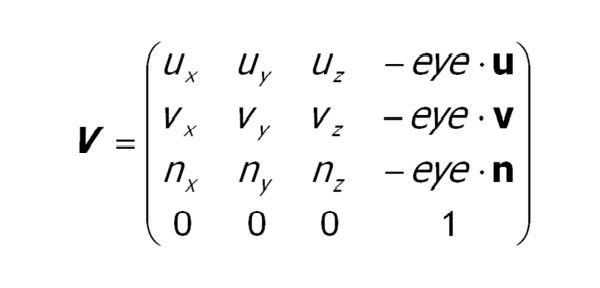
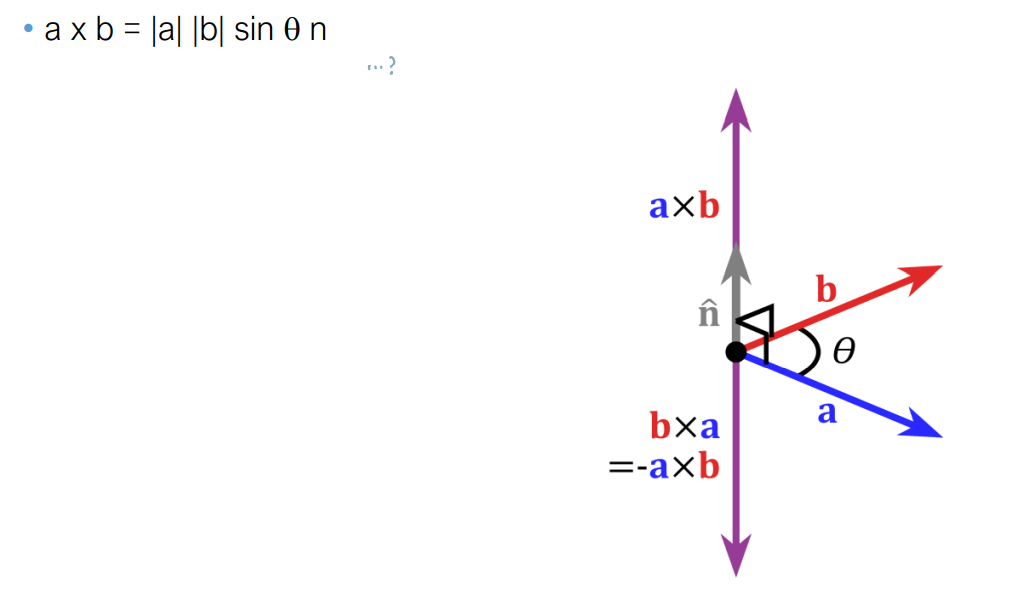
Cross Product

profile
Lern-Backup
공부 백업용
이전 포스트

[Computer Graphics] 3. Graphic Library

다음 포스트

[Computer Graphics] 5. Projection

0개의 댓글