[딥러닝]지도학습

권경민·2023년 7월 13일

딥러닝

목록 보기

3/8

3장 머신러닝 핵심 알고리즘

1. 지도학습

지도학습은 분류와 회귀로 나뉜다.

분류 : 데이터를 정해진 범주에 따라 분류
회귀 : 데이터의 특성을 기준으로 연속된 값을 그래프로 표현해 패턴이나 그래프를 예측

1.1 K-최근접 이웃

K-최근접 이웃이란?
새로운 입력을 받았을 때 기존 클러스터에서 모든 데이터와 인스턴스 기반 거리를 측정한 다음, 가장 많은 속성을 가진 클러스터에 할당하는 분류 알고리즘이다.

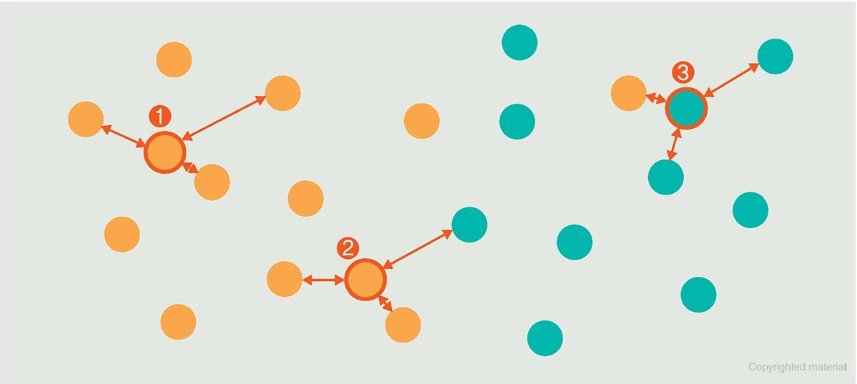새로운 입력 1, 2, 3(빨간선 원)에 대한 학습 절차
1️⃣ 주변 범주 세 개가 주황색이므로 주황으로 분류
2️⃣ 주변 범주 두 개가 주황색, 한 개가 녹색이므로 주황으로 분류
3️⃣ 주변 범주 두 개가 녹색, 한 개가 주황색이므로 녹색으로 분류

붓꽃 데이터로 K-최근접 이웃 코드 실습

# 데이터 준비
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import metrics

# 데이터셋에 colums이름  할당
names = ['sepal-length','sepal-width','petal-length','petal-width','Class'

# 데이터를 판다스 df에 저장
dataset = pd.read_csv('iris.data', names=names)

# 데이터 전처리 및 분리
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:,4].values

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 스케일링
from sklearn.preprocessing import StandardScaler
s = StandardScaler()
s.fit(X_train)
X_train = s.transform(X_train)
X_test = s.transform(X_test)

# 모델 생성 및 훈련
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=50) # K값을 50으로 정함
knn.fit(X_train, y_train)

# 모델 정확도
from sklearn.metrics import accuracy_score
y_pred = knn.predict(X_test)
print('모델 정확도: {}'.format(accuracy_score(y_test, y_pred)))

출력결과 : 모델 정확도: 0.9333333333333333

모델 생성 및 훈련 부분에서 K값을 50으로 정했다.
for문을 사용하여 K값을 1부터 10까지 순환하면서 최적의 K값과 정확도를 찾아보자.

# 최적의 K 찾기
k = 10
acc_array = np.zeros(k)
for k in np.arange(1, k+1, 1):
    classifier = KNeighborsClassifier(n_neighbors=k).fit(X_train, y_train)
    y_pred = classifier.predict(X_test)
    acc = metrics.accuracy_score(y_test, y_pred)
    acc_array[k-1] = acc
    
max_acc = np.amax(acc_array)
acc_list = list(acc_array)
k = acc_list.index(max_acc)
print('정확도', max_acc,'으로 최적의 k는 ',k+1,'이다.')

출력결과 : 정확도 1.0 으로 최적의 k는  1 이다.

1.2 서포트 벡터 머신

서포트 벡터 머신이란?
분류를 위한 기준선을 정의하는 모델7

즉, 분류되지 않은 새로운 데이터가 나타나면 결정 경계(기준선)을 기준으로 경계의 어느 쪽에 속하는지 분류하는 모델

💡 결정 경계란?
결정 경계는 데이터를 분류하기 위한 기준선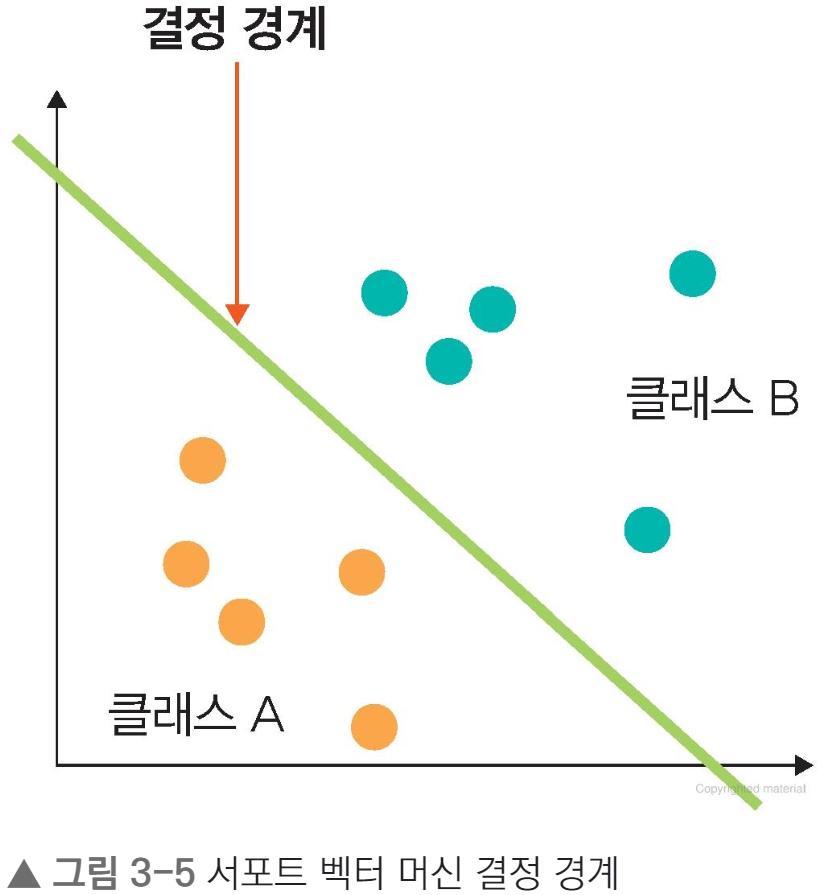

위와 같이 주황색, 녹색 공을 색상별로 분류하기 위한 기준선

⬆️ (b)가 가장 성능이 좋음.
-> 결정 경계는 데이터가 분류된 클래스에서 최대한 멀리 떨어져 있을 때 성능이 가장 좋음

💡 용어 정리

마진 (margin)이란?
결정 경계와 서포트 벡터 사이의 거리
- 소프트마진 : 이상치 허용
- 하드마진 : 이상치 불허용

서포트 벡터란?
결정 경계와 가까이 있는 데이터

▶️ 최적의 결정 경계는 마진을 최대화

서포트 벡터 머신 붓꽃 예제

from sklearn import svm, metrics, datasets, model_selection
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'   # 📍 주석 설명

📍 주석 설명
TF_CPP_MIN_LOG_LEVEL라는 환경 변수를 사용하여 로깅을 제어함.
(기본값은 0으로 모든 로그가 표시, INFO 로그를 필터링하려면 1, WARNING 로그를 필터링하려면 2, ERROR로그를 추가로 필터링하려면 3으로 설정)

iris = datasets.load_iris() # 사이킷런에서 제공하는 iris 데이터 호출
X_train, X_test, y_train, y_test = model_selection.train_test_split(iris.data, iris.target<, test_size = 0.6, random_state=42)

# SVM 모델 생성 및 훈련 후 예측 수행
svm = svm.SVC(kernel='linear', C=1.0, gamma=0.5) # 📍주석 설명1
svm.fit(X_train, y_train) # 훈련 데이터를 사용해 SVM 분류기 훈련
predictions = svm.predict(X_test) # 훈련 모델을 사용해 테스트 데이터로 예측
score = metrics.accuracy_score(y_test, predictions)
print('정확도: {0:f}'.format(score))

출력결과 : 정확도: 0.988889

📍 주석설명
SVM은 선형분류와 비선형분류를 지원함.
비선형에 대한 커널은 선형으로 분류될 수 없는 데이터때문에 발생.

비선형 문제를 해결하는 가장 근본적 방법은 저차원 데이터를 고차원으로 보내는 것

그러나 이는 많은 수학적 계산이 필요하고 성능에 문제를 줄 수 있음.
▶️ 이 문제를 해결하고자 도입한 것이 커널 트릭

💡 커널(kernel)

선형 모델을 위한 커널

선형 커널
선형으로 분류 가능한 데이터에 적용
$K(a,b) = a^T•b\\(a,b:입력벡터)$

비선형 모델을 위한 커널

다항식 커널
실제로는 특성을 추가 안하지만, 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있는 방법
= 엄청난 수의 특성 조합이 생기는 것과 같은 효과를 얻어 고차원으로의 데이터 매핑 가능 $K(a,b) = (ɣa^T•b)^d\\ (a,b:입력벡터\\ɣ:감마\\d:차원, 이때 ɣ,d는 하이퍼파라미터)$

가우시안 RBF커널
입력 벡터를 차원이 무한한 고차원으로 매핑하는 것으로, 모든 차수의 모든 다항식을 고려함.
다항식 커널은 차수에 한계 존재, 가우시간은 차수에 제한 없이 무한 확장 가능. $K(a,b) = exp(-ɣ||a-b||^2)\\(이때 ɣ는 하이퍼파라미터)$

1.3 결정 트리

결정트리란?
- 데이터를 분류하거나 결괏값을 예측하는 분석 방법
- 결과 모델이 트리구조기 때문에 결정트리라고 부름.

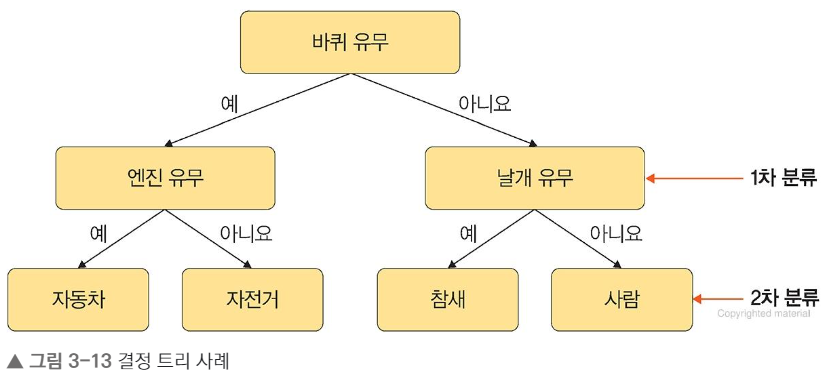
결정 트리는 데이터를 1차로 분류한 후 각 영역의 순도는 증가하고 불순도와 불확실성은 감소하는 방향으로 학습 진행함.

1.4 회귀

회귀란?
변수가 두 개 주어졌을 때 한 변수에서 다른 변수를 예측하거나 두 변수간의 관계를 규명할 때 사용

이 때 사용되는 변수 유형
1. 독립변수(예측 변수) : 영향을 줄 것으로 예상되는 변수
1. 종속변수(기준 변수) : 영향을 받을 것으로 예상되는 변수

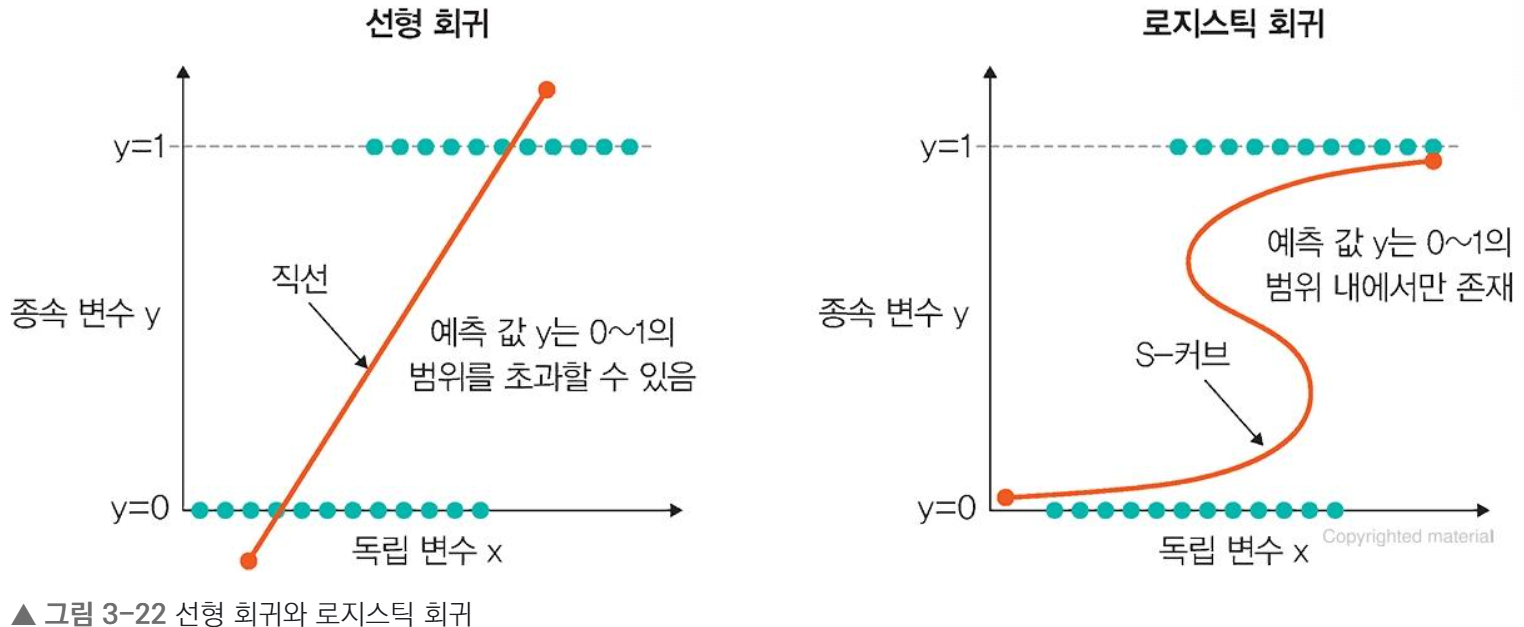
1.4.1 로지스틱 회귀

분석하고자 하는 대상들이 두 집단 이상의 집단으로 나눠진 경우, 개별 관측치들이 어느 집단으로
분류될 지 분석하고 예측하는 모델을 개발하는 데 사용되는 통계 기법

💡 최소제곱법과 최대우도법
최소제곱법(mean squared)과 최대우도법(maximum likelihood)은 랜덤 표본에서 모집단 모수를 추정하는데 사용된다.

최소제곱법(=평균제곱오차) : 실제값에서 예측값을 뺀 후 제곱해서 구함

최대우도법

우도(likelihood) : 나타난 결과에 따라 여러 가능한 가설을 평가할 수 있는 척도
∴ 최대우도 = 나타난 결과에 해당하는 가설마다 계산된 우도값 중 가장 큰 값
▶️ 일어날 가능성이 가장 큰 것

로지스틱 회귀분석 진행절차
1. 각 집단에 속하는 확률의 추정치 예측
└→ 이진 분류의 경우 집단 1에 속하는 확률 P(Y=1)로 구함

2. 분류 기준값을 설정한 후 특정 범주로 분류
ex) P(Y=1) ≥ 0.5 - 집단 1로 분류
. ㅤP(Y=1) < 0.5 - 집단 0으로 분류