고차원-> 저차원으로 바꾸는 이유는?
: 고차원에서 일어나는 차원의 저주 문제를 피하기 위함
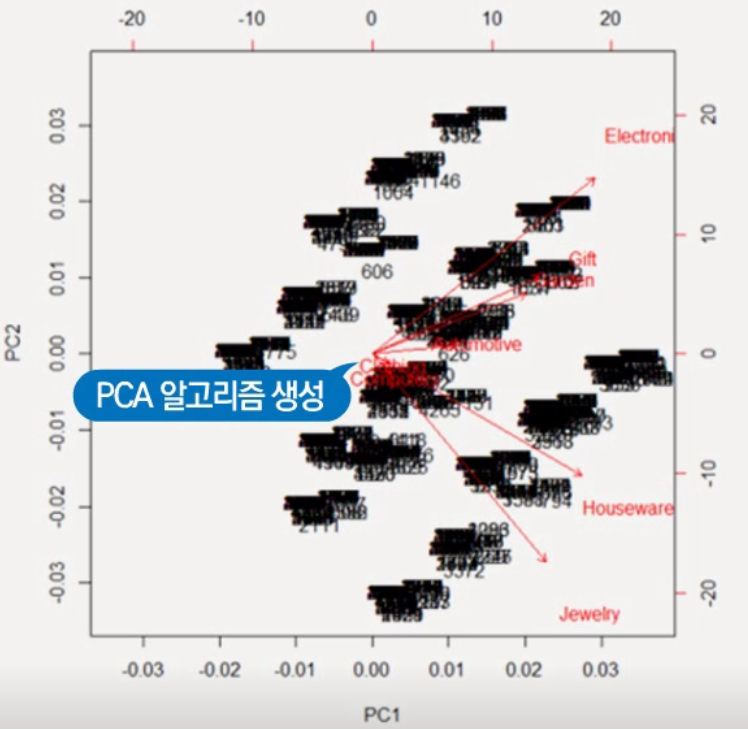
PCA(주성분 분석)
: 기존 원본 데이터의 최대한 정보를 살리면서 차원이 축소된 새로운 좌표 체계를 만들어 표현
<특징>
1. 새로운 축은 독립이며 직각임
2. 원본 데이터의 차원이 p라면 새롭게 만들어진 데이터의 차원은 k(<p)
3. 원본 데이터 X는 U와 V의 곱으로 분리됨
4. U는 데이터를 새로운 차원 k로 설명함
5. V는 원본 차원과 축소 차원의 관계를 설명함
6. 정보를 많이 잃어버리지 않고 차원을 축소시킴
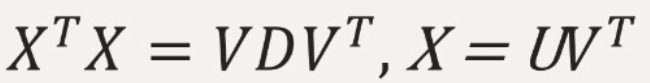
원본데이터 = X
스코어 행렬 = U
부하 행렬 = V
대각 행렬 = D

★P개의 차원을 K개의 차원으로 축소하였다. 정보손실을 최소화하는 K를 골라야 한다. 정확한 K를 골라주는 여러 가지 방법론이 있다.
DBSCAN
: 밀도기반으로 노이즈까지 잡아내는 탁월한 성능을 가진 군집분석
데이터 압축 → 거리함수 선정 → 군집 분석
이웃벡터
: 한 데이터로부터 반경 벡터의 원 안에 포함된 데이터 벡터(점객체)
핵심백터
: n개 이상의 이웃 벡터를 갖는 데이터 벡터
직접 접근 가능
핵심 베터 p와 p의 이웃벡터 q와의 관계 p → q로 표시
접근 가능
: 어떠한 데이터 벡터와 p와 q에 대하여 직접 접근이 가능한 p → p1 → p2 → ... → q의 관계가 있다면 q는 p로부터 접근 가능 p → q로 표시(두줄 화살표)
연결 가능
: 데이터 벡터 p와 q사이에 접근 가능한 데이터 벡터 r이 존재한다면 p와 q는 서로 연결되어 있음 p↔q로 표시(두줄 화살표)
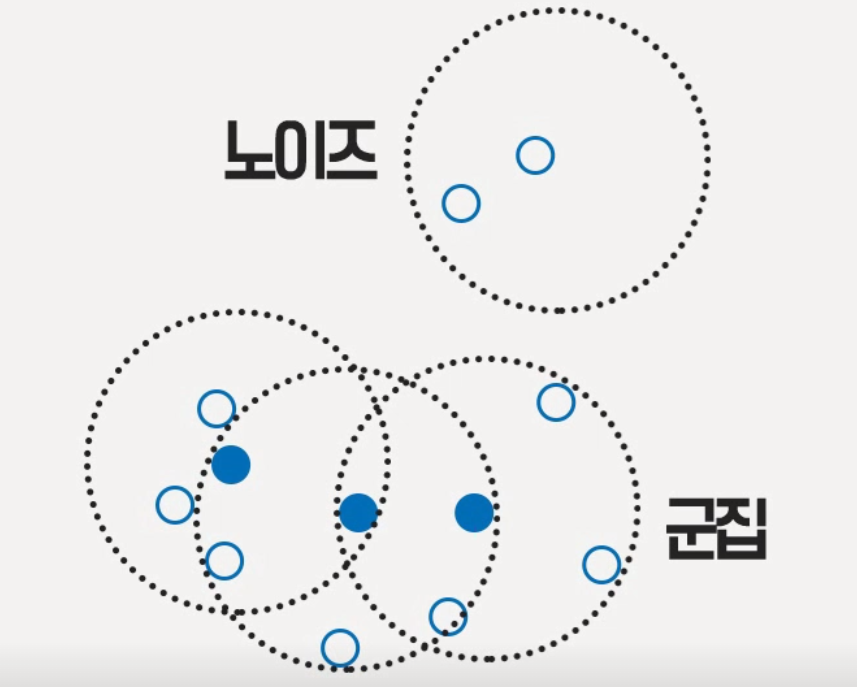
군집(Cluster)
: 한 핵심 벡터 p에 대하여 접근 가능한 모든 벡터들의 집합
노이즈
: 어떠한 군집에도 속하지 않은 데이터
DBSCAN vs k-means
- 밀도기반 vs 거리기반
- 어떤 형태의 군집도 잘 잡는 편 vs 원이나 구 모양에 최적화되어 있음
- 노이즈가 정의됨 vs 노이즈가 정의가 안됨
- 직관적 vs 수학적
- 프로그래밍으로 구현 vs 컴퓨터가 없어도 계산으로 풀 수 있음
PCA에서의 새로운 차원 k
- 고윳값 분해를 하여 가장 작으면서 분산을 많이 설명할 수 있는 상위 k개의 추상적인 축을 선택
