[RL Course] Prediction한 뒤에Model Free Control로 update하기

슥슥·2023년 4월 17일

강화학습 기초 스터디

목록 보기

7/7

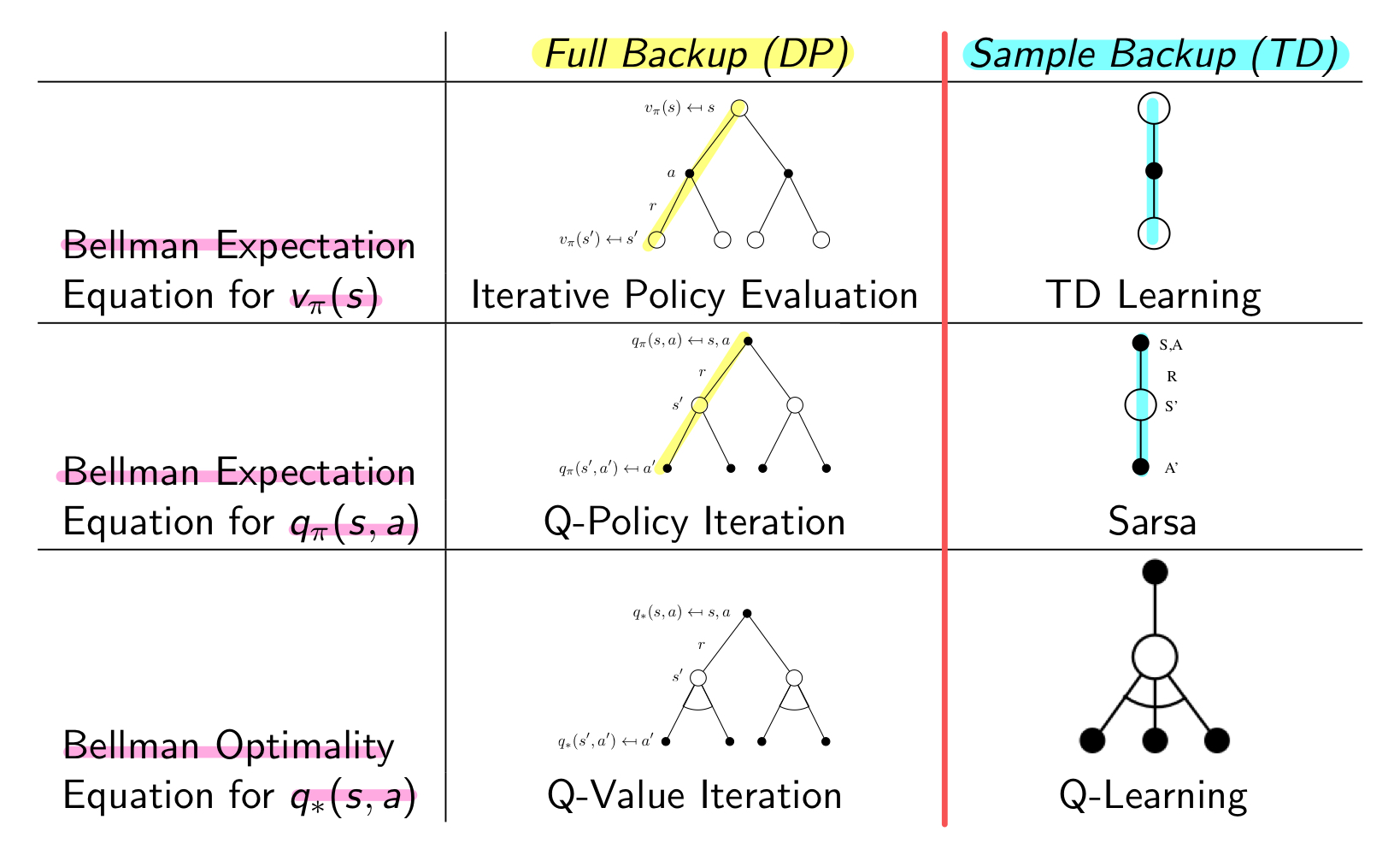
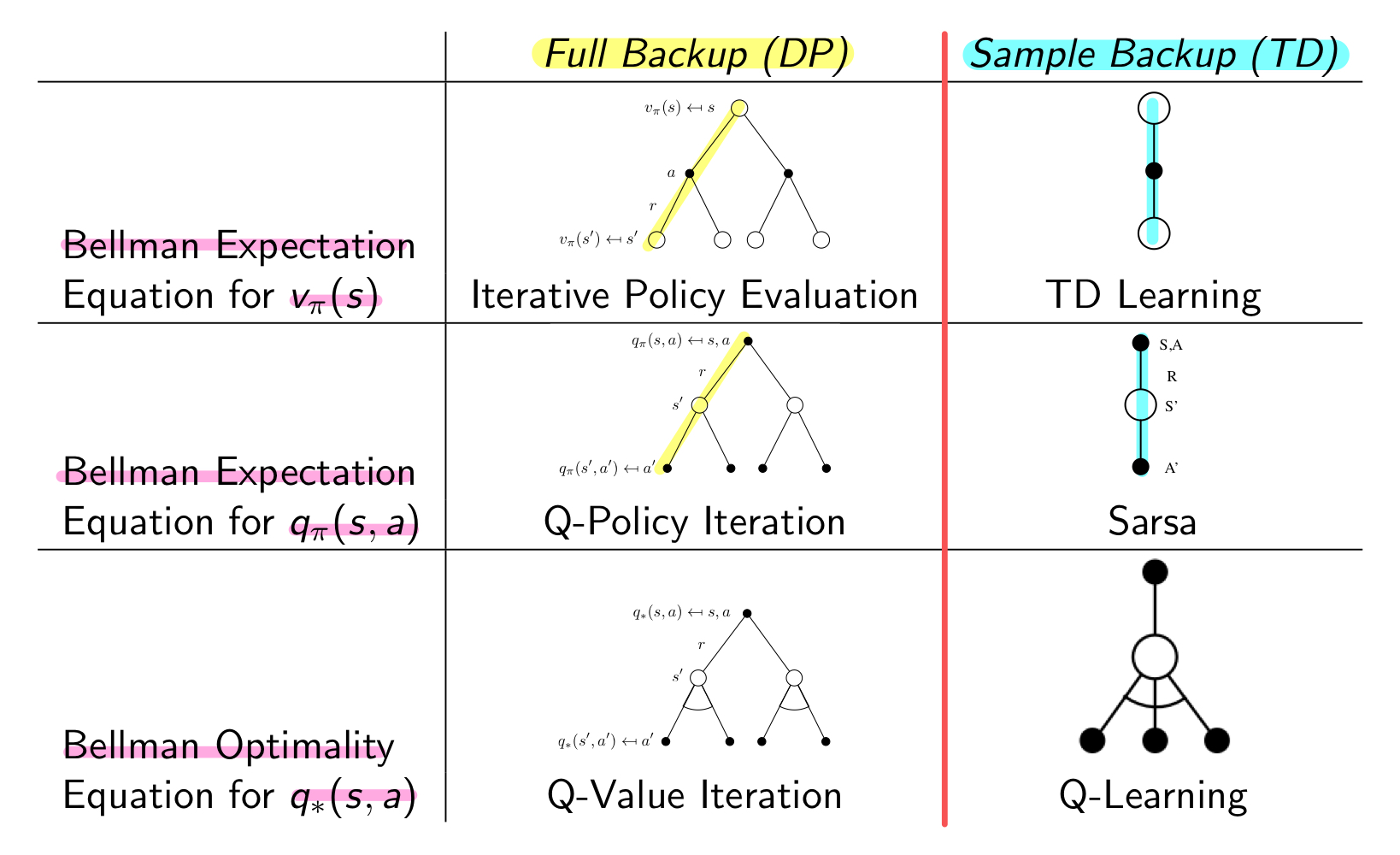
이전 게시물에서 Model Free한 Prediction을 어떻게 하는지, 즉 주어진 Policy에 대한 value function을 구하고 평가하는 방법에 대해 알아보았다. 그 과정에서 Monte-Carlo와 Temporal-Difference 방법에 대해 알아보았다.

이번에 알아볼 Model Free Control에서도 동일한 개념이 사용될 것이다. 다만, Control 과정이기 때문에 Preidction을 한 뒤에 Policy를 어떻게 개선시키는지에 대해 알아볼 것이다. 이 과정도 Model Free이기 때문에 MDP에 대한 정보 없이, agent가 경험적으로 배우게 될 것이다.

본격적으로 시작하기 전에 Off-Policy Learning과 On-Policy Learning에 대해 알아보자.

On Policy

주어진 Policy $\pi$ 를 따라 sampling 하면서 Policy $\pi$ 를 update하는 것

Off Policy

Policy $\mu$ 를 따라 sampling 하면서 Policy $\pi$ 를 update하는 것

On-Policy Monte-Carlo control

Monte Carlo로 Control 하기 이전에 처음에 DP에서 어떻게 Policy Iteration을 진행했는지 돌이켜보자.

Policy Evaluation : 주어진 policy에 대해서 $v_\pi$ 계산 ( $V=v_{\pi})$
Policy Improvement : 계산된 $v_\pi$ 에 대해 greedy한 방식으로 개선된 policy $\pi'$ 산출 (Greedy Improvement)

Exploration

Monte Carlo에서도 이런 방식의 Policy Evaluation과 Policy Improvement가 가능할까?
Problem 1. $V(s)$ 를 통해 Policy Improvement를 하기 위해서는 $P^a_{ss'}$ 과 같이 MDP의 model을 알아야한다.

\pi'(s)\ =\ \argmax_{a\in A} R^a_S\ +\ P^a_{ss'}V(s')

Problem 2. Monte Carlo는 Sampling을 통해 value function의 기댓값을 구하는 방법이기 때문에 모든 state, action에 대한 값을 볼 수 없으므로 sampling한 데이터에 대한 greedy한 방법으로 최적의 policy를 구할 수 없다.

Solution 1
첫번째 문제를 해결하기 위해 우리는 State-Value function $V(s)$ 대신 Action-Value function $Q(s,a)$ 를 사용한다. $Q(s,a)$ 를 구하고, 그에 대한 $\argmax$ 인 $a$ 가 곧 policy이기 때문에 Model Free하게 Evalution을 할 수 있다.

\pi'(s)\ =\ \argmax_{a\in A} Q(s,a)

Solution 2
두번째 문제를 해결하기 위한 가장 간단하고 효과적인 방법은 greedy하게 가지 않고, 일정 확률( $\epsilon$ )로 m개의 action 중에 random하게 선택하는 것이다.

\pi(a|s)\ = \ \begin{cases} \epsilon/m\ +\ 1\ -\ \epsilon \ \ \ \ if \ a*=\argmax_{a\in A}Q(s,a)\\ \epsilon/m \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{cases}

따라서 Monte Carlo Policy Iteration는 다음과 같은 방법으로 진행된다.

매 Episode마다,
Policy Evaluation : Monte Carlo Policy Evaluation ( $Q=q_{\pi}$ )
Policy Improvement : $\epsilon$ 확률로 다른 policy 선택하여 탐색 ( $\epsilon$ -greedy policy improvement)

그런데 여기서 하나 더 추가할 내용이 있다. 이전에 DP에서도 말했지만, Evaluation 과정에서 주어진 policy에 대한 value function이 수렴할때까지 반복할 필요가 없다. 몇번만 iteration을 진행해도, 어느정도 improvement를 위한 정보가 수집됐을 것이다.

따라서 Episode를 여러번 진행해서 Monte Carlo Policy Evaluation을 할 필요 없이, 매 Episode마다 지나온 정보를 통해 policy improvement를 하는 편이 훨씬 효율적이다. 즉, 끝까지 갈 필요 없이 가장 최근에 estimate된 value function으로 바로 policy update를 하면 된다!

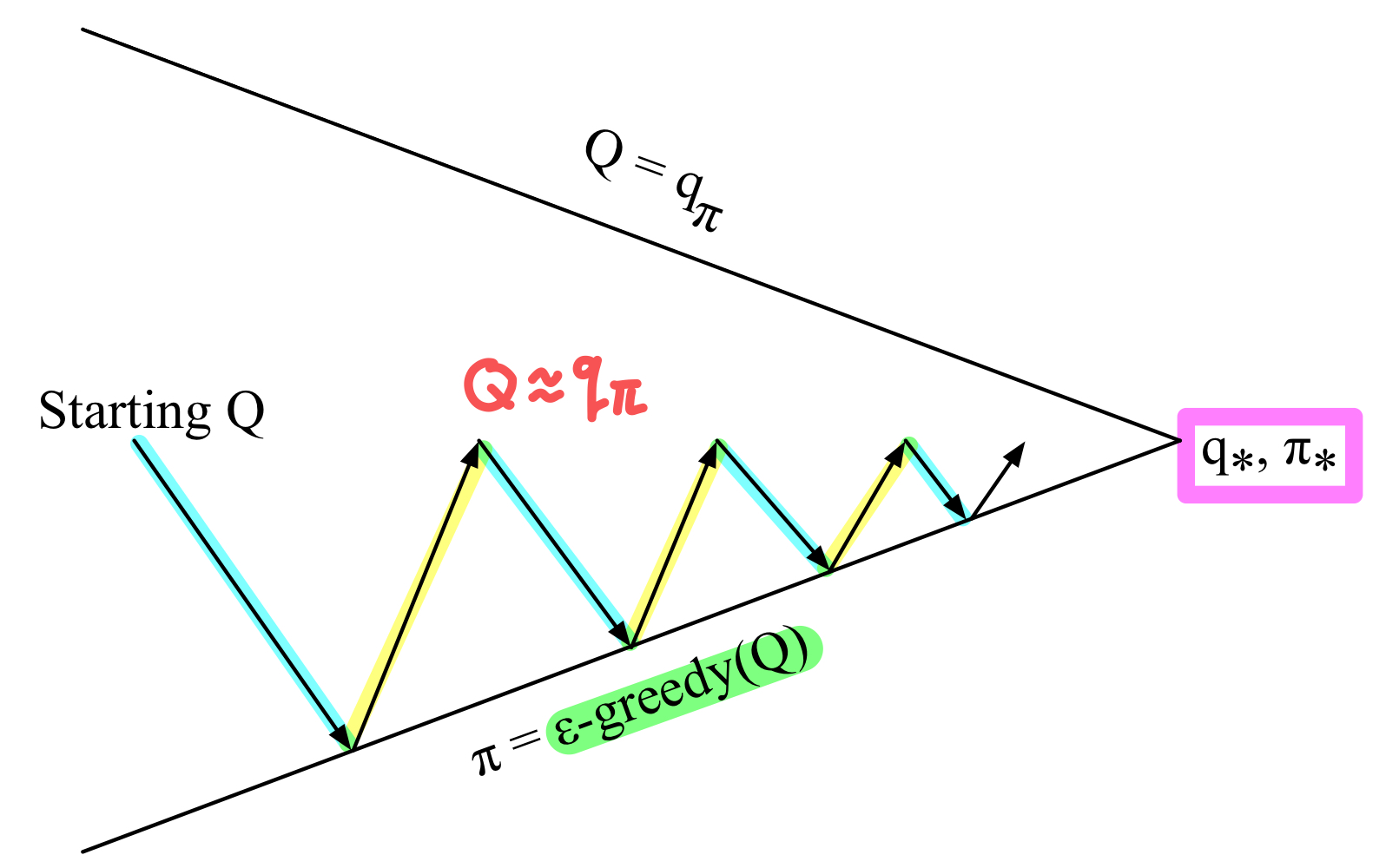
매 Episode마다,
Policy Evaluation : Monte Carlo Policy Evaluation ( $Q \approx q_{\pi})$
Policy Improvement : $\epsilon$ 확률로 다른 policy 선택하여 탐색 ( $\epsilon$ -greedy policy improvement)

GLIE (Greedy in the Limit with Infinite Exploration)

GLIE를 해석해보면 얼추, 무한한 탐색과 greedy하게 탐색, 두가지 조건이 있는 것을 볼 수 있다.

모든 State-Action pair가 무한히 여러번 탐색되어야한다.
$\lim_{k\rightarrow \infin} N_k(s,a)\ = \ \infin$

Greedy한 Policy로 수렴되어야한다.
$\lim_{k\rightarrow \infin} \pi_k(a|s)\ = \ 1(a=\argmax_{a' \in A}Q_k(s,a'))$

대표적인 예시로, $\epsilon$ -greedy 방법에서 $\epsilon$ 이 점점 0으로 수렴한다면 ( $\epsilon_k\ = \frac{1}{k}$ ) GLIE 조건을 만족한다.

GLIE Monte Carlo Control

Policy $\pi$ 를 따른 K 번째 Episode에 대해 : $\{S_1,A_1,R_2,...,S_T\} \sim \pi$
Evaluation (모든 $S_t$ , $A_t$ 에 대해 $Q(S_t,A_t)$ 를 update)
- Count : $N(S_t,A_t)\ \leftarrow \ N(S_t,A_t)+1$
- Update Value Function : $Q(S_t,A_t)\ \leftarrow \ Q(S_t,A_t)+\frac{1}{N(S_t,A_t)}(G_t-A(S_t,A_t))$
Improvement (Evaluate된 action-value function에 따라 Policy Update)
- $\epsilon \ \leftarrow \ 1/k$
- $\pi\ \leftarrow \epsilon-greedy(Q)$

On-Policy Temporal-Difference Learning

이전 게시물에서도 봤지만, TD는 MC에 비해 여러 장점이 있다. 매 Time Step마다 Online하게 update를 할 수 있고, variance도 상대적으로 작으며, 완전한 sequence가 아니어도 학습을 진행할 수 있다.

Sarsa

위에서 봤던 On-Policy MC에 TD를 대입해보자. MC의 경우에는 한 Episode에 대해 모든 state, action에 대해 update를 했다면, TD에서는 한 timestep마다의 $Q(s,a)$ 에 대해 state, action을 update할 것이다.

따라서 TD를 적용하면, Policy Evaluation 과정에서 차이가 생기게 되고, 이 방법을 SARSA라고 한다.

Q(S,A)\ \leftarrow \ Q(S,A) + \alpha(R+\gamma Q(S',A')-Q(S,A))

풀어서 설명해보면, 현재 State-Action Value Function $Q(S,A)$ 에서, 다음 step에서의 value function $Q(S',A')$ 을 반영한 Target $R+\gamma Q(S',A')$ 과의 error 방향으로 update를 진행하는 것이다.

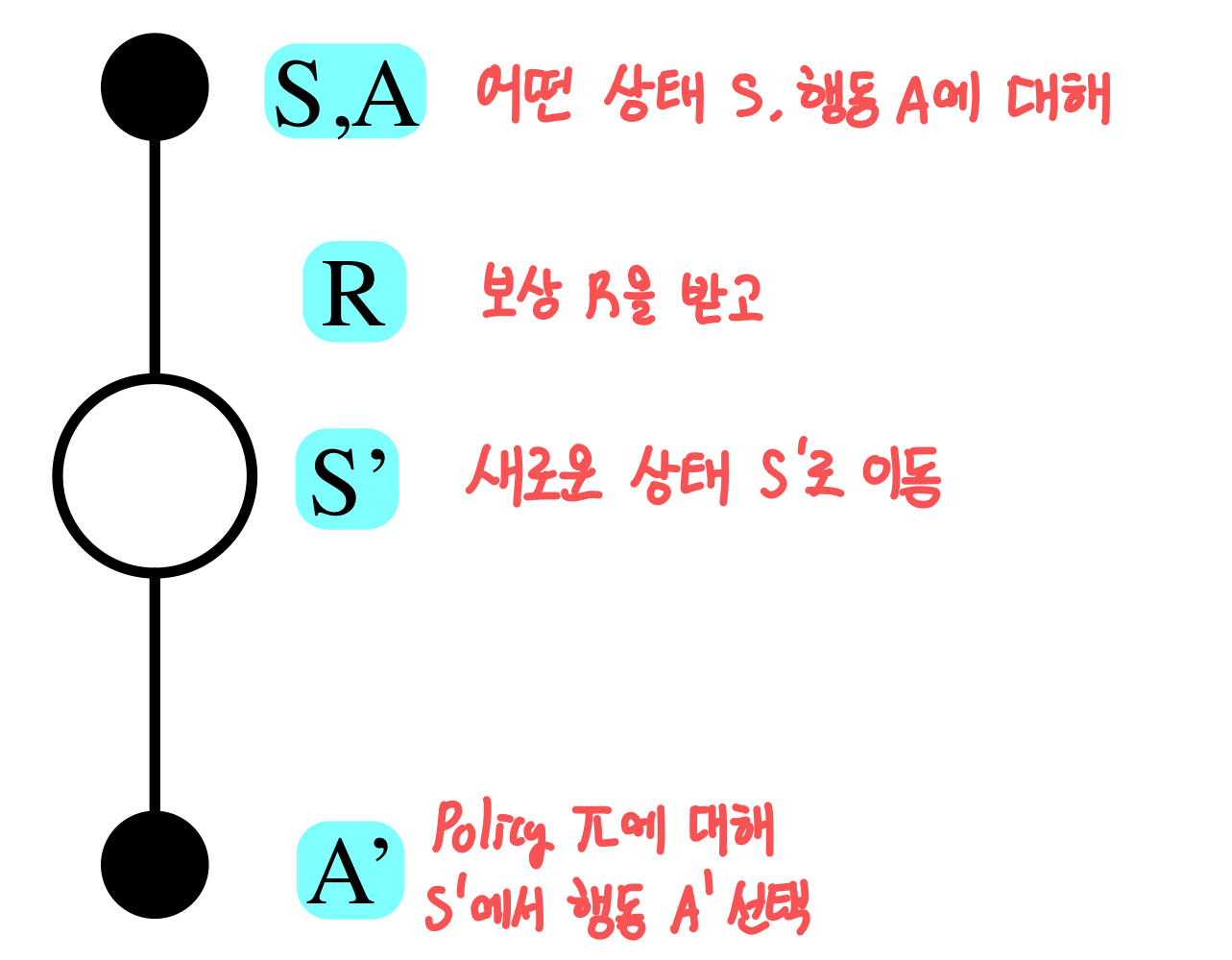
정리해보면 다음과 같다. Monte-Carlo와 유사하지만, 매 Time-Step마다 iteration을 반복하고, Sarsa를 사용해서 policy evaluation을 진행한다. Policy Improvement는 동일하게 $\epsilon$ -greedy 방식을 사용한다.

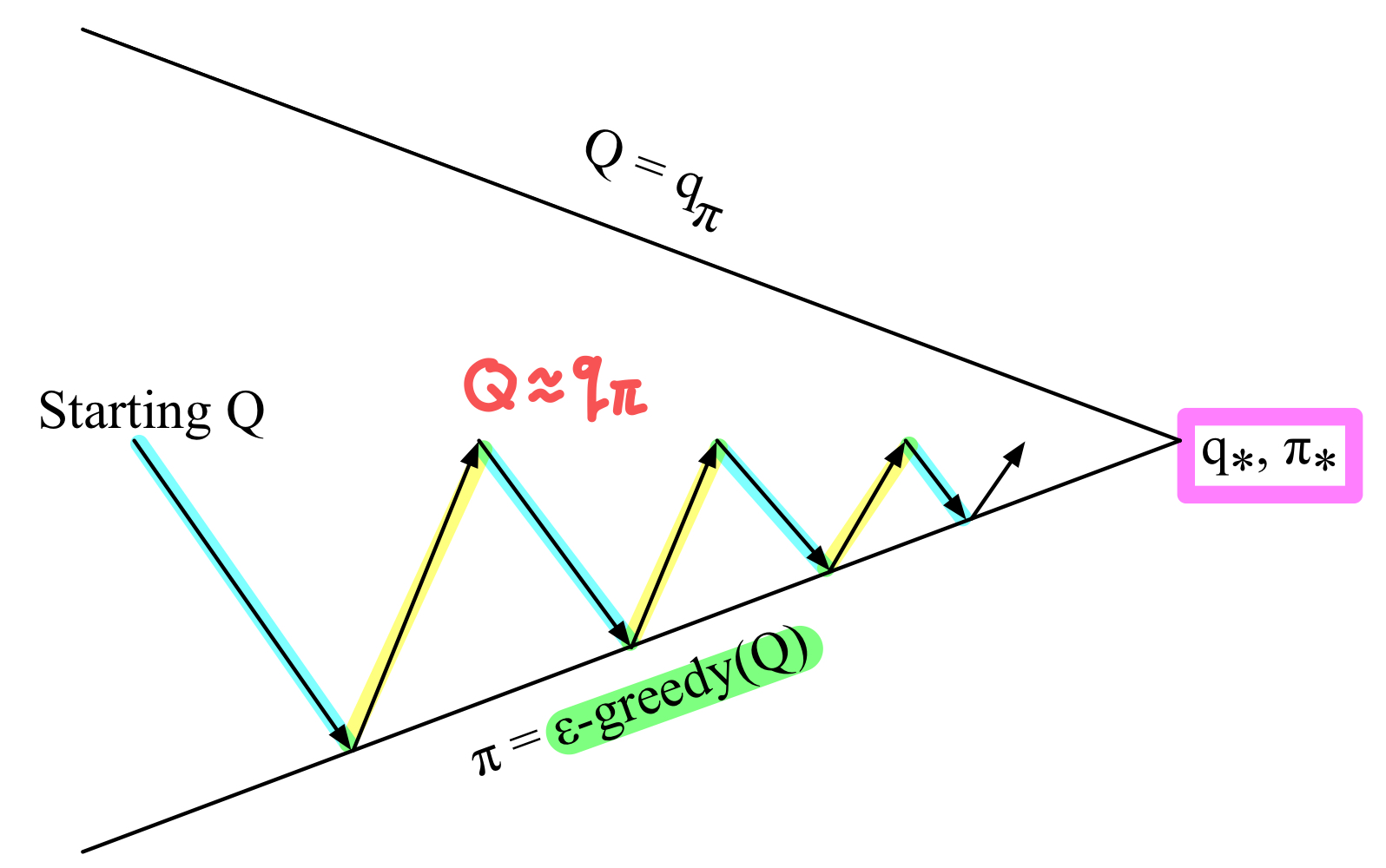
매 Time-Step마다,
Policy Evaluation : Sarsa Policy Evaluation ( $Q \approx q_{\pi})$
Policy Improvement : $\epsilon$ 확률로 다른 policy 선택하여 탐색 ( $\epsilon$ -greedy policy improvement)

Sarsa Algorithm for On-Policy Control

이 내용을 algorithm으로 풀면 다음과 같다.

읽어보면 어렵지는 않다. 매 Episode의 각 Step의 $S$ , $A$ 마다 $R$ , $S'$ , $A'$ 을 구하고 이를 바탕으로 $Q(S,A)$ 를 update하는 것이다.

Sarsa( $\lambda$ )

n-Step Sarsa

이전에 TD( $\lambda$ )에서 봤던 것처럼 Sarsa를 통한 Policy Evaluation로 여러 step을 반영해서 할 수 있을 것이다.

\begin{aligned} &n=1 \ \ \ : \ \ \ q_t^{(1)}\ =\ R_{t+1}\ +\ \gamma Q(S_{t+1}) \\ &n=2 \ \ \ :\ \ \ q_t^{(2)}\ =\ R_{t+1}\ +\ \gamma R_{t+2}\ + \gamma^2Q(S_{t+2}) \\ \\ &n=\infin \ \ \ : \ q_t^{(\infin)}\ =\ R_{t+1}\ +\ \gamma R_{t+1}\ +\ ... \ +\ \gamma^{T-1}R_T \ \ (Monte-Carlo) \\ \ \end{aligned}

이를 통해 n-step에 대한 Q-return값을 얻을 수 있다.

q_t^{(n)}\ =\ R_{t+1}\ +\ \gamma R_{t+2}\ +\ ...\ +\ \gamma^{n-1}R_{t+n}\ +\ \gamma^nQ(S_{t+n})

이렇게 estimate한 n-step뒤의 $q_t^{(n)}$ 을 target으로 하는 Sarsa Update 식을 쓸 수 있다!!

Q(S_t,A_t)\ \leftarrow \ Q(S_t,A_t)\ +\ \alpha(q_t^{(n)}-Q(S_t,A_t))

Forward View Sarsa( $\lambda$ )

Sarsa( $\lambda$ )도 이전에 봤던 TD( $\lambda$ )와 마찬가지로 Forward View와 Backward View로 설명할 수 있다.

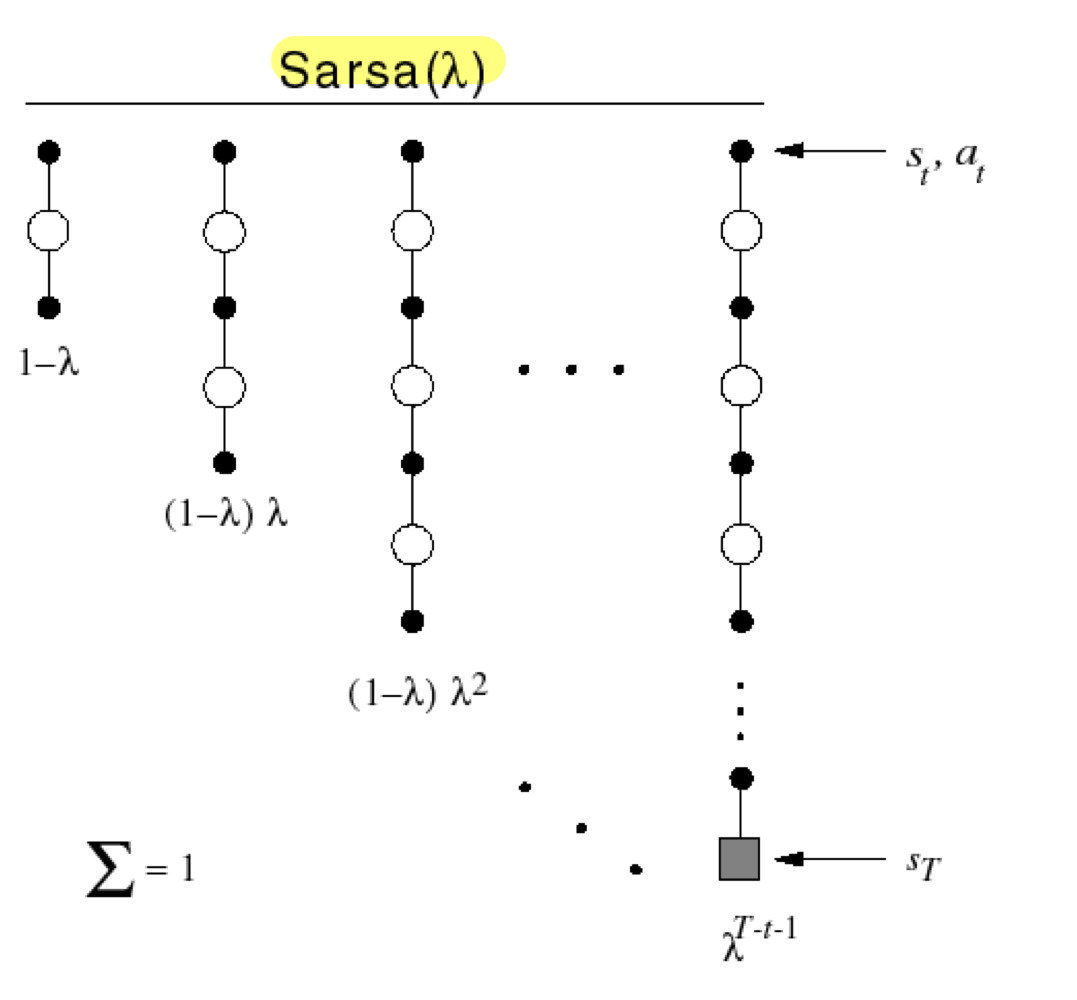
모든 n번째 step에서의 reward $q_t^{(n)}$ 를 기하 가중평균 한 $q^{\lambda}$ 를 Target으로 하는 Sarsa이다. 식으로 표현하면 다음과 같다.

q^{\lambda}\ =\ (1-\lambda)\sum^{\infin}_{n=1}\lambda^{n-1}q_t^{(n)} \\ \ \\ Q(S_t,A_t)\ \leftarrow \ Q(S_t,A_t)\ +\ \alpha(q_t^{\lambda}\ -\ Q(S_t,A_t))

말로 풀어보면, 서로 다른 time scale에서 bootstrap한 value function $q_t$ 들을 사용하여 $Q(S,A)$ 를 update하는 것이다. 그렇지만, Forward View Sarsa도 TD와 마찬가지로 $q_t^{\lambda}$ 를 구하기 위해 Episode가 끝날때까지 기다려야한다는 단점이 있다.

Backward View Sarsa( $\lambda$ )

Backward View Sarsa( $\lambda$ )에서도 Eligibility Trace의 개념이 적용된다. 이전 게시물에도 있지만, 간단하게 요약해보면 어떤 결과가 나오는데, 어떤 state, action이 얼마나 영향을 끼쳤는지를 빈도수와 최신성을 모두 고려하여 판단하는 것이다.

E_0(s,a)\ =\ 0 \\ \ \\ E_t(s,a)\ =\ \gamma \lambda E_{t-1}(s,a)\ +\ 1(S_t=s,\ A_t=a)

Eligibility Trace는 online한 update에서 사용되기 떄문에 모든 state와 action에 대해서 $Q(S,A)$ 를 update할 수 있다.

TD-error\ :\ \delta_t\ =\ R_{t+1}\ + \gamma Q(S_{t+1},\ A_{t+1})\ -\ Q(S_t,\ A_t) \\ \ \\ Q(s,a)\ \leftarrow \ Q(s,a)\ +\ \alpha \delta_tE_t(s,a)

Sarsa( $\lambda$ ) Algorithm

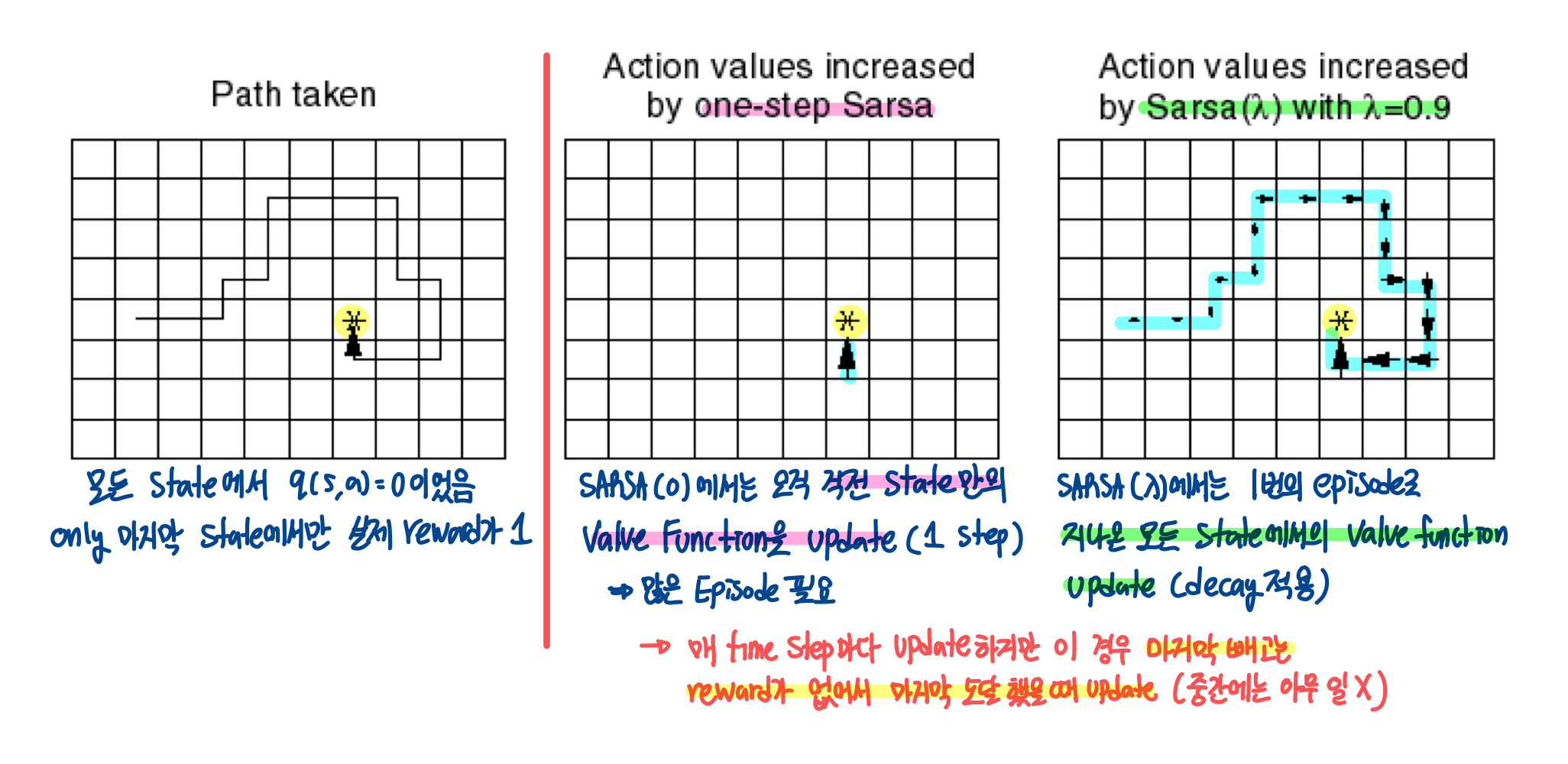
Off-Policy Learning

지금까지는 On-Policy Learning에 대해 살펴보았다. On-Policy에서는 $\pi(a|s)$ 를 학습시키기 위해 $\pi(a|s)$ 를 따랐다면, Off-Policy에서는 $\pi(a|s)$ 를 학습시키기 위해 $\mu(a|s)$ 라는 policy를 따른다.

이 방법이 중요한 이유는, 다른 Agent 혹은 사람의 행동으로부터 학습을 할 수 있다는 것이고, 다양한 policy를 탐색하면서 greedy하게 optimal한 policy를 찾아낼 수 있기 때문이다. 또한, 이전의 policy( $\pi_1, \pi_2,...\pi_{t-1}$ )를 재평가해서 학습에 사용할 수 있다. (아까 이렇게 했었는데 다르게 했으면 어땠을까?? 가 가능함 )

Importance Sampling

Importance Sampling은 효율적으로 기댓값을 추정하기 위한 방법으로, off-policy contrl이 optimal policy를 학습하는데 사용된다.

기댓값을 계산하고자하는 확률분포 $P(X)$ 를 알고 있지만, 샘플을 생성하기 어려울 경우, 상대적으로 sample 생성이 쉬운 $Q(S)$ 에서 생성된 sample을 통해 $P(X)$ 의 기댓값을 계산하는 것이다.

즉, 현재 알고자하는 데이터의 분포 $P(X)$ 에서의 Expectation을 $Q(S)$ 라는 분포에서의 sampling을 통해 추정하는 것 같다.

\begin{aligned} E_{X \sim P}[f(X)]\ &=\ \sum P(X)f(X)\ \\ \ \\ &=\ \sum Q(X)\frac{P(X)}{Q(X)}f(X) \\ \ \\ &= E_{X \sim Q}\bigg[\frac{P(X)}{Q(X)}f(X)\bigg] \end{aligned}

여기서 $f(X)$ 는 학습하고자 하는 Value Function이라고 이해하면 된다. 이 과정을 거치는 이유에 대해서는 추가적인 공부가 필요할 것 같다.

Importance Sampling for Off-Policy Monte-Carlo

Monte Carlo에서 Importance Sampling은 $\mu$ 에서 생성된 reward를 통해 $\pi$ 를 evaluate한다.
위에서 본 식에 대입해보면 Episode에 대해서 Policy $\mu$ 와 $\pi$ 사이의 유사도(Importance Sampling Ratio)를 return $G_t$ 에 반영하여 $G_t^{\pi /\mu}$ 를 구한다.

G_t^{\pi /\mu}\ =\ \frac{\pi(A_t|S_t)}{\mu(A_t, S_t)} \frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}, S_{t+1})}...\frac{\pi(A_T|S_T)}{\mu(A_T, S_T)} G_t

이렇게 수정된 return을 target을 향해 update를 진행하게 된다.

V(S_t)\ \leftarrow \ V(S_t)\ +\ \alpha \Big(\textcolor{red}{G_t^{\pi /\mu}}\ -\ V(S_t)\Big)

이러한 방식은 딱 봐도 굉장히 문제점이 많은데, 모든 step에 대해서 policy 사이의 Ratio를 고려하기 때문에 Variance가 극단적으로 증가한다.

Importance Sampling for Off-Policy TD

TD에서도 마찬가지로 $\mu$ 에서 생성된 reward를 통해 $\pi$ 를 evaluate한다. 그대신 MC의 reward $G_t$ 대신 TD reward인 $R+\gamma V(S')$ 에 유사도(Importance Sampling Ratio)를 1 Step 단위로 반영한다.

V(S_t)\ \leftarrow \ V(S_t)\ +\ \alpha \Big(\textcolor{red}{\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1}+\gamma V(S_{t+1}))}\ -\ V(S_t)\Big)

TD는 Episode내 모든 policy에 대해서 ratio를 반영하는 것이 아니라, 1 step 단위로 반영하기 때문에 MC에 비해 Variance가 낮다. 사실상 의미가 없다고 보면 된다.

Q-Learning (SARSAMAX)

Importance Sampling을 사용하지 않고 Off-Policy를 적용하기 위해 등장한 개념이 Q-Learnig이다.

Q-Learning에서는 action value function $Q(s,a)$ 를 기반으로 학습하며 2개의 Policy가 사용되고 각각 역할이 다르다.

Behaviour Policy $\mu$

$A_{t+1}\ \sim \ \mu(\cdot |S_t)$

다음 action을 선택하는 실제 policy

$\epsilon$ -greedy

Target(Alternative) Policy $\pi$

$A'\ \sim \ \pi(\cdot|S_t)$

Reward를 구하고 Update를 할 때에 다음 state $S'$ 에서 다음 action $A'$ 을 선택하는데 고려하는 가상의 policy

greedy

$\pi(S_{t+1})\ =\ \argmax_{a'}Q(S_{t+1},\ a')$

$Q(S_t,A_t)$ 는 Target Policy, 즉 Alternative Policy에 대한 value $R_{t+1}\ +\ \gamma Q(S_{t+1},\ A')$ 를 target으로 update된다.

Q(S_t,\ A_t)\ \leftarrow \ Q(S_t,\ A_t)\ +\ \alpha(\textcolor{red}{R_{t+1}\ +\ \gamma Q(S_{t+1},\ A')}\ -\ Q(S_t,\ A_t))

여기서 $\epsilon$ -greedy, greedy한 Policy Evaluation을 적용하면 다음과 같이 식을 단순화 시킬 수 있다.

\begin{aligned} R_{t+1}\ &+\ \gamma Q(S_{t+1},\ A') \\ =\ R_{t+1}\ &+\ \gamma Q(S_{t+1},\ \argmax_{a'}Q(S_{t+1},\ a')) \\ =\ R_{t+1}\ &+\ \max_{a'}\gamma Q(S_{t+1},\ a') \end{aligned}

말로 풀어서 설명을 해보자면, $A'$ 은 Target Policy를 따르기 때문에 greedy한 action을 선택하므로 $\argmax_{a'}Q(S_{t+1},\ a'))$ 로 치환할 수 있다.

Q(S,\ A)\ \leftarrow \ Q(S,\ A)\ +\ \alpha \Big(R\ +\ \gamma \max_{a'}Q(S',\ A')\ -\ Q(S,\ A)\Big)

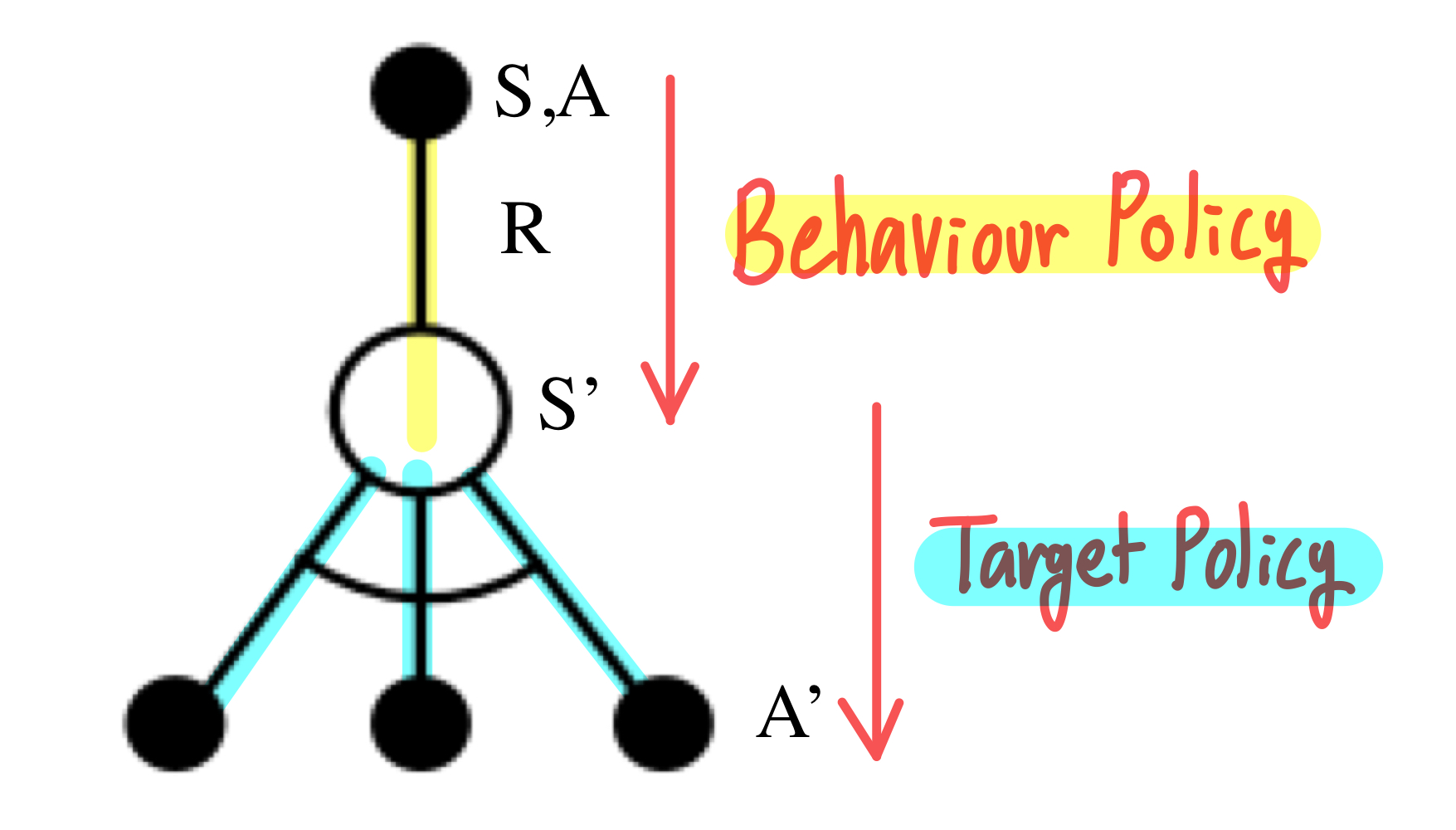
SARSA하고 거의 비슷해보이는데 무슨 차이가 있을까? SARSA에서는 정해진 policy $\pi$ 에 대해서 policy iteration을 하지만, Q-Learning에서는 $\argmax$ 된 policy $\pi*$ 를 바탕으로 policy iteration을 한다.

좀 더 단순하게 얘기하면, Q-Learning(SARSAMAX)에서는 Behaviour Policy로 다음 state를 얻고, Target Policy를 통해서 실제 Target을 구한다.

SARSA\ :\ Q(S_t,A_t)\ \leftarrow\ \alpha \Big(R_{t+1}\ +\ \gamma \textcolor{red}{Q(S_{t+1},A_{t+1})}\ -\ Q(S_t,A_t))\Big)\ \\ \ \\ Q-Learning\ :\ Q(S_t,A_t)\ \leftarrow\ \alpha \Big(R_{t+1}\ +\ \gamma \textcolor{red}{\max_{a'}Q(S_{t+1},a')}\ -\ Q(S_t,A_t))\Big)

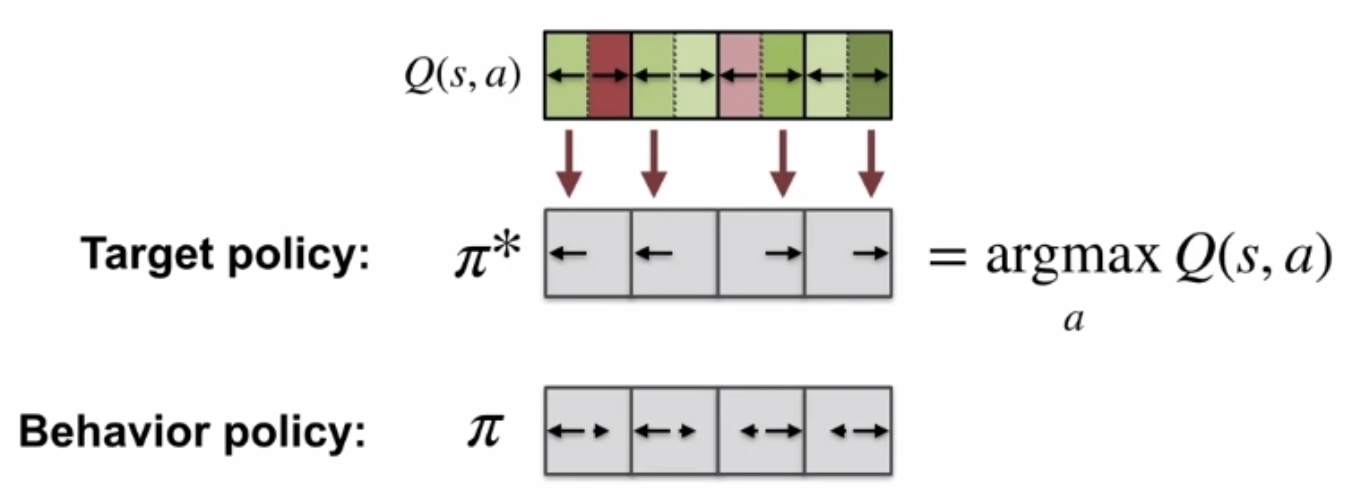
식을 조금만 직관적으로 이해해보면, SARSA는 현재 상태에서 action을 선택한 뒤에, 다음 상태에서도 동일한 policy를 통해 target을 구하지만, Q-Learning에서는 다음 상태에서 Target Policy에 따라 Optimal한 값을 target으로 update한다.

Summary

슥슥

이전 포스트