앞에서는 Dynamic Programming(Policy Iteration, Value Iteratoin)을 통해 MDP를 어떻게 해결하는지 살펴봤다. 모든 state와 action을 살펴보면서 Bellman Equation을 사용해서 최적의 policy를 찾았는데, 이건 MDP에 대한 모든 정보를 알고있을때에만 가능하다.

그렇지만, 실생활의 많은 문제에서는 Environment가 어떻게 작동하는지 알 방법이 없다. 이런 문제 때문에 등장한 개념이 Model Free RL이다. Model Free하다는 것은 MDP에 대한 정보없이, Agent의 경험이나 environmen와의 상호작용을 바탕으로 직접 value function, policy를 도출한다는 것이다.

DP에서처럼, Model Free한 방법으로 Prediction은 어떻게 하는지, 그리고 Control은 어떻게 하는지 하나씩 알아보자.

이번 게시물에서 살펴볼 Model Free Prediction은 MDP에 대한 정보 없이 현재의 Policy의 Value Function을 도출해서 현재의 policy를 Evaluation하는 과정이다.

Monte-Carlo Policy Evaluation

Monte Carlo 방법은 이전 게시물에서도 봤었지만 Sampling을 통해 직접 학습하는 방법이다. 그 Sampling이란 한번의 Episode를 온전히 진행하는 것이기 때문에, 반드시 Episodic한 MDP에서 적용만 가능하다.

DP에서 봤던 Policy Evaluation을 다시 한번 상기시켜보자. Policy Evaluation을 통해 얻고 싶은건, 현재 policy를 따랐을 때 얻을 수 있는 return들의 기댓값 $v_\pi(s)$이고 $v_\pi(s)\ =\ E_\pi[\ G_t\ |\ S_t=s\ ]$ 로 표현할 수 있다. 기존에는 모든 경우를 고려해서 수식적으로 update 했다면, Monte Carlo에서는 경험적인 평균(empirical mean)으로 Expectation을 대체한다. 조금 구체적으로 살펴보면 2가지 방법이 있다.

First Visit MC Policy Evaluation

어떤 episode에서 상태 $s$에 대한 value function을 update할 때, 해당 episode에서 $s$를 처음 방문한 시점만을 고려해서 update하는 방법이다.

풀어서 설명을 해보자면, 어떤 episode에서 상태 $s$를 처음 방문하는 시점 t에 대해,
누적 방문 횟수 : $N(s)\ \leftarrow \ N(s)+1$
누적 return : $S(s)\ \leftarrow \ S(s)+G_t$
추정 Value : $V(s)\ =\ S(s)/N(s)$
충분히 많은 episode를 거친다면, $V(s)$는 참 value function $v_\pi(s)$에 수렴할 것이다.

Every Visit MC Policy Evaluation

First Visit과 다르게 어떤 episode에서 상태 $s$에 대한 value function을 update할 때, 해당 episode에서 $s$를 방문한 모든 시점을 고려해서 update하는 방법이다.

풀어서 설명을 해보자면, 어떤 episode에서 상태 $s$를 방문하는 모든 시점 t에 대해,
누적 방문 횟수 : $N(s)\ \leftarrow \ N(s)+1$
누적 return : $S(s)\ \leftarrow \ S(s)+G_t$
추정 Value : $V(s)\ =\ S(s)/N(s)$
충분히 많은 episode를 거친다면, $V(s)$는 참 value function $v_\pi(s)$에 수렴할 것이다.

Incremental Monte Carlo

Incremental Mean은 말 그대로 누적해서 평균을 구하는 것이다. Monte Carlo에서 매번 새로운 return 값이 생길때마다 전체의 평균을 구하는 방법이다!!

일반적으로 sequence $(x_1, x_2, x_3, ...)$에 대해서 Incremental Mean$(\mu_1, \mu_2, \mu_3, ...)$은 다음과 같이 구할 수 있다.

말로 풀어보면, k번째 mean은 k-1번째 mean + $\frac{1}{k}$ (k번째 관측치 - k-1번째 mean) 으로 구할 수 있다!!

이 원리를 Monte Carlo에 적용하면 어떻게 될까??

Monte Carlo에서는 한 Episode $<S_1, A_1,R_2,S_2,...,S_T>$를 모두 진행한 뒤에 Value Function $V(s)$를 누적 평균해서 update한다. Episode에서 방문한 상태 $S_t$에 대한 return이 $G_t$, 방문횟수가 $N_t$라면 value function $V(S_t)$는 다음과 같이 update할 수 있다.

위에서 말로 풀어본 것에 대입해보면, 기존의 value function $V(S_t)$와 기존의 value function과 현재 단계에서 직접 산출된 reward의 차이 $\frac{1}{N(S_t)} (G_t\ -\ V(S_t))$를 더해서 value function을 업데이트한다.

좀 더 직관적으로 이해해보면, 기존의 value function를 가장 최근에 산출된 reward와의 error 방향으로 update하는 것이라고 볼 수도 있다.

Temporal-Difference Policy Evaluation

여러번 Episode를 진행해서 value function을 evaluate하는 Monte Carlo의 본질적인 문제점 중에 하나는 Episode를 끝까지 진행을 한 뒤에야만 update를 할 수 있다는 점이다.

Temporal Difference 방법은 이와 다르게 Episode를 끝까지 진행하지 않고, 진행하는 도중에 time step에 따라서 update를 진행할 수 있다.
큰 차이점은 Monte Carlo는 Episode를 끝까지 진행해서 계산한 값을 보고 update 하는것이고, Temporal Difference는 Episode 도중에 update를 하기 때문에 예측값을 보고 update를 진행한다. 이 방법을 bootstrapping이라고 한다.

Monte Carlo(MC) VS Temporal Difference(TD)

일단 강의를 듣고 이해한대로 그림으로 그려봤다.

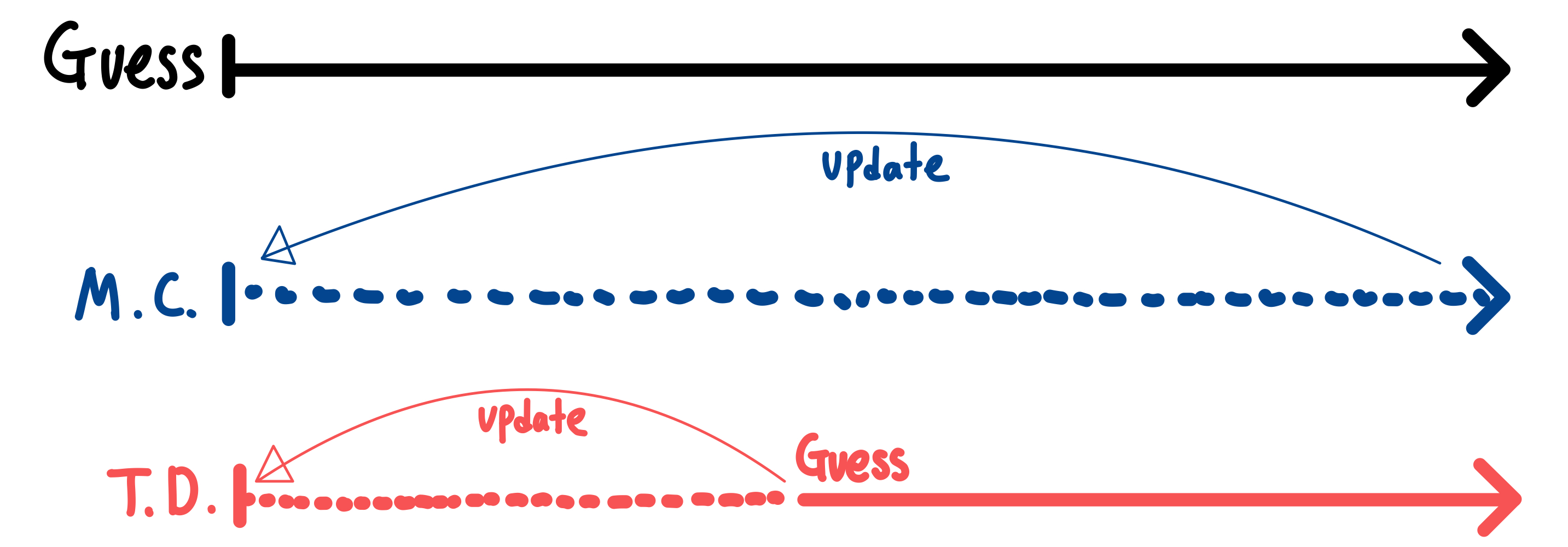
우선, MC와 TD 모두 목표는 주어진 policy $\pi$에 대해서, 참 value function $v_\pi$를 Evaluate 해내는 것이다. 차이는 어떤 값을 target으로 학습하는지에 있다.

Every Visit MC

MC에서는 실제 return $G_t$를 토대로 $V(S_t)$를 update한다.

TD(0)

TD에서는 다음 step에서의 추정된 return $R_{t+1}\ +\ \gamma V(S_{t+1})$ 를 토대로 $V(S_t)$를 update한다.

이 식을 말로 풀어서 써보면 기존의 value function를 다음 step의 value function과 Reward의 합과의 error $\delta$ 방향으로 update하는 것이라고 볼 수도 있다.

Example

다음 예시를 보면 좀 더 직관적으로 이해할 수 있다.주어진 문제 상황은 사무실에서 나와서 집으로 가는 아주 간단한 한가지 sequence에 대해 나타낸 것이다.

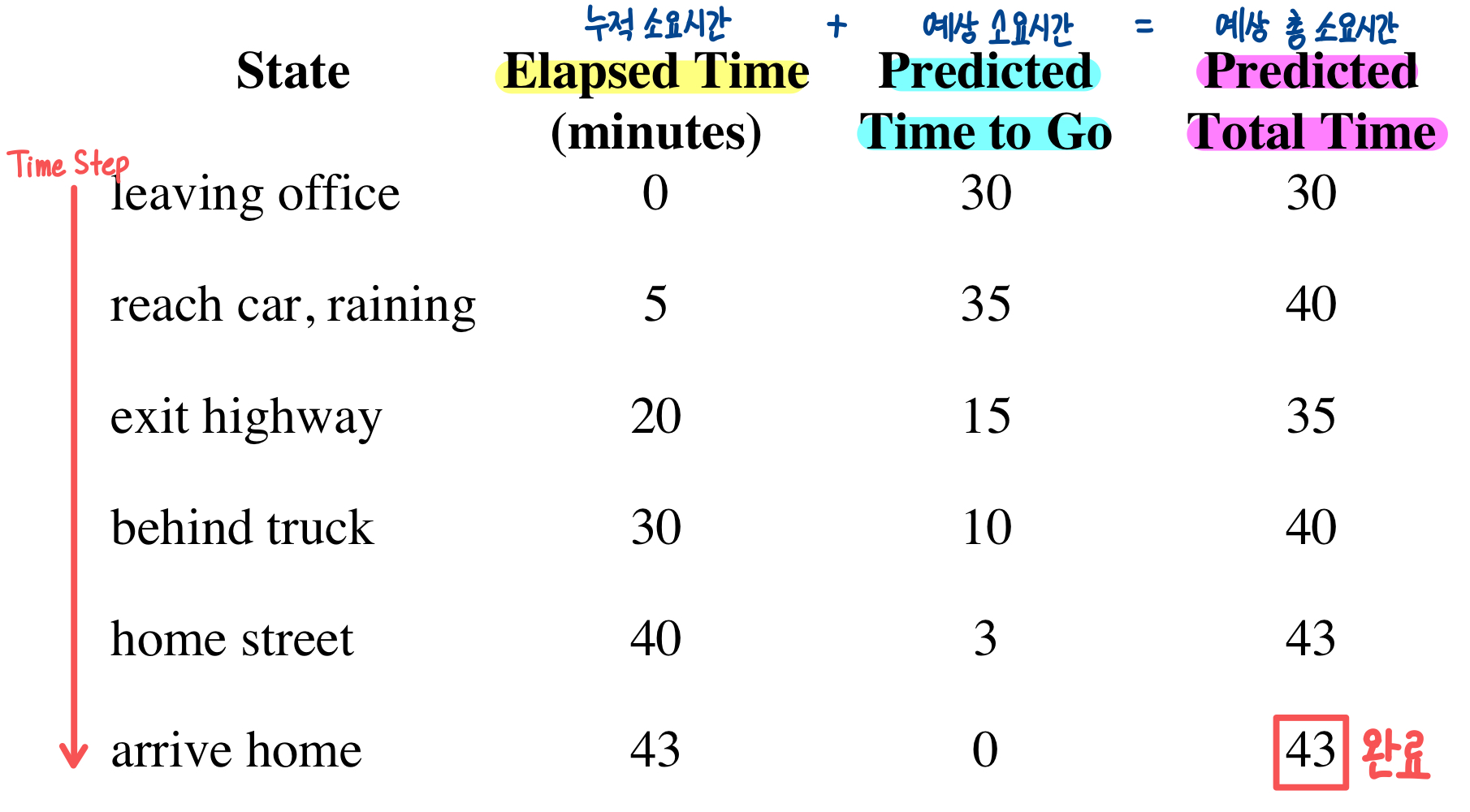
이런 문제 상황에 대해 MC와 TD가 어떻게 Target에 가까워지는지 살펴보자.

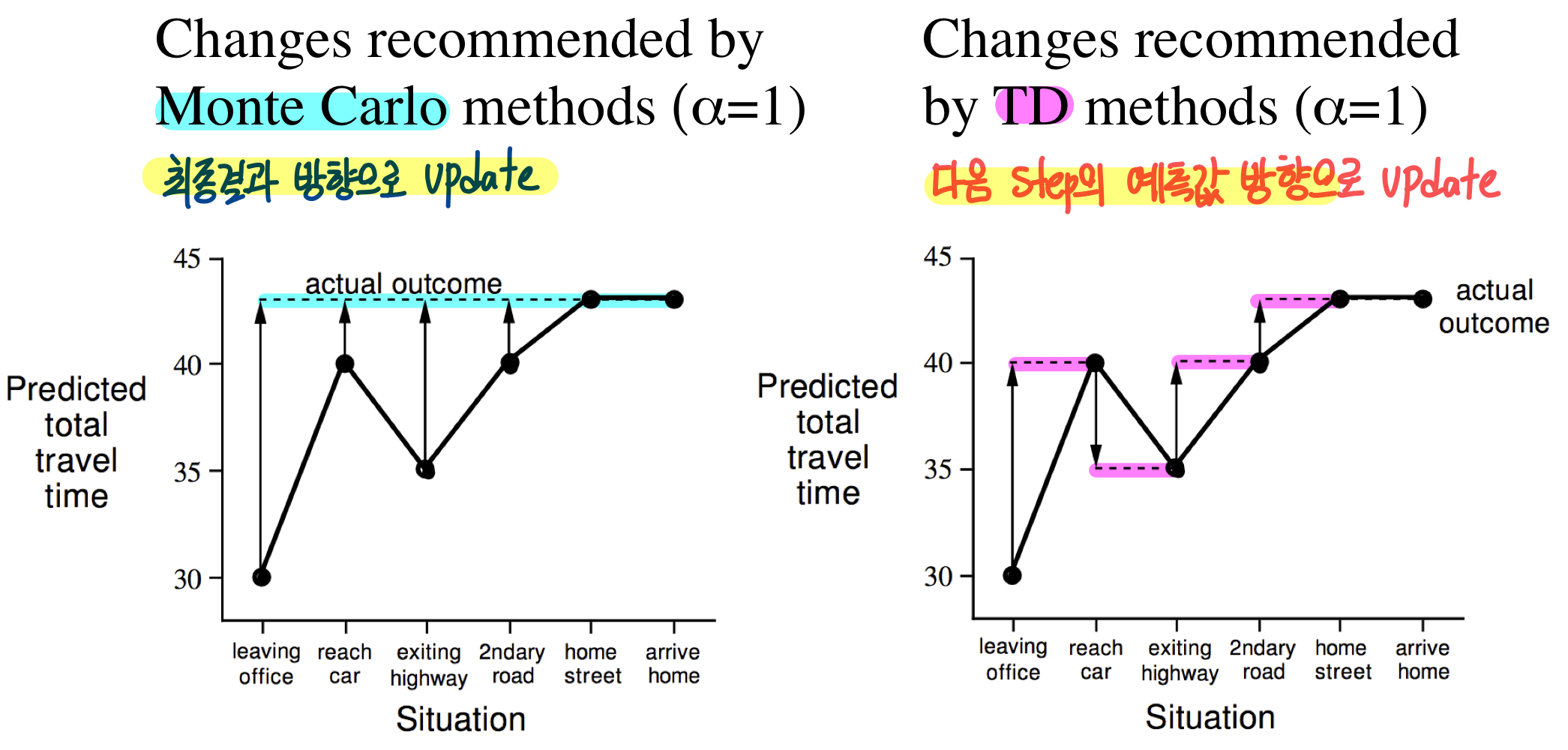
MC의 경우에는 sequence를 다 수행한 결과, 즉 "43분"을 기준으로 한다면, TD에서는 각 time step마다 다음 time step에서의 상태를 기준으로 한다.
예를 들어 "reach car, raining"이라는 상황에서는 "40분"으로 예측을 했지만, 다음 time step인 "exiting highway"의 예측값인 "35분"을 target으로 학습을 한다.
이 예시가 딱 들어맞는 예시는 아니지만 개념적으로 그렇구나~~ 정도로는 괜찮은 것 같다.

Monte Carlo	Temporal Difference
Episode가 완료되고, return이 나온 후에 학습 가능	Final Outcome 이전에 학습 가능 (each time step)
완전한 Sequence 필요 (Episodic Environment)	완전한 Sequence 없이 학습 (Countinuing Environment)
초기값에 덜 민감함	초기값에 민감함
High Variance & Low Bias	Low Variance & Some Bias
Does not Exploit Markov Property	Exploits Markov Property
Minimum MSE로 수렴(관측된 return에 수렴하도록)	Max likelihood Markov Model로 수렴(데이터를 잘 설명하는 MDP 해결)
$\ \sum_{k=1}^{K}\sum_{t=1}^{T_k}(G_t^k-V(s_t^k))^2$	$\hat{P^a_{ss'}} =\frac{1}{N(s,a)}\sum_{k=1}^{K}\sum_{t=1}^{T_k}1(s_t^k,a_t^k,s_{t+1}^k=s,a,s') \\ \ \\ \hat{R^s_a}=\frac{1}{N(s,a)}\sum_{k=1}^{K}\sum_{t=1}^{T_k}1(s_t^k,a_t^k=s,a)r_t^k$
Bootstrap X, Sampling O	Bootstrap O, Sampling O

Bias & Variance

위의 표에서 bias 와 variance에 대한 얘기가 나오는데 잠깐 짚고 넘어가보자.

TD는 바로 다음 step과의 error만 고려하여 update를 하기 때문에 학습에 시간이 많이 소요되고 학습이 한쪽으로 치우쳐 지게 된다. TD가 학습을 할 때에 target으로 삼는 value function $V(S_{t+1})$은 실제 reward의 값을 반영한 값이 아니라, 결국 추정한 값에 불과하고, 실제 environment에서 얻게되는 정보는 즉시 보상받는 reward인 $R_{t+1}$일 뿐이다. 따라서 TD는 상대적으로 bias가 높다.

반면, MC는 episode가 끝나야만 update를 할 수 있지만 episode가 끝난 뒤에는 실제 얻은 reward의 정보를 반영할 수 있다. 하지만, 동일한 state에서 시작하더라도 episode를 어떻게 거쳤는지에 따라 다른 value function으로 update될 위험이 있다. 따라서 MC는 variance가 높다.

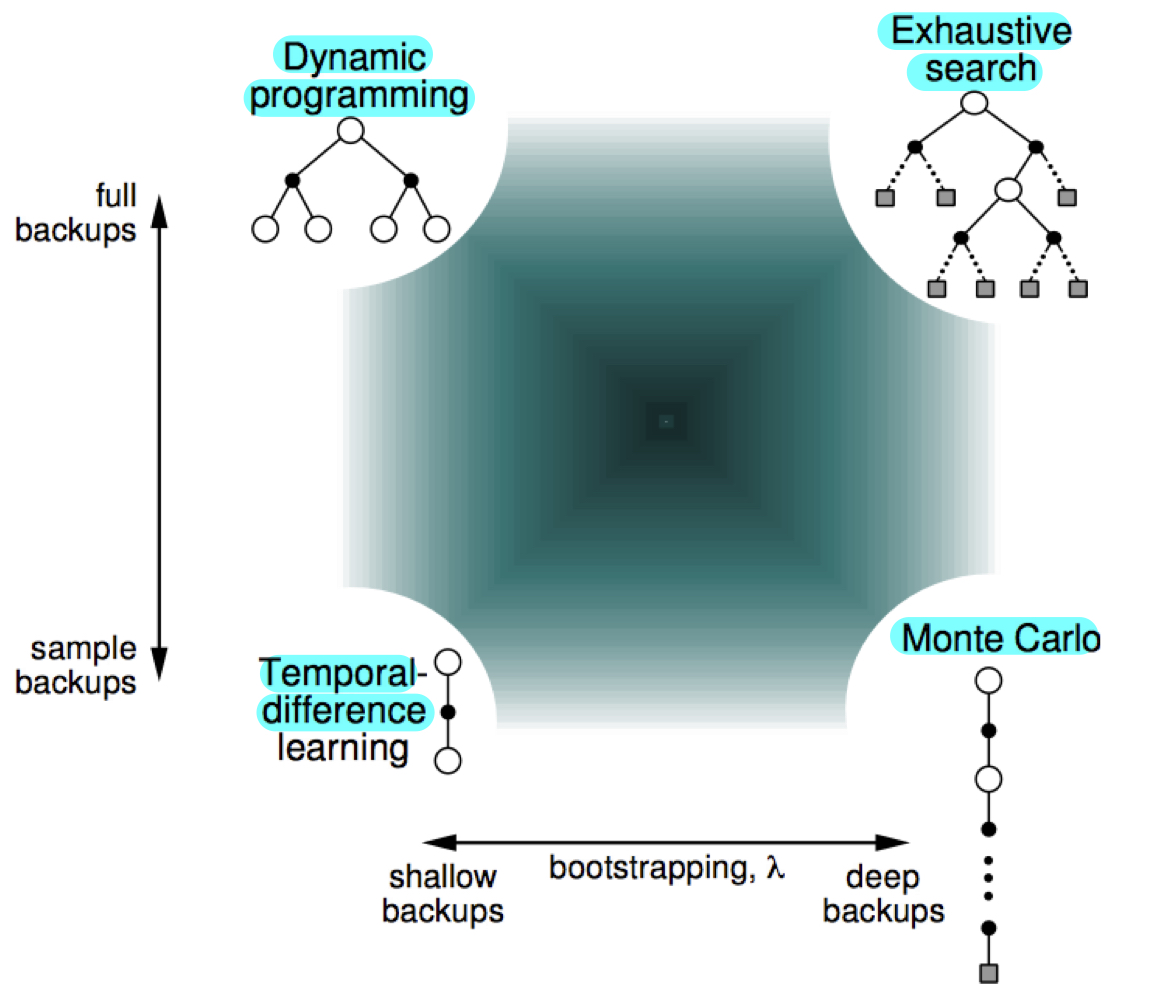
Bias와 Variance는 서로 trade-off 관계에 있으며 강화학습에서 학습에 방해되는 요소들입니다. 따라서 이를 줄이기 위해 MC와 TD의 장점을 살리기 위한 방법들이 연구되었습니다. MC와 TD의 중간 지점을 택하고자 하는 것이 다음에 살펴볼 $TD(\lambda)$이다.

TD($\lambda$)

n-Step TD

위에서 TD를 배울 때에는 1step 뒤의 value function만 고려해서 현재 값을 update했다. 이로 인해서 TD는 bias가 상대적으로 높다는 단점이 있다. 이를 해결하기 위해서는 좀 더 많은 실제 보상$R$을 탐색할 필요가 있다. 즉, 1step이 아니라 n step 뒤의 value function에 대한 예측값을 target으로 update하면 좀 더 많은 environment의 피드백을 반영할 수 있을 것이다.

만약, n이 무한히 증가해서 Episode의 마지막까지 진행된다면, 그 경우에는 Monte Carlo와 같은 의미를 가질 것이다.

이를 통해 n-step 뒤의 value function을 고려한 n-step return 값 $G_t^{(n)}$을 계산할 수 있다.

이 식을 똑같이 적용하여 $G_t{(n)}$을 target으로 하는 TD update 식을 쓰면 다음과 같다.

그렇다면 어떤 n, 즉 얼마 뒤의 시점까지의 value function을 기준으로 update를 해야할까??

이 고민에서 나온 아이디어가, TD($\lambda$)인데, Forward View와 Backward View로 구분할 수 있다.

Forward View of TD($\lambda$)

Forward View of TD($\lambda$)는 n-step 동안의 reward를 기하 가중 평균 (Geometric Weighted Average)를 사용하여 update하는 것이다. 여러 step에 대한 평균을 구해서 target으로 삼는다면, n이 작을때와 n이 클때의 장점을 모두 취해서 update할 수 있을 것이다!!

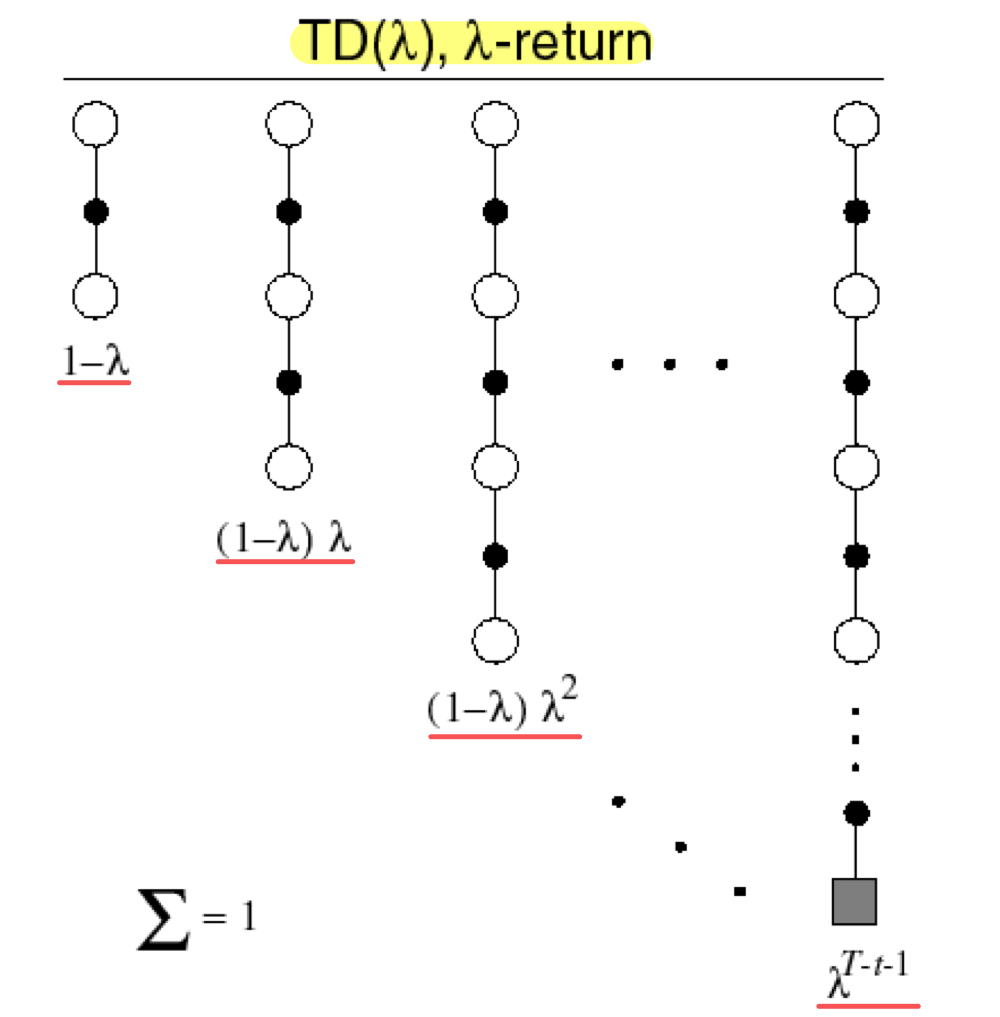
n-step마다 얻어진 return에 이 weight을 곱하여 λ-return($G_t^λ$)을 만들고, 이 return으로 update를 하면 forward-view TD($\lambda$) 가 된다. 구체적인 식은 다음과 같다.

Forward View 같은 경우에는 $G_t^{\lambda}$를 계산하기 위해 미래 시점의 return들을 사용한다. 앞서 살펴본 TD에서는 다음 step의 value function 만 사용하기 때문에 λ=0이고, λ=1이면 나머지 weight은 모두 0가 된다.
그런데 이렇게 되면 다시 episode가 끝나야 update를 할 수 있다는 MC에서의 단점이 다시 발생하게 된다.

Backward View of TD($\lambda$)

그럼 TD($\lambda$)의 원리를 유지하면서 매 time step마다 update를 진행할 수 있는 방법을 생각해봐야한다. 여기서 알아야할 개념이 Eligibility Trace이다.

Eligibility Trace

어떤 사건이 발생했다고 생각해보자. 예를 들어 종이 3번 울리고, 알람이 한번 울리더니 전기 충격이 왔다고 가정해보자. 그럼 전기 충격이 발생하게한 요인은 무엇이었을까? 빈도수를 생각하면 종이 울리는 것, 최신성을 생각하면 알람이 울리는 사건이 전기 충격을 발생시켰다고 해석할 수 있다. Eligibility Trace는 이런 Frequency와 Recency를 모두 고려하여 과거 사건을 추적하는 것이다.

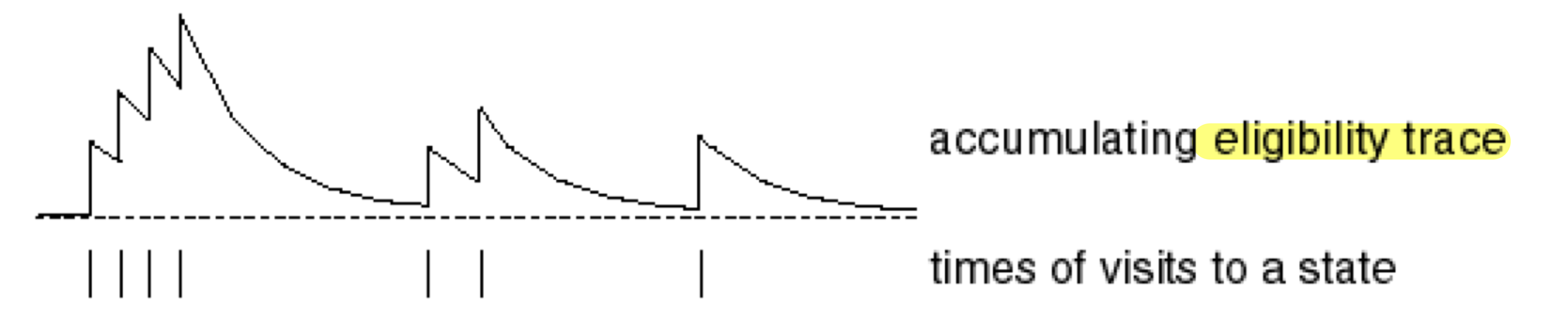
위 그래프를 보면 사건이 발생할때마다 급격한 상승이 발생하고, 시간이 지날수록 점차 그 정도가 약해지는 것을 볼 수 있다. 이 과정을 식으로 나타내면 다음과 같다.

식을 해석해보자면, 매 timestep마다 $\gamma$씩 decay가 발생하지만, $s$가 발생하면 1만큼 증가하여 최근에 일어날수록 값이 크고, 자주 발생할수록 값이 큰 Eligibility Trace 값이 나옴을 알 수 있다.

Backward View of TD($\lambda$)

Backward View에서는 특정 시점을 기준으로, 모든 state에 대한 eligibility trace를 고려하여 update를 진행한다.
앞에서 살펴보았던 TD식에 Eligibility Trace 값이 반영된 것으로, 다음과 같다.

식을 보면 기존의 TD와 동일하게 TD-error 방향으로 update를 진행하지만, 뒤에 $E_t(s)$가 붙어서 Eligibility Trace를 통해 보정하는 것을 볼 수 있다.

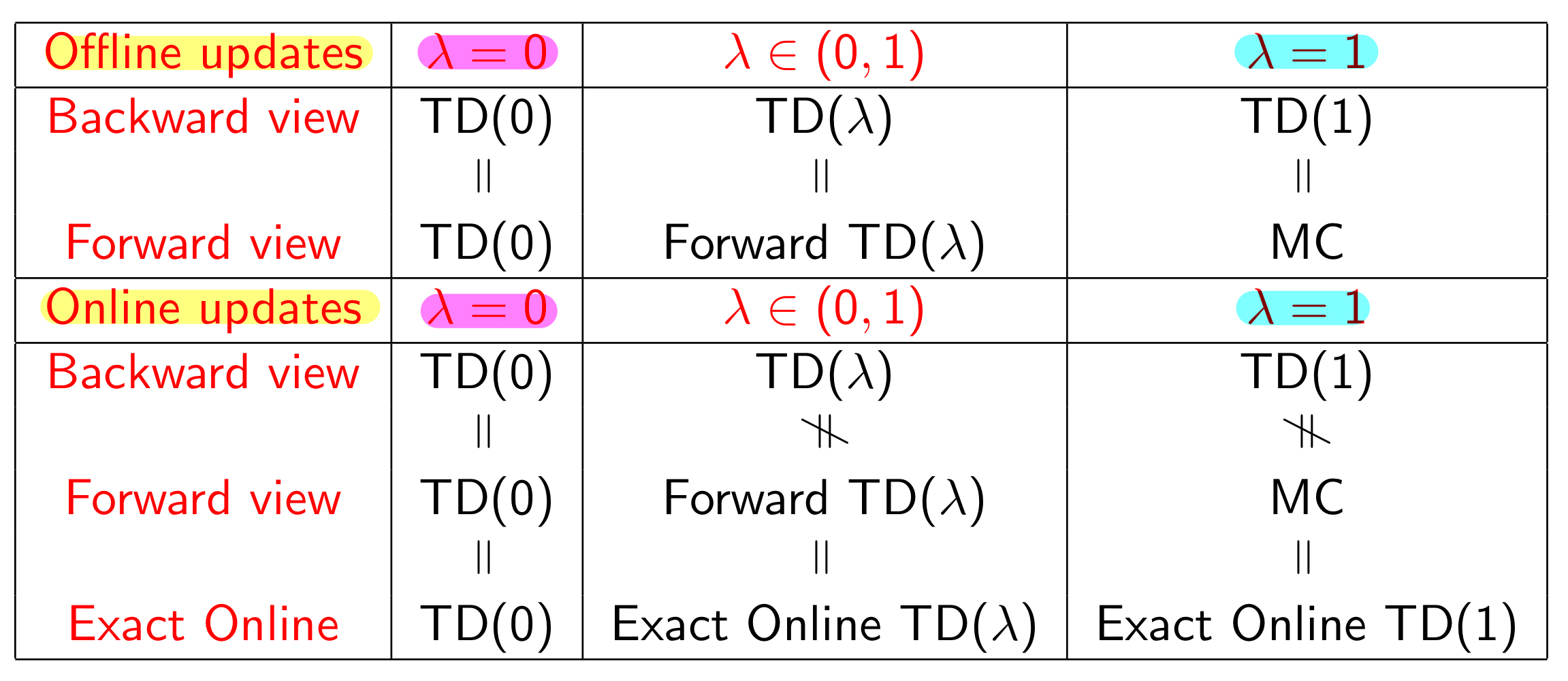
만약 $\lambda=0$(TD(0))이라면, Eligibility Trace에서 이전에 발생한 사건들에 대한 decay 없이, 가장 최근에 발생한 1 step 전의 state에 대해서만 update될 것이다. 이 경우, 처음에 봤던 TD(0)의 해석과 동일하다.

한편, $\lambda=1$(TD(1))이라면, Decay 없이 Episode의 처음부터 끝까지 모든 state에 동일한 update를 진행하게 된다. 이 경우 실시간 online update가 아니라 offline update 형태로 진행되고, TD(1)에서 발생하는 모든 update 값은 Monte Carlo에서 발생하는 모든 update의 합과 동일해지게 된다.

Summary

요약하면, Model Free Prediction 방법은 크게 Monte Carlo와 Time Difference가 있는데, 각각의 장단점을 잘 조합하고자 등장한 방법이 TD($\lambda$)이고, 그 안에서도 두가지 방법으로 문제를 해석하고 해결할 수 있다.