1줄 요약
Big O 표기법과 시간복잡도가 무엇인지 배우는 글
알고리즘을 풀고 싶은데 자료구조를 먼저 공부해야할거 같다. 지난번에 Linked List에 이어서 Big O 표기법, 시간복잡도를 배워보기로 했다. 시간복잡도는 한국어로하든 영어로하든 딱 들었을 때 너무 추상적이고 어렵게 들린다.
단어에서 풍기는 분위기로 배우는 게 아니라 이게 무엇인지 정확하게 이해하기 위해서 하나하나 짚고 넘어가는 동영상을 발견! 오늘은 이걸보면서 공부해봤다.
참고
https://youtu.be/D6xkbGLQesk ~15분까지
그 두가지 개념을 이해하기 전에 다음과 같은 의사코드(Pseudo-code)가 있다고 가정해보자.
given_array = [1, 4, 3, ..., 10]; // (1)
def find_sum(given_array); // ------- (2)
total = 0; // --------------- (3)
for each i in given_array; // (4)
total += i; // ------ (5)
return total; // ------------ (6)(1) - 길이가 정해져있는 배열 give_array
(2) - given_array를 파라미터로 가지는 find_sum함수를 정의
(3) - total을 0으로 초기화
(4) - given_array에 있는 요소들을 하나씩 꺼냄
(5) - 꺼낸 요소를 total에 더함
(6) - total을 리턴
이 함수를 보면서 자신에게 이런 질문을 할 수 있다.
이 함수를 실행하는 데에 시간이 얼마나 걸리는가?
이 질문은 답변하기 힘든 많은 요인이있다.
이 코드를 실행하는 컴퓨터가 얼마나 빠른지, 다른 프로그램을 같이 실행하고 있는지, 어떤 언어를 쓰는지 등 변수가 많기 때문이다.
그래서 이 질문을을 직접적으로 하는 대신에 관련있고 더 쉬운 질문을 할 수 있다.
이 함수의 런타임은 어떻게 증가하나?
- 런타임: time it takes to execute a piece of code
이 질문은 꽤 타당한 질문이다.
왜냐? 얼마나 많은 요소들이 배열에 있냐에 따라서 다른 총 양의 시간이 걸리기 때문이다.
즉, 더 많은 요소들이 있을수록 더 많은 요소들을 더해야 하기 때문이다.
수정된 질문으로 Big O Notation 과 Time complexity라는 한 쌍의 툴을 사용할 수 있다
이 툴을 사용하기 전에 실제로 이 함수가 얼마나 걸리는지 테스를 해보면 어떤 결과가 나올까?
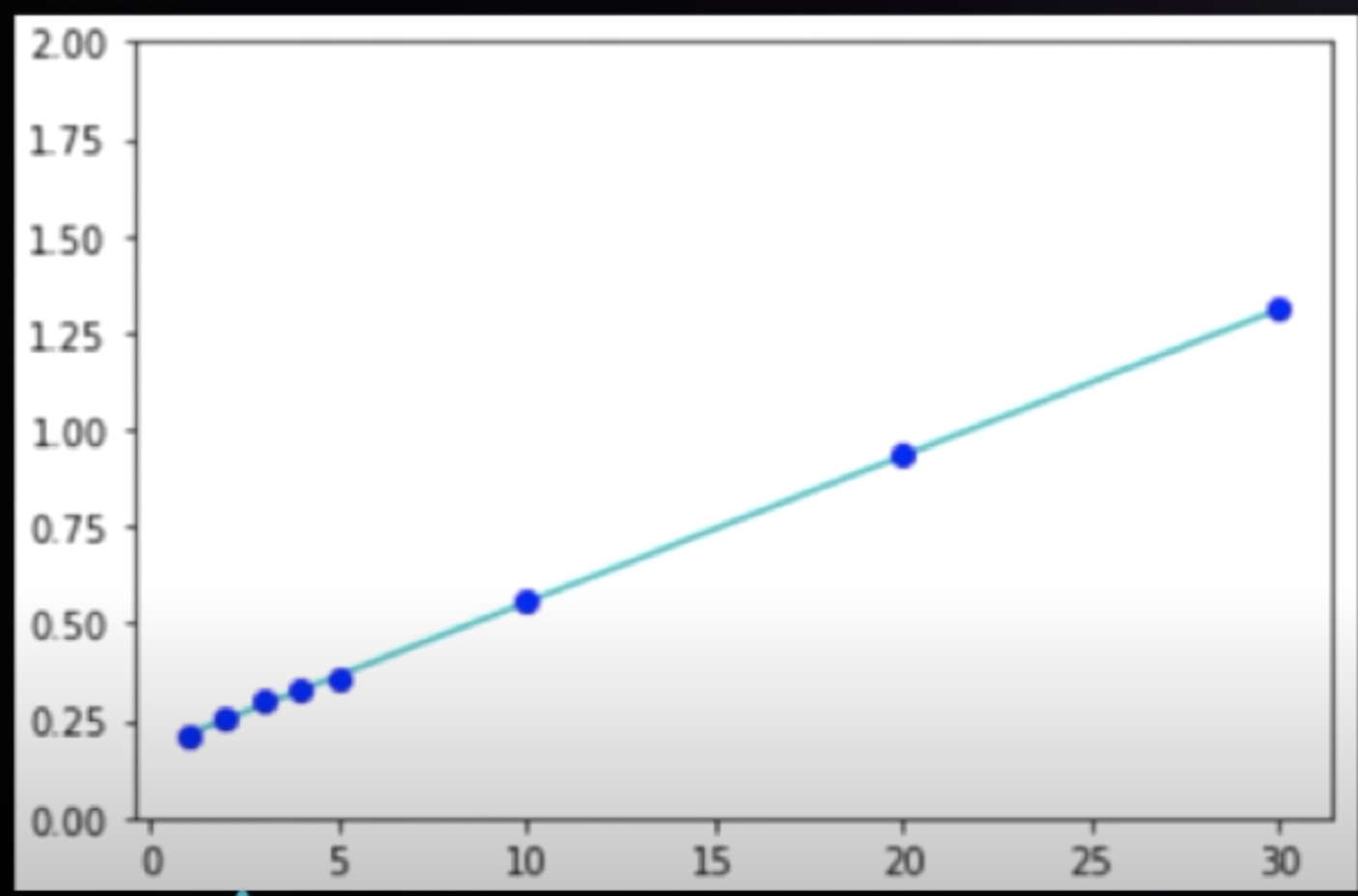
이 그래프는 요소들를 몇개를 넣었냐에 따라서(x축) 시간(y축)이 얼마나 걸리는지 보여준다. (참고로 시간은 microsecond)
이걸 보면 거의 일직선 형태로 증가하는 것을 볼수있다.
여기서 시간 복잡도를 Linear time (선형 시간)이라고 한다.
데이터의 양이 증가함에 따라 시간도 균등하게 증가하는 시간 복잡도이다.
시간 복잡도는 어떤 하나의 방법이다. 인풋이 증가하는 크기에따라 어떻게 한 함수의 런타임이 증가하는지를 보여주는 방법이다.
Linear time 외에도 다른 시간복잡도들이 있다.
Constant time
Quadratic time
이런 용어들을 좀 더 시스템적으로 부르는 용어가 있느냐?
그게 바로 Big O 표기법이다.
예를 들어서,
linear time은 O(n) 라는 Big O 표기법을 가지고 big oh of n 혹은 oh of n 이라고 읽는다.
n은 보통 인풋의 사이즈를 말한다.
이 경우에서는 give_array의 요소들의 개수이다.
constant time → O(1) -> big oh of one
quadratic time → O(n^2) → big oh of n square
그럼 이런 용어들이 Big O Notation으로 O(n)인지 O(1)인지 어떻게 아는거냐?
예를 들어,
linear time 의 함수의 그래프를 식으로 나타내면 (위에 있는 이미지)
T(시간) = an + b 라는 공식을 가질 것이다.
n은 요소들의 갯수이고 a와 b는 상수이다.
여기서 이게 어떻게 O(n)인지 알수있느냐?
간단한 트릭이 있다.
- find the fatest growing term
- take out the coefficient(계수)
T = an + b
여기서는 term이 2개가 있다.
an과 b!
여기서 가장 빠르게 증가하는 term은?
an!
a가 계수이므로 그걸 빼면 n만 남고
남은것이 괄호안에 들어가야한다.
그래서 O(n)이라는 것을 알수있다.
참고: 강의에 따르면 수학적으로 가장 legal한 방법은 아니지만 practical하게 사용할수있는 방법이라고 한다.
다른 예를 보자.
T = cn^2 = dn + e
- find the fastes growing term → cn^2 와 dn을 비교해보면 인풋이 늘어나면 늘어날수록 결국엔 cn^2가 가장 빠르게 증가하는 term이라는 것을 알수있다.
- take out the coefficient → n^2 → O(n^2)
Time complexity와 Big O Notation의 편리한 점은 함수에 대한 입력이 점점 커짐에 따라 함수가 확장되는 방식에 대한 개략적인 아이디어를 준다
또 다른 편리한점은 특정한 환경에 의존하지 않는다.
예를들어서 위에서 예시로 들었던 것을 새로운 맥북프로와 이때까지 사용하던 옛날 맥북프로로 실행했다고 치자.
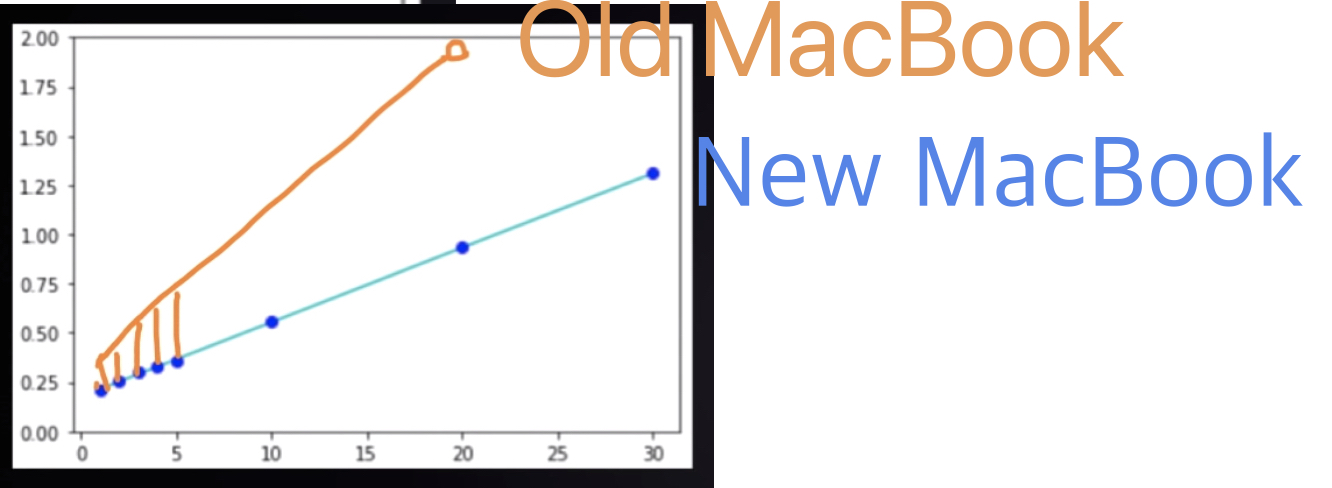
그럼 성능차이로 저런 그래프가 그려질건데,
식으로 나타내면 여전히 두개는 똑같이
T = an + b 가 된다.
이 말은 같은 Tme Complexity와 Big O Notation을 가진다는 말이다.
이번엔 O(1)을 이해하기 위해서 다음과 같은 의사코드가 있다고 치자.
given_array = [1,4,3...10]
def stupid_function(given_array);
total = 0;
return total;이전과 같은 실험을 했다고 생각해보자
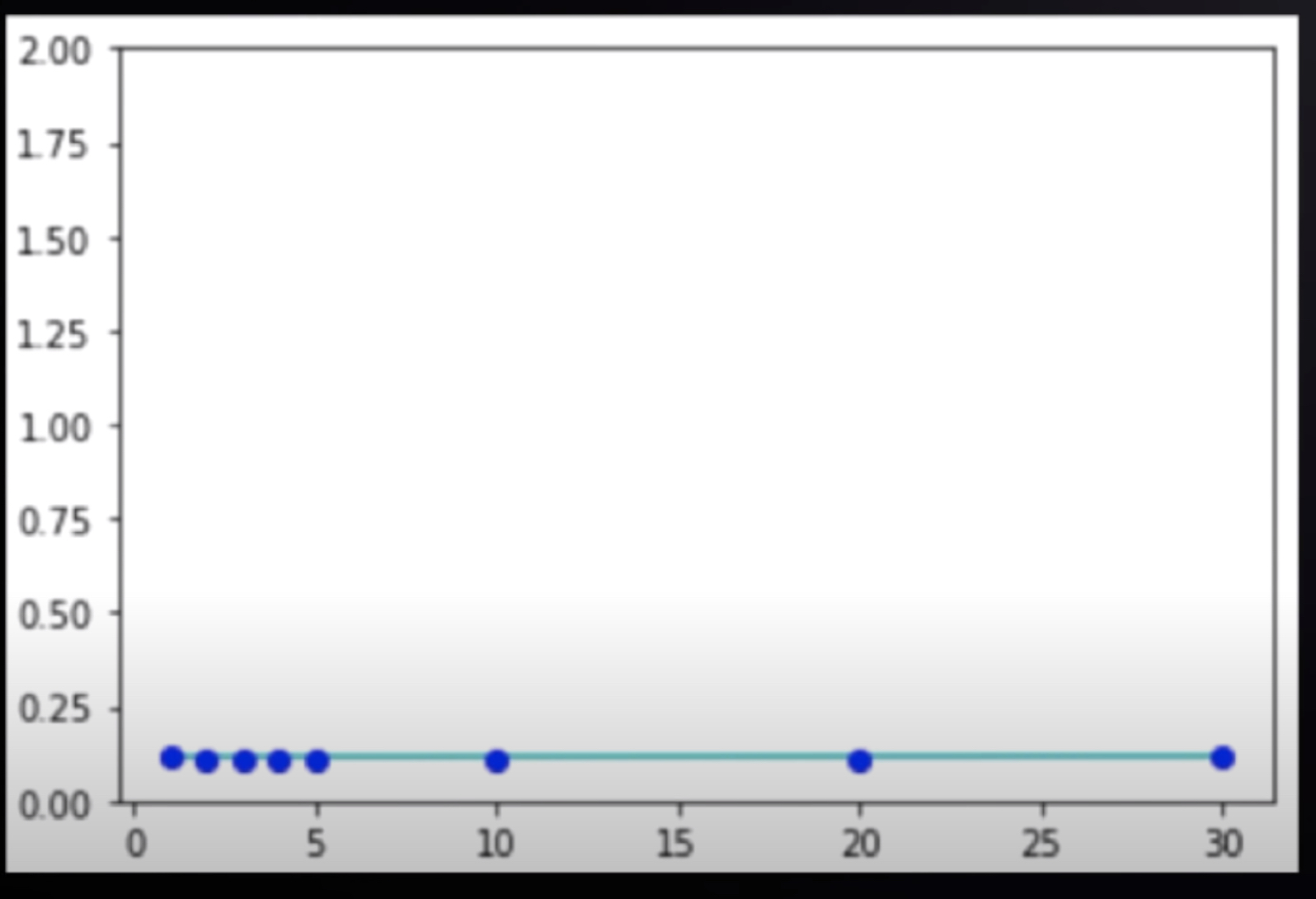
given_array로 아무것도 안하니까 이런 그래프가 나온다.
T = 상수 c 라고 식을 정해보자.
여기서 c = 0 .115 이라고 생각해보자.
Big(O)로 하려면 아까 진행했던 방식.
- fatest ...
- take out ...
...이 알고싶으면 복습차원에서 다시 올라가 확인
오직 0.115만 있으니까 가장 빠른 term이다
계수는 없다.
그래서 다음과 같은 방식이 적용이된다.
0.115 X 1
O(0.115)
O(1)
여기서 괄호안에 사실 상수는 아무거나 넣을수있다.O(2), O(3) 전부 가능하다.
O(1)을 사용하는 것은 컨벤션이 O(1)이기 때문이다.
이것을 Constant time이라고 부른다. 물론 시간이 constant이기 때문!