[자료구조] Tree - 트리

일상 회고록·2024년 7월 13일

tree 자료구조 트리

자료구조 모음집

목록 보기

6/7

안녕하세요~!

오늘의 주제는 Tree 자료구조입니다!

아마 Heap까지는 많이 들어보시고, 사용해보셨을텐데 Tree부터 조금씩 헷갈리는 개념이 나온다고 생각합니다 (뇌피셜)

그래서 최대한 꼼꼼하게 정리해보려고 합니다😛

저에게도, 다른분들에게도 많은 도움이 되었으면 합니다🍀

그럼 시작하겠습니다!

1. 개념

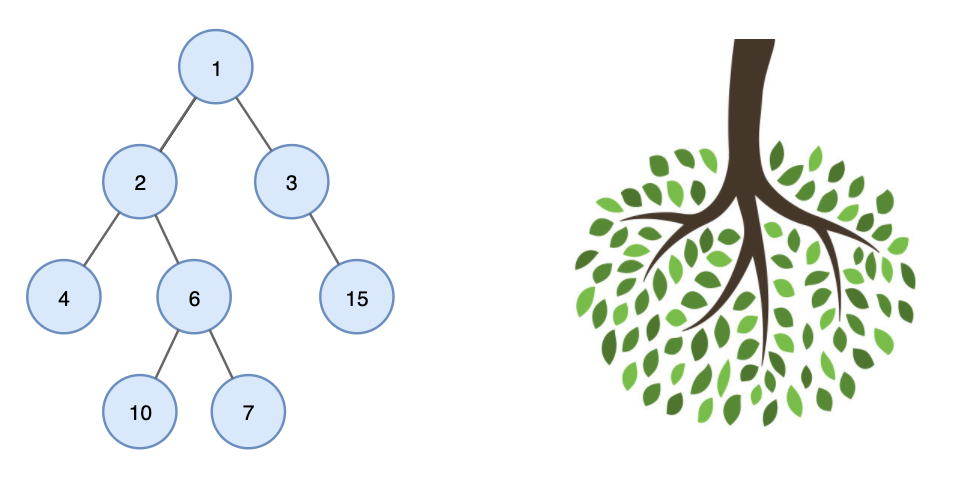
Tree - 트리는 그래프(Graph)의 한 형태로, 계층적인 관계를 표현하는 비선형 자료구조입니다.

값을 가진 노드끼리 연결되어 있는 구조가 아래로 계속해서 확장되는 구조를 가지고 있습니다.

실제 트리는 나무를 뒤집어 놓은 것 같은 모양으로 생겨 이름도 Tree가 되었습니다.

Graph - 여러개의 노드와 간선으로 이루어진 자료구조

저는 처음 트리 자료구조를 보았을 때 컴퓨터 상에서 어떻게 값을 저렇게 저장할 수 있지? 라는 의문이 있었습니다.

핵심은 한 노드에 값과 다른 노드와의 연결 상태를 함께 저장하는 것입니다 (포인터와 유사합니다)

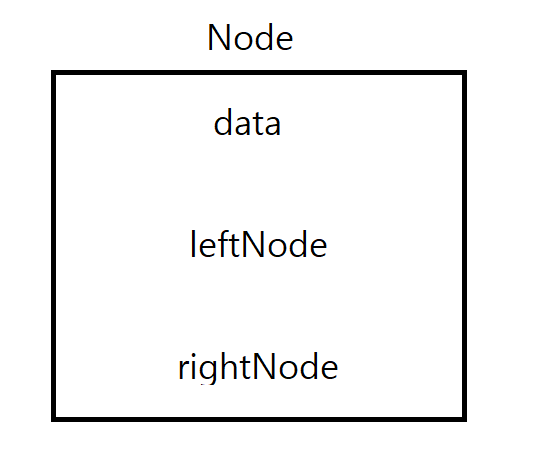
위와 같이 하나의 노드의 3가지 정보가 담기게 되는 것이죠!

트리 구조는 대표적으로 파일 시스템에서 디텍토리 구조에서 사용되고 있습니다.

(한번 쯤 직박구리 폴더안에 뻐꾸기 폴더 안에 앵무새 폴더 안에..)

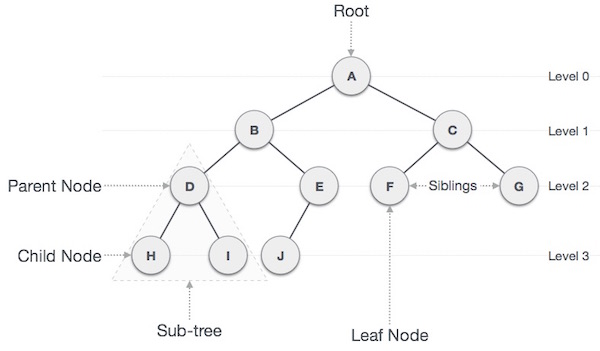
1-1. 구성 요소

노드 (Node) - 트리를 구성하는 한 요소을 의미
- 루트 노드 (Root) - 트리 상 최상위 노드
- 부모 노드 (Parent) - 자식 노드를 가진 노드
- 자식 노드 (Child) - 부모 노드의 하위 노드
- 형제 노드 (Sibling) - 같은 부모를 가지는 노드
- 단말 노드 (Leaf) - 자식 노드가 없는 노드
- 가지 노드 (Branch) - 자식 노드를 하나 이상 가진 노드
간선 (Edge) - 노드와 노드간의 연결 선을 의미
깊이 (Depth or Level) - 루트 노드부터 특정 노드까지의 간선 수
높이 (Height) - 특정 노드에서 리프 노드까지 경로 중 가장 큰 간선 수
차수 (Degree) - 노드가 가진 자식 수를 의미
넓이 (Width) - 동일 깊이에서의 노드 수
Order - 부모노드가 가질 수 있는 최대 자식 노드의 수 (이진트리는 Order가 2)

요소가 굉장히 많네요????

실제로 트리를 설명하며 자주 등장하는 용어들이니 꼭 한번 예시를 보면서 꼼꼼하게 보시길 추천드립니다. ~~(저처럼 어버버하지 마시길,,)~~

1-2. 특징

특징을 살펴볼까요?

트리믐 다음과 같은 특징들을 가지고 있습니다.

하나의 루트 노드와 0개 이상의 하위 트리로 구성
비선형 자료구조
트리 내에 또다른 트리가 있는 재귀적 자료구조
순환 구조를 가지지 않고, 무방향 그래프입니다.
부모 / 자식 관계가 있는 계층형 구조이며 모든 자식은 하나의 부모 노드만을 갖습니다.
노드가 N개라면 N-1개의 간선을 가집니다.

사실 특징이기도 하지만 트리이기 위한 규칙이기도 합니다.

해당 특징들로 인해 조금 특별한 그래프가 되는 것이죠.

따라서 위의 특징을 만족하지 못한다면 ‘트리’라고 할 수 없습니다.

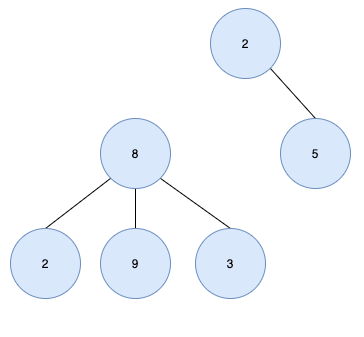
위 트리 구조는 루트 노드가 2개이므로 트리가 아닙니다.

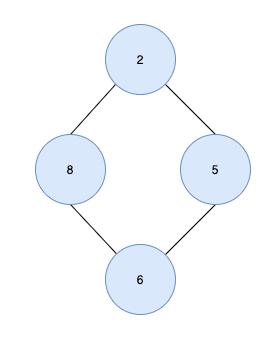
위 구조도 순환 구조를 이루기 때문에 트리라고 할 수 없습니다.

그렇다면 트리 종류에는 어떤 것들이 있을까요?

1-3. 종류

편향 트리 (Skew Tree)

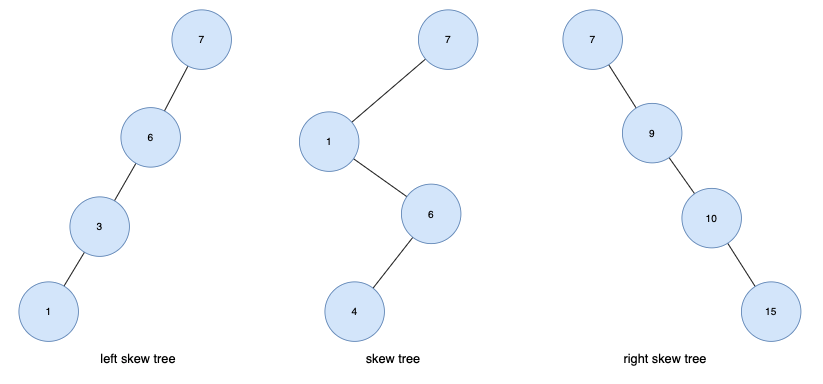
편향 트리는 모든 노드들이 하나의 자식 노드만을 가지는 트리 구조입니다

만약 왼쪽 방향으로만 자식을 가진다면 왼쪽 편향 트리, 오른쪽 방향으로만 자식을 가진다면 오른쪽 편향 트리라고도 합니다.

이진 트리 (Binary Tree)

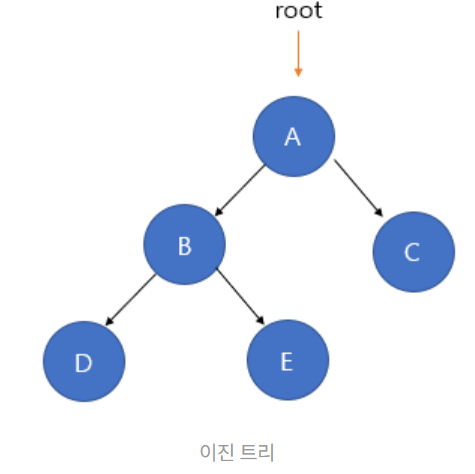
아마 제일 대중적으로 사용되는 트리 구조일거라고 생각합니다.

모든 부모 노드가 2개 이하의 자식 노드를 가지는 경우 이진 트리입니다.

2개 이하요??? 그렇다면 편향 트리도 이진 트리인가요???

맞습니다. 편향 트리도 이진 트리 중 하나라고 할 수 있습니다.

이진 탐색 트리 (Binary Search Tree)

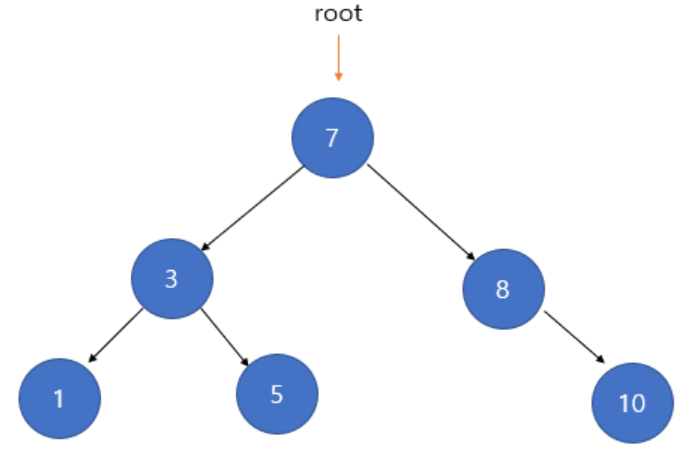
이진 탐색 트리는 이진 트리에서 노드의 값들이 정렬된 트리입니다.

일반적으로 부모 노드 값을 기준으로 왼쪽 노드가 작은 값, 오른쪽 노드가 큰 값을 가집니다.

다원 탐색 트리 (Multiway Search Tree)

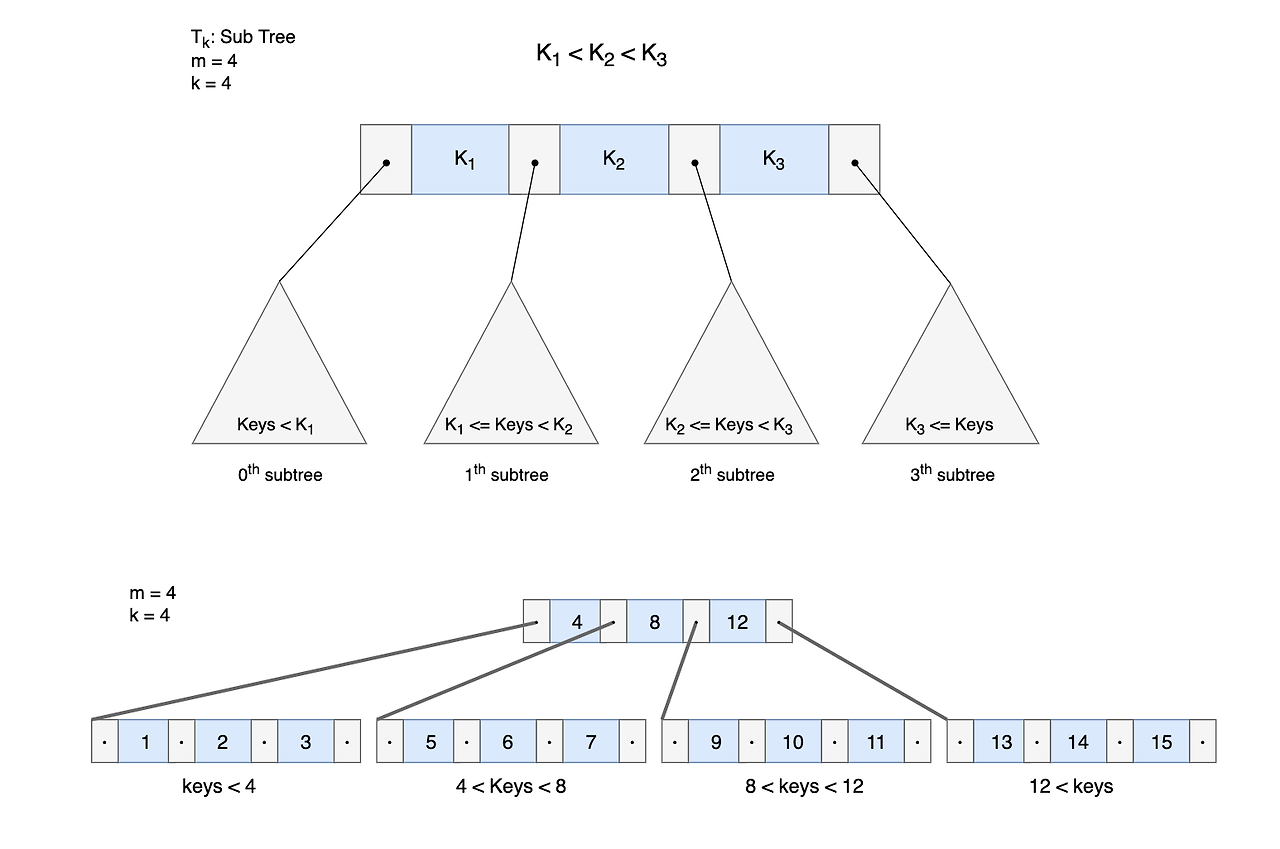
다원 탐색 트리는 한 노드안에 최대 m-1 개의 요소와 m개의 자식을 가질 수 있습니다.

(참고로 이진 탐색 트리는 m=2인 경우입니다)

즉, 서브트리를 최대 m개 가질 수 있고, 노드 안의 요소는 오름차순 정렬되어 있습니다.

다원 탐색 트리는 많은 요소를 저장함과 동시에 낮은 높이를 유지할 수 있다는 장점이 있습니다.

균형 트리 (Balanced Tree, B-Tree)

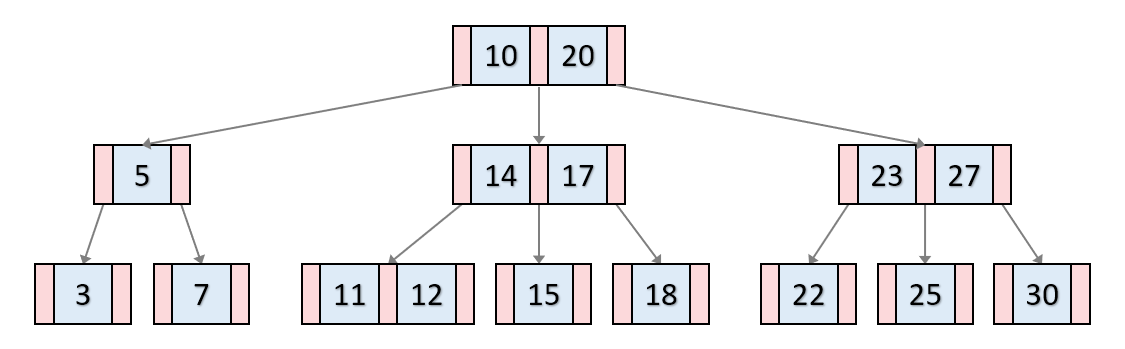
다원 탐색 트리는 스스로 높이 균형을 유지하지 못합니다.

이러한 단점을 보완하여 스스로 균형을 유지하는 트리 구조가 균형 트리입니다.

보통 B-Tree 라고 불립니다.

B-Tree는 따로 다룰 예정이라 이정도로 넘어가겠습니다

2. 순회 방식

트리의 순회 (Tree Traversal)은 중요한 주제입니다.

면접에서도 많이 나오는 질문이고, 탐색 알고리즘에도 많이 쓰입니다.

헷갈리는 경우가 많기 때문에 정확하게 알아야합니다.

트리 순회는 트리의 모든 노드를 한 번씩 방문하는 것을 말합니다.

순회 방식에는 3가지가 있습니다.

전위 순회
중위 순회
후위 순회

하나씩 살펴보겠습니다.

2-1. 전위 순회 (Preorder)

전위 순회는 부모 노드 (루트 노드) → 왼쪽 서브 트리 → 오른쪽 서브 트리 순으로 탐색합니다.

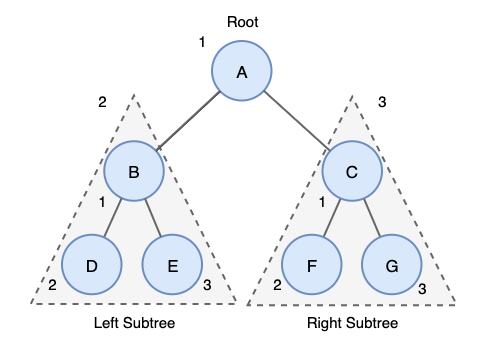
해당 예시에서 탐색 순서는 A → B → D → E → C → F → G 입니다.

2-2. 중위 순회 (Inorder)

중위 순회는 왼쪽 서브 트리 → 부모 노드 (루트 노드) → 오른쪽 서브 트리 순으로 탐색합니다.

보통 이진 탐색 트리에서 오름차순 혹은 내림차순으로 값들을 가져올 때 사용합니다.

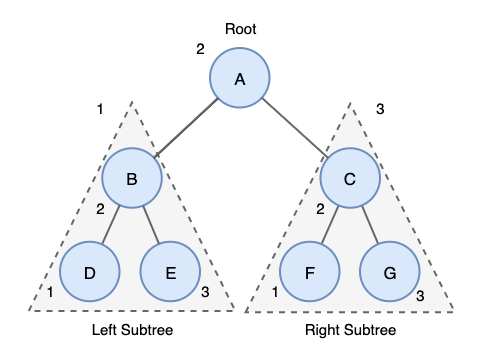
해당 예시에서 탐색 순서는 D → B → E → A → F → C → G 입니다.

2-3. 후위 순회 (Postorder)

후위 순회는 왼쪽 서브 트리 → 오른쪽 서브 트리 → 부모 노드 (루트 노드) 순으로 탐색합니다.

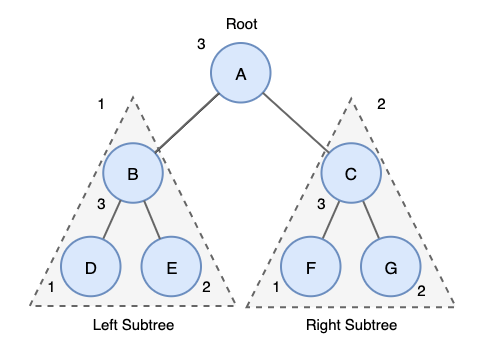
해당 예시에서 탐색 순서는 D → E → B → F → G → C → A입니다.

3. 구현

자바와 파이썬으로 트리를 사용해보도록 하겠습니다.

3-1. Java

자바에서 트리를 사용하기 위해선 직접 구현하거나 TreeMap, TreeSet을 사용해야 합니다.

TreeMap, TreeSet은 이진트리를 기반으로 구현되어 있기 때문에 추후 이진트리를 주제로 다룰 때 사용해 보도록 하고, 해당 포스팅에선 직접 구현해보겠습니다!

public class Tree {
		//노드의 수
    int count = 0;
    
    public class Node {
        Object data;
        Node left;
        Node right;

        public Node(Object data) {
            this.data = data;
            this.left = null;
            this.right = null;
        }

       public void addLeft(Node left) {
            this.left = left;
            count++;
       }

        public void addRight(Node right) {
            this.right = right;
            count++;
        }

        public void deleteLeft() {
            this.left = null;
            count--;
        }

        public void deleteRight() {
            this.right = null;
            count--;
        }
        
        public Object getData() {
		        return this.data;
        }
    }

    public Node addNode(Object data) {
        Node n = new Node(data);
        return n;
    }
}

먼저 위와 같이 트리 클래스와 노드 클래스를 생성해줍니다.

//트리 생성
Tree tree = new Tree();

// 노드 생성
Node root = tree.addNode(1);
Node left = tree.addNode(2);
Node right = tree.addNode(3);
        
// 루트 노드에 자식 노드 추가
root.addLeft(left);
root.addRight(right);

Object value = root.left.getData() // 출력 -> 2

위와 같이 트리구조를 생성하고, 루트 노드와 자식 노드도 생성하여 설정해주었습니다.

참 쉽죠?

3-2. Python

파이썬도 비슷한 방식으로 구현하면 쉽게 트리 구조를 사용할 수 있습니다.

class Node:
    
def __init__ (self, data=None):
		self.data = data
		self.left = None
    self.right = None

# 전위 순회
def preorder (node): 
    if node:
	    print(node.data, end=' ')
      preorder(node.left)
      preorder(node.right)

root = Node('A') 
r_left = Node('B')
r_right = Node('C')

root.left = r_left
root.right = r_right