안녕하세요~!
오늘의 주제는 직전에 다루었던 트리에 이어서 이진트리에 대해 좀 더 자세히 알아보도록 하겠습니다!
이진트리 자체는 생소하지 않지만, 그 안에서 생각보다 종류가 많습니다🤮🤮🤮
꼼꼼하게 정리해보도록 하겠습니다.
그럼 시작하겠습니다!
1. 개념
Binary Tree - 이진트리는 이름에 걸맞게 모든 노드들이 2개 이하의 자식을 가진 트리 형태를 의미합니다.
이진트리에 종류가 많은 이유도 딱 2개를 갖는 것이 아닌 2개 이하만 충족하면 되기 때문에 그렇습니다.
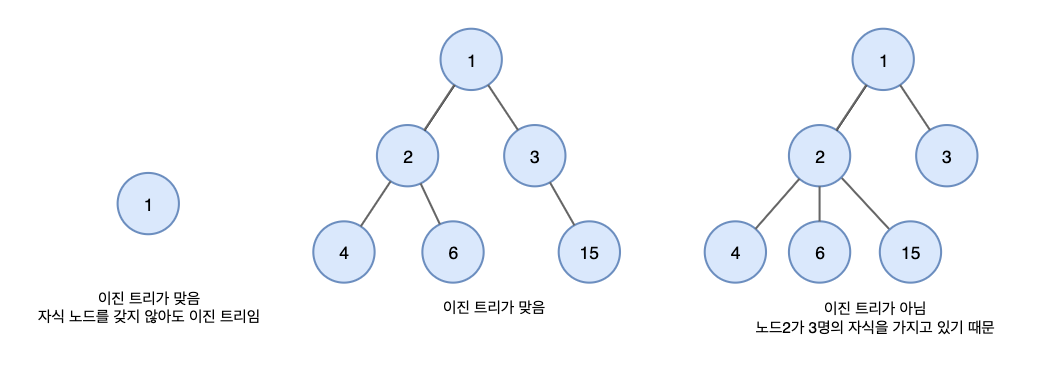
위와 같이 루트 노드만 덜렁 있어도 이진트리입니다. (머쓱~)
이진트리의 네임드들에 대해서 하나씩 살펴보겠습니다.
1-1. 종류
정이진트리 (Full Binary Tree)
루트 노드를 포함한 모든 노드가 0개 혹은 2개의 자식만을 가지는 트리 형태입니다.
위와 같이 왼쪽은 노드 중 하나가 1개의 자식만을 가지기 때문에 정이진트리가 아닙니다.(이진트리는 맞습니다)
반면 오른쪽은 모든 노드가 0개 혹은 2개의 자식만을 가지기 때문에 정이진트리입니다.
완전 이진트리(Complete Binary Tree)
정이진트리가 있지만, 완전 이진트리도 있습니다.
완전 이진트리는 마지막 레벨, 즉 가장 아래 단을 제외한 모든 레벨이 완전히 채워져 있는 형태의 트리입니다.
또한 마지막 레벨은 모두 채워져 있지 않아도 되지만 노드는 왼쪽 → 오른쪽 순서로 배치되어야 합니다.
완전히 채워져 있다는 의미는 해당 레벨에서 가질 수 있는 최대 노드의 수를 만족한다는 의미입니다.
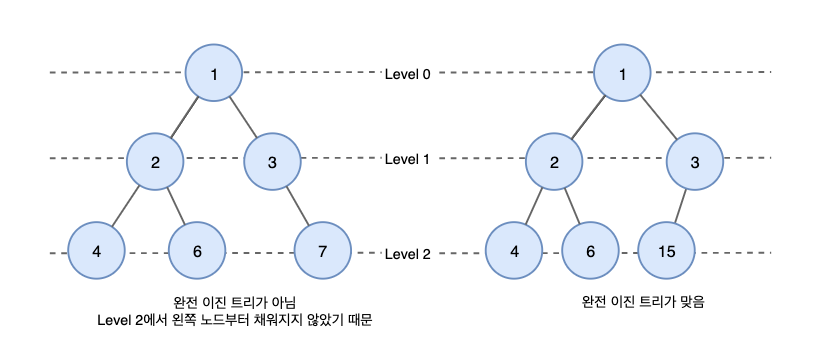
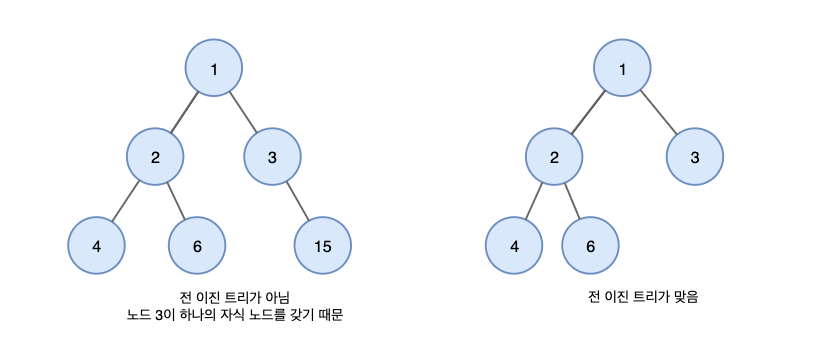
위처럼 왼쪽의 경우 마지막 레벨을 제외한 모든 레벨은 완전히 채워져 있지만, 마지막 레벨의 배치 순서가 맞지 않습니다. (왼쪽보다 오른쪽이 먼저)
반면 오른쪽은 모든 조건을 만족하기 때문에 완전 이진트리입니다.
정리해보자면, 완전 이진트리는 아래의 조건을 만족하면 됩니다.
-
마지막을 제외한 모든 레벨은 완전히 채워져 있습니다.
-
마지막 레벨은 왼쪽 → 오른쪽 순서로 노드가 배치됩니다.
포화 이진트리 (Perfect Binary Tree)
full, complete, perfect 다 나오네요 ㅎㅎ
포화 이진트리는 정이진트리이면서 완전이진트리인 형태의 트리입니다.
-
모든 리프 노드가 동일한 레벨을 가집니다
-
모든 레벨이 완전히 채워져 있습니다. (모든 노드가 두개의 자식 노드를 가집니다)
위의 조건을 만족하면 포화 이진트리입니다.
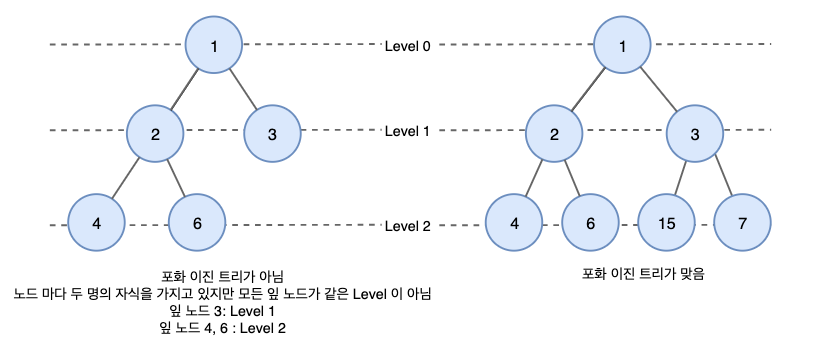
위처럼 왼쪽은 리프 노드가 동일 레벨에 있지 않기 때문에 포화 이진트리가 아닙니다.
(그렇다면 정이진트리일까요? 완전 이진트리일까요?)
반면 오른쪽은 모든 레벨이 완전히 채워져 있고, 모든 리프 노드가 동일한 레벨에 있어 포화 이진트리입니다.
편향 이진트리 (Skewed Binary Tree)
동일한 높이의 이진 트리가 여러개 있을 경우 최소의 노드 개수를 가지는 형태의 트리입니다.
동시에 자식 노드들이 왼쪽 혹은 오른쪽으로만 연결되어 있습니다.
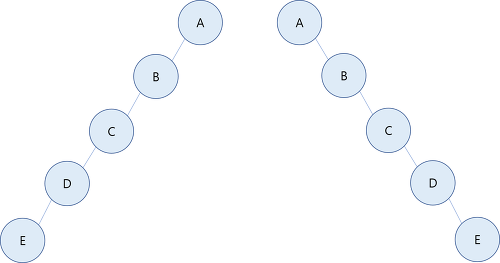
참고로 편향이진트리는 동일 방향으로만 연결되어 있기 때문에 Linked List 와 동일한 성능을 가집니다. O(n)
균형 이진트리 (Balanced Binary Tree)
왼쪽과 오른쪽 트리(서브 트리)의 높이 차이가 모두 1이하만큼 나는 트리 형태입니다.
조금 특이한 조건을 만족해야합니다.
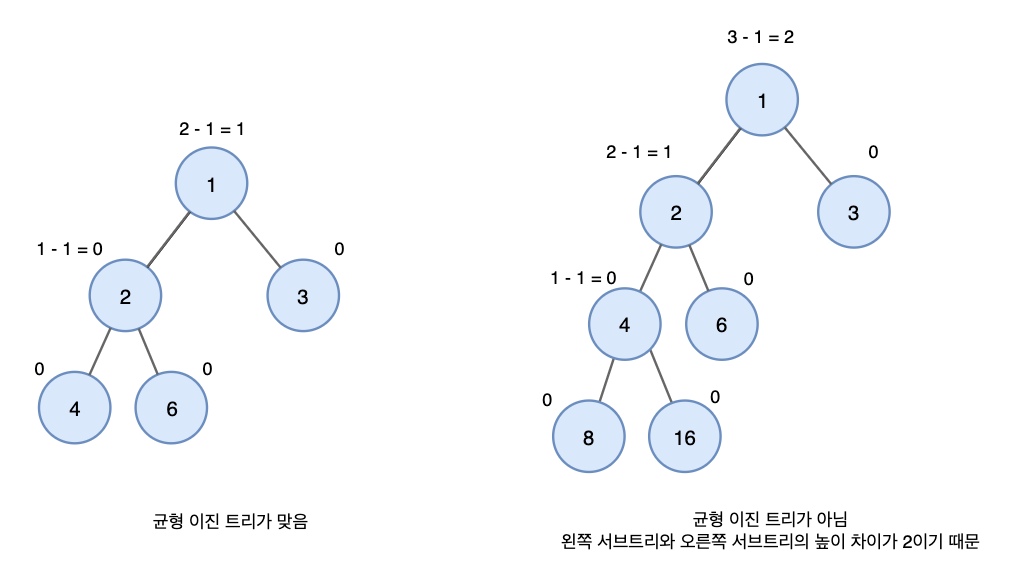
위와같이 왼쪽의 경우 모든 노드의 높이 차이가 1 이하이기 때문에 균형 이진트리입니다.
반면 오른쪽은 루트 노드의 높이 차이가 2이기 때문에 균형 이진트리가 아닙니다.
한 번씩 손으로 그려가며 파악해보시면 더 이해가 잘 될거거겁걱겁니다!
높이 균형 이진 탐색 트리 (Adelson-Velsky and Landis, ALV 트리)
통칭 AVL트리는 스스로 균형을 이진 탐색 트리 종류 중 하나입니다.
Balance Factor 를 통해 왼쪽과 오른쪽의 높이 차이가 절댓값 1 이하를 유지합니다.
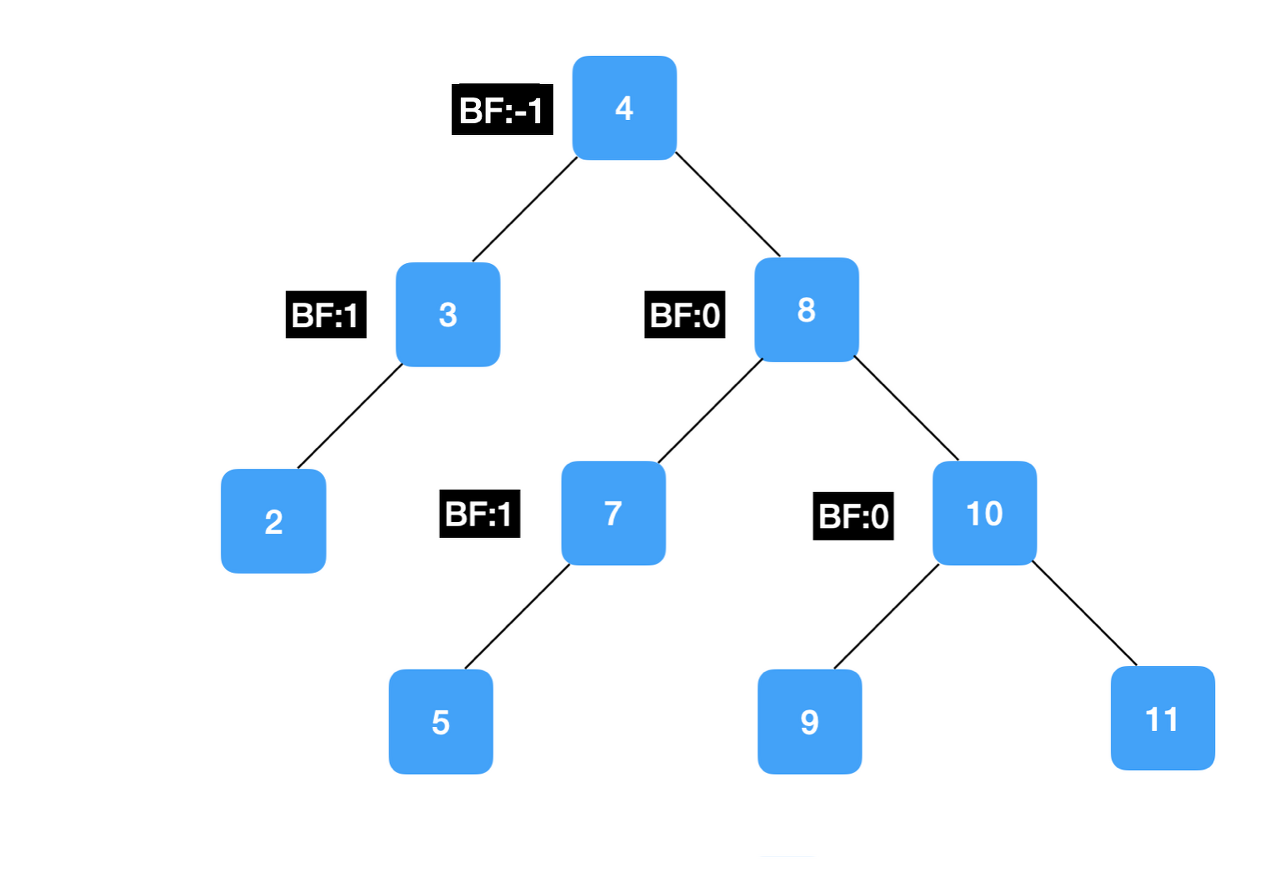
균형을 유지하는 세가지 방법은 레드-블랙 트리 시간에 자세히 다루도록 하겠습니다.
레드-블랙 트리 (Red-Black Tree)
레드-블랙 트리는 자가 균형 이진 탐색 트리로서 AVL트리처럼 스스로 균형을 유지합니다.
특이한 점은 이름처럼 노드마다 색깔을 가지고 있습니다.
레드-블랙 트리가 균형을 유지하는 방식은 따로 다룰 예정이기 때문에 이정도로 설명하고 넘어가겠습니다 😊

이번 포스팅은 트리의 연장선인 이진트리의 여러 종류에 대해서 알아보았습니다!
아직 트리 관련 포스팅이 Red-Black Tree와 B-Tree(B+-Tree) 가 남아있습니다.
TMI로 자바의 TreeMap과 TreeSet 을 현 포스팅에서 다룰까 했는데, 레드-블랙 트리 개념을 알고 다루는 것이 좋다고 생각되어 미루었습니다,,ㅎㅎ
그래서 비교적 간단하게 마무리하였습니다
오늘도 읽어주셔서 감사합니다~!🍀🍀🍀
References
