1. 1부터 n까지의 합
a. 루프를 활용한 방법

b. 재귀적으로 작성
def sum(n):
if n==1: return 1
return sum(n-1) + n- n까지의 합은 n-1까지의 합에 n을 더한 것과 같다.
c. 수행시간
- 루프를 활용한 경우 매번 상수번의 기본 연산만 수행했으므로 O(n)
- 재귀함수의 경우 T(n) = T(n-1) + 1, T(1) = 1
d. 점화식 T(n) = T(n-1) + 1, T(1) = 1 풀기
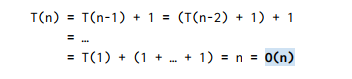
2. 1부터 n까지의 합. (다르게 계산)
a. 먼저 a부터 b까지의 합을 구하자.
b. sum(a,b) 는 a부터 b까지 더한 값을 리턴한다.
c. a와 b의 중간값을 m라 하자. (m = (a+b) // 2)
d. sum(a, b) = sum(a,m) + sum(m+1,b) 로 재귀호출한다.
- 두 번의 재귀호출이 이루어진다.
- a == b인 경우에 a를 리턴한다.
e.
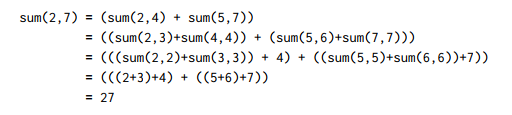
f. 코드를 보자.
def sum(a,b):
if a==b:
return a
m = (a+b) // 2
return sum(a, m) + sum(m+1, b)
g. sum(1, n) 을 호출한다. 점화식은 다음과 같다.
-
T(n) = T(n/2) + T(n/2) + c = 2T(n/2) + c, T(1) = 1
-
전개하자.
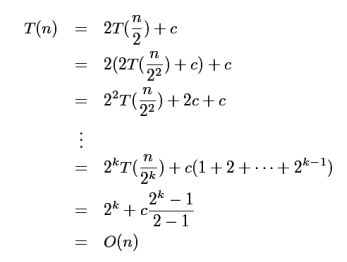
3. factorial 계산
팩토리얼 계산을 재귀로 구현해보자.
def factorial(n):
if n == 1: return n
else: return n * factorial(n-1)이를 이용하여 List A 에 있는 가장 큰 수를 찾는 재귀함수 find_max(A, n) 을 작성해보자.
def find_max(A,n):
if n == 1: return A[0]
return max(find_max(A[:n-1], n-1), A[-1])n까지의 가장 큰 수는 n-1까지와 n번째 수 중 큰 것이겠지? 그것을 구현한 코드이다. 나머지는 신경쓰지 말자.
4. 리스트의 값 거꾸로
a. A값을 반대방향으로 재배치하는 함수 reverse(A) 를 재귀적으로 작성해보자.
b. Sol1) 이 방법의 경우 재귀적으로 n만큼 호출한다.
def reverse(A):
if len(A) == 1:
return A
return reverse(A[1:]) + A[0] c. Sol2) n//2 만큼만 재귀적으로 호출하면 된다.
def reverse(A, start, stop):
if start < stop-1:
A[start], A[stop-1] = A[stop-1], A[start]
reverse(A, start+1, stop-1) e. 점화식을 계산해보자.
- 첫 번째 방법
T(n) = T(n-1) + c, T(1) = 1
n의 일을 다음 진행할 때 n-1 만큼으로 줄였기 때문에 다음과 같이 작성.
만약 slicing 을 포함하는 시간이라면
T(n) = T(n-1) + cn 이라고 작성해도 좋다.
- 두 번째 방법
T(n) = T(n-2) + c , T(1) = 1
n의 일을 다음번 호출할 때 2개를 버리고 n-2 만큼의 일로 줄였기 때문.
5. {0, 1, ... , n-1} 집합의 모든 부분집합
a. 부분집합의 개수가 2^n 개이므로 그 이상의 수행 시간이 필요하다.
시간복잡도는 O(n* 2^n) 이다! 이해만 하고 넘어가자.
def gen_subsets(k):
if k == n:
print(S)
else:
S.append(k)
gen_subsets(k+1)
S.pop()
gen_subsets(k+1)
S = []
n = int(input())
gen_subsets(0) 6. 길이가 n인 모든 순열
a. 순열의 개수가 n! 이므로 당연히 그 이상의 시간이 필요.
def gen_permutation():
if len(P) == n:
print(P)
else:
for i in range(1, n+1):
if chosen[i] == True:
continue
chosen[i] = True
P.append(i)
gen_permutation()
chosen[i] = False
P.pop()
P = []
n = int(input())
chosen = [False for _ in range(n+1)]
gen_permutation() 반복문을 돌려 모든 수에 대해 들어갔는지 체크, 들어갔다면 그냥 지나감.
들어가지 않았다면 체크해주고, 넣는다. > 재귀 > 체크 해제하고 빼주는 과정을 반복.