p.58 하노이 탑 : 분할정복 문제
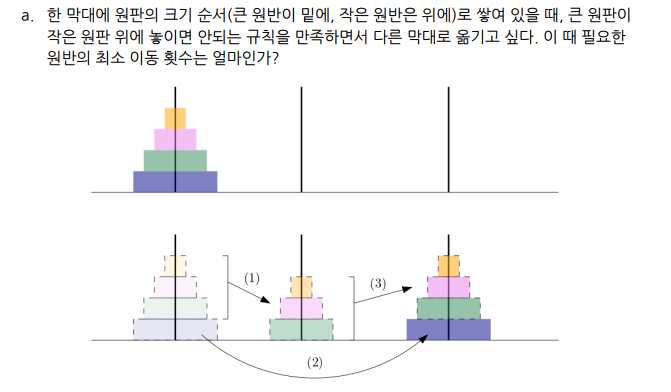
A,B,C (기둥)과 n개의 원판이 이 주어진 경우.
1. 위부터 n-1개를 B로 옮긴다. : A(n-1) > B
2. 가장 큰 것을 C로 옮긴다. : n > C
3. B의 n-1개를 C로 옮긴다. : B(n-1) > C
2번은 1번의 연산이며, 1,3 번은 재귀연산이다.
따라서 T(n) = 2T(n-1) + 1 ( T(1) = 1 ) 과 같다.
이를 전개하여 빅오로 나타내면 다음과 같다.
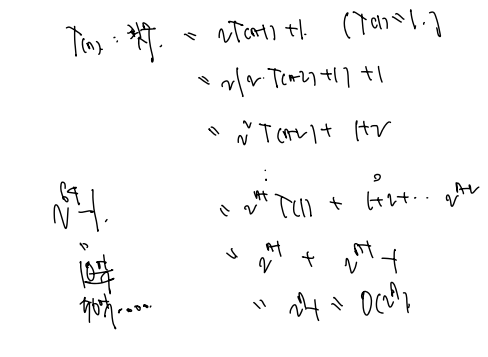
O(2^n) 의 시간이 걸린다. n = 64개의 원판이라면 50억번의 연산이 필요하다..
p.59 이진탐색 (Binary Search)
이진탐색이란 쉽게 말해 원하는 값을 반으로 갈라 찾는 것이다. (한번의 비교로 범위를 반으로 줄인다!)

g. Slicing + 재귀 (bad)
슬라이싱과 재귀를 이용한 이진 탐색이 있다.

풀 때마다 범위가 줄어드는 O(logN) 이며 슬라이싱 복사시간이 n(1 + 1/2 + 1/2^2 + ... ) = 2n 이다. 따라서 O(n) 이다.
h. Slicing X + 재귀

재귀로 호출하는 것은 같은데 굳이 슬라이싱 해서 넣는 것이 아니라 매개변수를 이용하여 중앙값을 인자로 받는 것이다. 매개변수는 (전체 리스트, 탐색시작, 끝, 목표값) 으로 하여 목표값이 중앙보다 아래 있으면 l부터 m-1 까지 탐색, 위에 있으면 m+1부터 r까지 탐색하는 것으로 한다.
이 경우 슬라이싱이 없고 풀 때마다 범위가 반씩 줄어듦으로 O(logN) 이다.
i. slicing X + 비재귀
가장 바람직한 이진탐색 코드이다.

시작할 때는 l을 0, r을 -1인 인덱스로 잡고 K의 위치에 따라 시작값 또는 끝값을 조정하는 방식이다. 반복문 안에서, K가 중간 아래면 끝값 = 중앙 - 1 로 업데이트, 중간 위면 시작위치 = 중앙 + 1 로 업데이트하면 된다. 이 경우는 깔끔한 O(logN) 이다!
p.64 봉우리 찾기 (peak finding)
리스트 A에 봉우리가 있다면 봉우리를 하나 출력하는 문제.

- 최대값이 존재한다면 무조건 봉우리가 존재한다고 할 수 있다.
- A[0] 부터 봉우리인지 n번 검사할 수 있다.
- 그보다 이진탐색이 가능하다.
A[k-1] > A[k] 이라면, A[0] 과 A[k-1] 사이에 무조건 하나 이상의 봉우리가 존재한다. (왼쪽으로 커진다면 끝에도 있을 수 있고, 작아진다면 k-1 이 봉우리다. - 따라서 T(n) = T(n/2) + c 이고, T(n) = O(n) 이다.
2차원 ver.
동서남북 이웃보다 커야 봉우리라고 정의한 문제를 풀자.

방법은 다음과 같다.
- m/2 열에 대해 최대값을 찾는다. (해당 A[i][m/2] 는 그 열에서 최대값이다.)
- 그러면 A[i][m/2-1] 또는 A[i][m/2+1] 과의 비교를 통해 봉우리를 바로 찾거나 m/2 열의 왼/오른쪽에 있음을 안다.
- 만약 오른쪽이 더 크면 계속해서 오른쪽의 수보다 더 큰 수를 쫓아갈 수 있다.
- 그러나 m/2 열을 지나칠 수는 없다.
이 과정을 반복하면
T(n) = n + n + T(n/2)
T(n) = T(n/2) + cn = O(n) 임을 알 수 있다.
p.64 연속된 정수 합이 최대가 되는 구간
n개의 정수가 저장된 리스트 A를 가지고, 연속된 정수들의 합이 최대가 되는 구간을 찾아보자.
몇 가지 방식을 알아보자.
-
만들 수 있는 총 구간의 개수는 n^2, 구간의 합은 O(n)의 연산이 필요하므로 O(n^3)
-
p: prefix sum 을 정의한다. p란 순서대로 해당 p[i] 까지의 합을 계산한 것이며, 이러한 p를 정의하는데는 O(n)이 소요된다. 그렇다면 모든 쌍 (i,j)에 대해 특정 구간의 합을 p[j] - p[i-1] 이라고 정의할 수 있으며 가능한 쌍의 조합은 n^2이다.
따로 처리하는 것이므로 O(n) + O(n^2) + C = O(n^2)
- 분할정복 방법으로 O(nlogn)으로 해결한다. 다음과 같은 리스트에서 최대 구간이 존재하는 경우는 오직 3가지 뿐이다.

- L에 있는 경우, R에 있는 경우, 걸쳐 있는 경우
- L또는 R에 있는 경우는 재귀적으로 구한다.
- 걸쳐 있는 경우는 L의 가장 끝부터 왼쪽으로 prefix 합을 구하면서 큰 구간을 찾고, R은 오른쪽으로 prefix 합을 구하면서 가장 큰 구간을 찾아 연결한다. 두 번의 prefix 합을 계산하는 것이기에 O(n) 이면 충분.
- max(L,R,M)

따라서 T(n) = 2T(n/2) + cn = O(nlogn) 이다.
이는 전개해서 알 수도 그림으로 알수도 있다. 이번엔 그림으로 풀자.
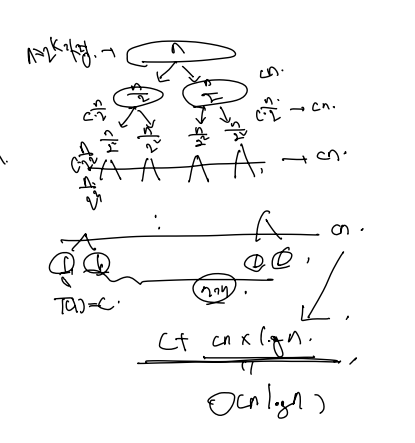
n = 2^k 라 가정하면 쭉쭉 내려가면서 최종적으론 1개까지 내려오며 (C) 각 단계에서 Cn 연산을 총 logn 단계 반복하므로 nlogn 이 된다.
T(n) = T(n/2) + cn 이면?
궁금증을 확장하여, 하나의 문제를 반개짜리 2개가 아닌 반개짜리 하나 + cn 의 연산을 해보자.
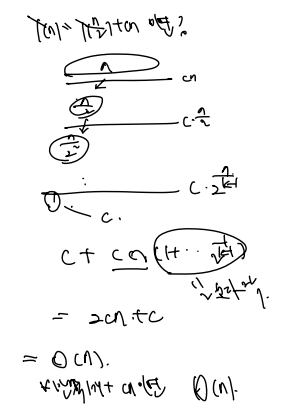
역시나 1까지 내려오기에 C , Cn(1 + 1/2 + ...) <= 2Cn 연산하기에 O(n)이다.
다시말해 하나짜리 문제를 반쪽 1개 + cn 에 풀면 O(n) 이다.
다른 식들은 어떨까?
- 하나의 식을 반쪽짜리 하나, 둘, 셋, 넷으로 쪼갠 시간복잡도를 한꺼번에 보자.

순서대로 n의 지수가 log2(2), (예외) , log2(3), log2(4) 가 된다.
그런데 하나의 문제를 반개짜리 3개로 나눠푸는 건 도대체 어떤 문제일까? 예시를 보자.
✅ 세자리수 곱
세자리수 세자리수는 다음과 같이 곱셈 9번과 덧셈 3 3 (곱할 때마다 한다고 하자.) + 3 * 6 (다 더하고 6자리 수 3개를 더한다.), 총 36번의 연산을 할 수 있다. 교과서 같은 계산방식에 따르면 O(n^2) 인 것.
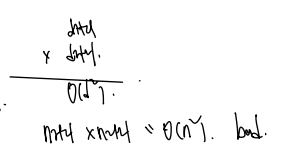
✅ karatsuba algorithm
새롭게 제시된 알고리즘에서는
n자리수 곱셈 문제 1개 = n/2 자리수 곱셈 문제 3개로 분할한다.
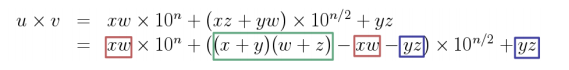
이는 xw, yz 연산의 경우 2T(n/2) 이며 (x + y)(w + z) 는 각각 n/2 + 1 이므로 T(n/2 + 1) 을 계산한 것이다. 따라서 간단히
T(n) = 3T(n/2) + cn 으로 계산해도 좋다.
Big-O 로의 전환과정은 다음과 같다.
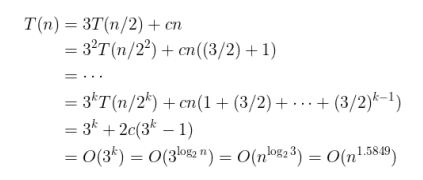
이를 멋있게 일반화할 수 있다.
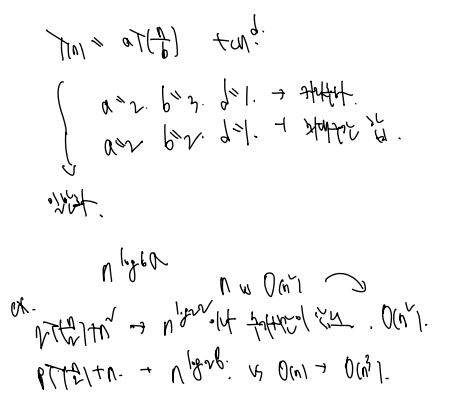
여기에 일반화된 앞의 식과 뒤의 식을 비교하여 (합으로 구성되어 있으므로) 큰 것을 선택하면 그것이 O 연산이 된다.
p.69 이차원 행렬곱
이차원 행렬 곱 역시 n(행 선택) n(열 선택) n(곱한 후 합) = O(n^3) 연산이지만 이는 학교 식을 게산한 것으로 더 줄일 가능성이 있다. : 분할정복으로 풀자.
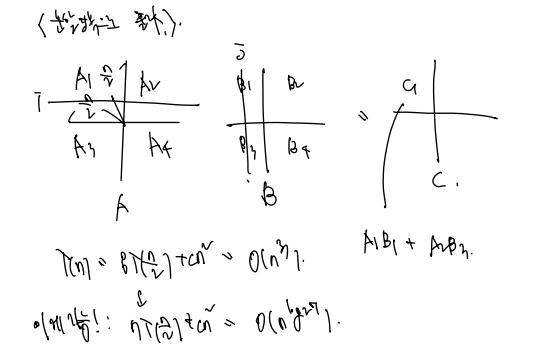
각각 반으로 갈라 푸는 8T(n/2) + cn^2 이 지배적이었는데, 이후 7으로도 풀 수 있음이 밝혀지며 시간을 줄였다.