1. Selection problem
선택 문제의 공통적인 구조를 알아보자.
a. 입력: 리스트에 n개의 수와 1과 n사이의 자연수 값 k가 주어진다.
b. 출력: 입력으로 주어지 수 중 k번째로 작은 수를 찾아 리턴한다.
c. 목표: 비교 횟수를 최소화하자
2. Problem 1: 최대값 찾기 (k = n)
a. 다음 코드를 보자.

시작 최대값은 A[0] 으로 설정하고, 반복문을 돌면서 현재 최대 < 새로 들어온 값이라면 현재 최대 = 새로들어온 값으로 할당하고 최대를 반환한다.
b. 비교횟수? > n-1
c. 이 외에도 토너먼트 방식으로 비교해서 찾을 수 있으나 이 경우에도 반드시 n-1 번의 비교가 필요하다
d. 하한 증명법에 따른 내용으로 n-1 보다 적게 비교해서 최대를 찾을 수가 없다.
3. Problem 2: 가장 작은 수와 가장 큰 수를 모두 찾기 (k=1, k=n)
a. 알고리즘 1
n-1 번의 비교로 가장 작은 수를 찾고, 가장 작은 수 1개를 제외한 n-2 번의 비교로 가장 큰 수를 찾을 수 있다. > 총 비교횟수 2n -3 번.
b. 알고리즘 2
-
n이 짝수라고 가정할 때, 가장 작은 수를 토너먼트로 찾으면 n-1 번의 비교로 찾을 수 있다. (1라운드 탈락 한 수 중 가장 큰 수가 존재한다!)
-
1라운드에서 탈락한 수는 n/2 개 또는 n/2+1 개이다.
-
탈락 한 수 중 가장 큰 값이 전체에서 가장 큰 값이다. 여기서의 비교는 n/2 -1 번.
-
따라서 전체 비교 횟수는 3n/2 - 2 번이면 된다.
-
하한 증명에 따라 이보다 작은 비교는 불가능!
4. Problem 3: 가장 작은 수와 두 번째로 작은 수 찾기 (k=1, k=2)
a. 토너먼트 비교를 이용해보자.
b. 가장 작은 수가 토너먼트 우승자라면, 두 번째로 가장 작은 수는 무조건 가장 작은 수를 만나 패배한 수이다.
c. 두 번째로 작은 수가 될 수들은 몇 개일까? 가장 작은 수가 대적했던 수들이므로 log2n의 올림한 값이다.
d. (n - 1) + (log2n - 1) 번의 비교로 가장 작은 두 수를 찾을 수 있다!
5. Problem 4: 임의의 k번째로 작은 수 찾기 (k는 입력으로 주어지는 일반적인 선택 문제)
a. k = 1 이면 최솟값, k = n 이면 최댓값, k = n/2 이면 중간 값 찾는 문제와 동일하다
b. n개의 수와 함께 k가 입력으로 주어진다.
c. 찾고 있는 수가 존재할 범위를 줄여나가자가 포인트.
d. 어떤 알고리즘의 경우 처음 n개에서 k 번째를 찾는 문제가 있다고 하자. > 추가 작업하여 범위를 반으로 줄임 > 다시 추가작업으로 반으로 줄임 > 반복 > 남은 하나가 찾는 값!
추가작업에 2n (그냥 제시된 수이니까 걱정말자.) 이 든다면 비교횟수는 다음과 같다.
T(n) = T(n/2) + 2n, T(1) = 1
이를 점화식으로 푸는 과정을 제대로! 보자.

T(n) <= 4n + 1 = O(n) 이 성립한다.
본격적으로 이러한 알고리즘을 하나하나 정복해나가면 된다.
✅ Quick Select 알고리즘
-
현재의 후보 중에서 임의의 수 하나를 선택한다. (pivot)
-
pivot 보다 작은 수는 S, 같은 수는 M, 큰 수는 L로 분류
- |S| > k 라면 >> S 에서 k 번째로 작은 수를 찾자.
- |S| + |M| < k 라면 >> : k 번쨰로 작은 수는 L 에 있다. L에서 k - |S| - |M| 번째로 작은 수를 찾으면 된다.
- 위의 두 경우가 아니라면 그수는 바로 피봇이므로 이를 리턴하면 된다.
def quick_select(A, k):
코드 🔽
def quick_select(A, k):
p = A[0]
S, M, L = [], [], []
for i in range(len(A)):
if A[i] < p: S.append(A[i])
elif A[i] > p: L.append(A[i])
else: M.append(A[i])
if len(S) > k: quick_select(S, k)
elif len(S) + len(M) < k: quick_select(L, k-len(S)-len(M))
else: print(p)
A = [1,3,6,4,2,7,8]
quick_select(A, 3)수행시간 🔽
Best case:
T(n) = T(n/2) + cn

Worst case:
T(n) = T(n-1) + cn

✅ MoM 알고리즘
- S와 L 의 크기를 1/4 이상, 1/4 이하가 되도록 하는 알고리즘
- 아이디어: Pivot 을 추가로 시간을 들여 선택하자.
-
A 의 수를 다섯 개씩 묶는다. (하나의 열을 구성, n/5 개의 열.)
-
각 열에 대해 다섯 수들의 중간값을 찾는다. (중간값보다 작은 < 중간값 < 중간값보다 큰 수로 배열)
-
n/5 개의 중간값들을 모두 모아 이 값들의 중간값을 찾는다. (알고리즘을 n/5 개에 대해 재귀호출) 해당 중간값을 m* 이라 한다.
-
열의 중간값이 m* 보다 작으면 왼쪽, 크면 오른쪽으로 모은다.
-
m* 을 기준으로 구역을 다음과 같이 나눈다.
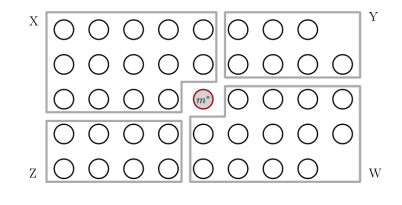
-
X의 값들은 확정적으로 m 보다 작고, W의 값들은 확정적으로 m 보다 큰 값이다. 다른 값들은 확정적이지 않다.
-
S = X + {Z, Y 중 m 보다 작은 값}
L = W + {Z, Y 중 m 보다 큰 값}
M = m* 와 같은 값. -
|S| > k 이면 S에 대해 재귀호출, |S| + |M| 이면 L에 대해 재귀호출, 둘 다 아니라면 m* 리턴
비교횟수, Big-O 계산 🔽
-
5개 중 중간값을 찾는 횟수는 몇 번? 넉넉히 10 번이라 하면 10 * (n/5) = 2n 번ㅇ로 중간값
-
중간값들의 중간값을 찾을 때 T(n/5) 번, 이제 m* 가 정해진다.
-
모든 값을 m* 와 비교할 때 n 번
-
8의 과정에서 재귀호추할 때 최악의 경우 T(3n/4) 번의 비교가 필요.
T(n) <= T(3n/4) + T(n/5) + 2n + n
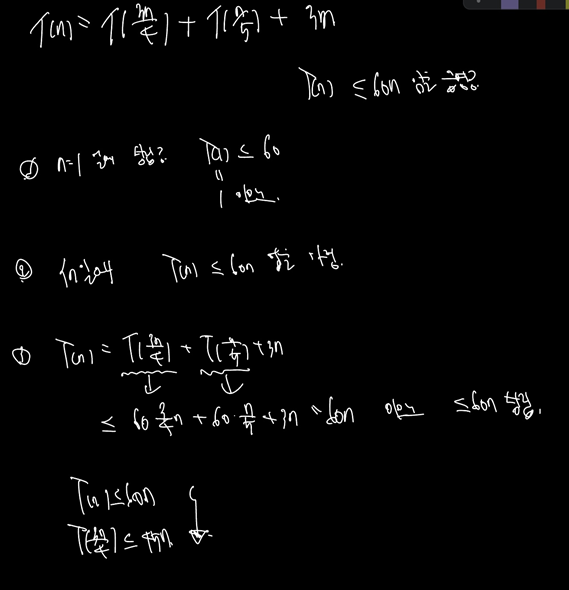
코드 🔽

각 빈칸은 각각
-
i = i + 5
-
?
-
medians, len(medians)/2
-
S.append(v)
-
L. append(v)
-
len(A) > k >> MoM(S, k)
-
len(A) + len(M) < k >> MoM(L, k-len(S)-len(M)