[HUFS/Algorithm] Huffman Code, 최소 못의 개수, Pinning, Backtrack, N-Queens

📚 목차

• Huffman Code 구현
• Pinning 문제 (1, 2, 3)
• Backtracking
• N-queens

🔨 Huffman Code 구현

그리디 알고리즘 중 허프만 코드 문제가 있었고,
1. Decode Tree 를 통해 prefix-free code 를 만족시키며
2. 비용 = 빈도수 X 비트 수 = f(x) X depth(x) 를 최소로 하기 위해 빈도수가 높으면 루트와 가깝게, 빈도수가 낮으면 루트와 멀어도 ok.
두 가지를 구현해보자.

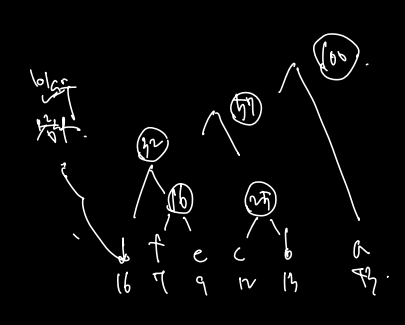
a-f 까지 6개의 알파벳 빈도수 f가 주어진다고 하자.
f = [7, 12, 5, 10, 4, 2] 이다.

코드는 다음과 같다.

H = [] 
for x in range(n): # O(nlogn) 
	heap.heappush(H, (f(x), str(x)) # H에 (빈도수, 인덱스) 형태로 넣기) 
while len(H) > 1: # n-1 >> O(nlogn)
	a = heapq.heapop(H) # 1 (빈도수, 문자), logn
    b = heapq.heapop(H) # 2 (빈도수, 문자), logn
    heapq.heappush(H, (a[0] + b[0], (a[1], b[1]))), logn
tree.string = heapq.heappop(H)[1] 

다음 코드를 실행시키면 빈도수가 낮은 것부터 하나씩 묶어 가장 높은 빈도수를 마지막에 묶을 수 있다.

허프만 코딩의 빅오는 앞서 코드에서 O(nlogn) + O(nlogn) + O(n) = O(nlogn) 이다. 이때 O(n) 은 만든 트리를 하나씩 탐색하며 뎁스를 확정하는 것이다.

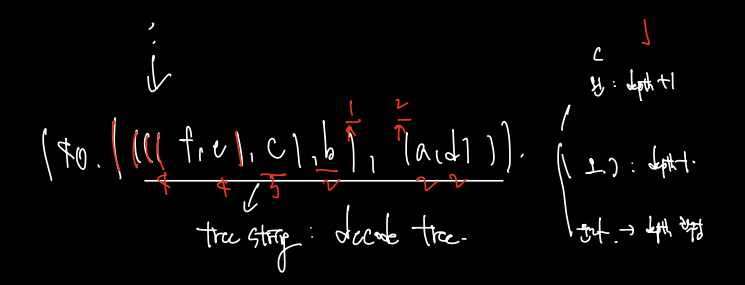
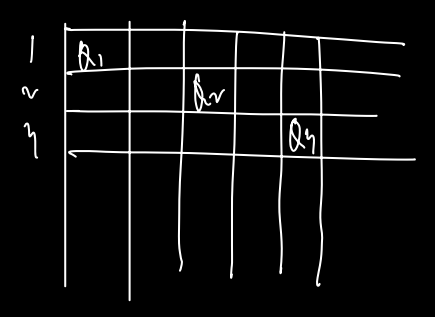
🔨 Pinning 문제 1, 2, 3

못의 개수와 막대 수로 만들 수 있는 문제들이다. 각각의 조건과 아이디어가 다르니 알아두자. 아이디어도 알아두고 구체적인 순서 하나하나까지를 숙지해두면 되겠다. 1, 2번은 Greedy 고 3번은 DP로 푸는 것 또한 염두에 두자.

문제 1🔽 (못 1 => 최대 막대 수?)

문제 1번은 못이 1개가 주어지고 막대들이 주어질 때 하나의 못으로 최대 몇 개의 막대를 꽂을 수 있을 지 반환하는 문제이다. (막대 개수의 최대 값 반환)

간단하므로 바로 순서로 넘어가자.
1. 막대의 왼쪽 끝, 오른쪽 끝을 하나의 배열에 모아 오름차순 정렬한다
2. 하나씩 보면서 왼쪽 끝이라면 꽂은 개수를 +1하여 기록, 오른쪽 끝이라면 꽂은 개수를 -1하여 기록한다.
3. 기록 중 max 를 반환한다

• 시간은 정렬과 O(nlogn) 선형 스캔 O(n) 이 + 으로 묶여 O(nlogn)

문제 2🔽 (n개 막대 => 최소 못의 수?)

이번엔 n개 막대가 주어질 때 모든 막대는 꽂히면서 못의 개수를 최소로 하려면 몇 개의 못이 필요한지 반환하는 문제.

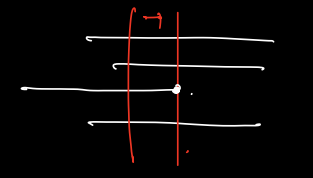
다음과 같이 아무데나 못을 찍는 것에서 ➡️ 오른쪽 끝점 묹로 변환한다.
이는 Continous 한 문제를 Discrete 하게 바꾸는 것을 의미하며, 이렇게 바꾼 후에는 Greedy 하게 문제를 풀면 된다. (강의실 배정 문제!)

순서를 보자.
1. 오른쪽 끝을 기준으로 가장 처음 끝나는 지점에 못을 박는다. (끝나는 지점에 하나를 박지 않으면 그 막대는 못이 없으므로 반드시 박아야 한다.)
2. 그 후 관통 막대 중 또다시 오른쪽 끝을 기준으로 처음 끝나는 지점에 못을 박는다
3. 반복

• 오른쪽 끝에 대한 정렬이 필요하므로 O(nlogn) 의 시간. 나머지는 선형 스캔.

따라서 강의실 최대 배정 문제와 최소 관통 못의 수는 같은 문제이다. (최대와 최소를 찾는 문제인데도 같다!)

문제 3🔽 (n개 막대, m개 못 => 관통 가능 최대 막대 수?)

이번에는 상황을 바꾸어 막대 수n과 못의 수m이 모두 주어졌을 때 관통하는 최대 막대 수를 구하는 문제를 생각해보자. (모든 막대를 무조건 통과하는 게 아니니까!) (최대 구간 막대 개수를 반환한다.)

결과적으로 이 문제는 Greedy 가 아니다. DP문제임!
1. 이 문제 역시 오른쪽 끝 점 기준으로 오름차순 정렬하는 과정이 필요하다. O(nlogn)
2. DP[k][j] 를 오른쪽 끝 점 j에 k번째 못을 박았을 때, k개의 못으로 꽂을 수 있는 막대의 최대 개수라 하자.
3. k개의 못으로 꽂을 수 있는 막대는 k-1개로 꽂은 막대 + 새롭게 k번째 못만이 꽂는 막대의 수가 될 것이다. 따라서 k-1못이 놓여있는 오른쪽 끝 점은 i라 하자. k번째 못만이 꽂는 막대의 수는 m(i, j) 로 주자.
DP[k][j] = max(DP[k-1][i] + m(i, j) (i < j)
DP테이블까지 끝! 각 과정에 따라 시간복잡도를 보자.

1. 오른쪽 끝 기준 정렬이 필요하다. (DP[k][j] 의 j가 오른쪽 끝 j이므로): O(nlogn)
2. DP[1][j]를 먼저 다 채워야 한다. 못 한개로 j번째 끝에 몇 개를 꽂을 수 있을지는 1번 문제에서 선형 스캔과 같다. (n개 못이므로) O(n)
3. DP[k][j]를 본격적으로 채운다. 한 칸을 채울 때 t의 시간이 걸린다고 하면(기본적으로 m(i,j)계산이 O(n)) m, n 까지 채워야 하므로 O(mnt) 의 시간이 걸린다.
4. 마지막으로는 정의에 따라 max(DP[m][1] DP[m][2] ... DP[m][n]) 을 반환을 한다. 왜냐? m개의 못을 다 쓰는 건 맞지만 마지막 꽂는 지점이 n이 될 수도, n-1 이 될수도.. 모르기 때문이다. (뭐 그런데 하나의 못은 당연히 하나의 막대는 꽂을 것이니 DP[m][m] 부터 DP[m][n] 사이에 답이 있을 것이다.)

Backtracking

사실 Divide&Conquer, DP, Greedy 문제는 어렵지 않은 문제에 속한다. 왜? 다항시간 안에 해결하기 때문!

그럼 어려운 문제란 무엇일까? 아마 지수시간에서야 해결될 수 있는 문제일 것이다. 예컨대 집합 {8, 6, 7, 5, 3, 10, 9} 라는 집합이 주어질 때 합이 S = 15 가 되는 부분집합이 있는지(Yes) 없는지(No) 출력하는 문제(Subset problem)가 있다고 하자.

이러한 문제의 경우 정답은 {8, 7}, {5, 10}, {6, 9}, {3, 5, 7} 로 Yes 가 당연해보이지만 사실 합이 잘 만들어지지 않는 경우에 판별이 어렵다. 모든 Subset 을 먼저 계산해보아야 하고 O(2^n) 각각의 경우에 합의 계산까지 해야 하므로 O(n) 총 시간복잡도는 O(2^n * n) 이다.

모든 경우를 이렇게 다 계산할 수 밖에 없을까? 지수시간 알고리즘 중에서도 빠른 알고리즘은 없을까? 그게 바로 Backtracking 이다!
모든 경우를 다 해보되, 일단 가보고 아니면 back하여 되돌아오는 방법을 사용한다.

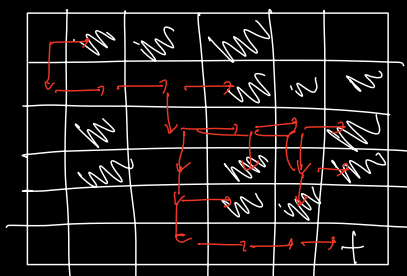
다음과 같이 미로가 있다고 했을 때

• 일단 동으로 가보고
• 막히면 돌아오고
• 남으로 가보는 알고리즘을 설계하면 된다.
  

🔨 N-queens 문제

같은 행, 열, 퀸이 위치한 대각에 다른 퀸을 놓을 수 없을 때 가능한 조합의 수를 출력하는 문제이다. 다음과 같이 4 X 4 칸이 주어질 때 가능한 경우의 수는 2이다.

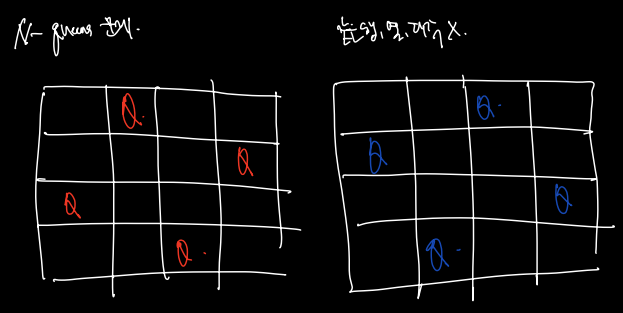
이 경우 n X n 의 board 크기가 주어지고, 퀸의 수 또한 n이므로, 경우의 수는 n^n이다.

이제 N-queens 문제를 Backtracking 으로 풀어보자.

정답 배열을 x라하면 각 행에 어떤 열에 퀸을 채울지 배열에 숫자를 넣을 수 있다. 4 X 4 의 경우 정답은 x = [2,4,1,3], [3,1,4,2] 이다.

다음은 수도 코드.

x = [] # 정답을 저장할 배열 
def Nqueens(k):
	if k > N: # n+1 의 경우 n X n 을 이미 넘었다는 뜻으로 다 채움. 출력 
    	print(x)
        return 
    else: # 그렇지 않을 경우 채우는 중. k번째 퀸 모두 try 
    	for c in range(1, N+1): 
        	if B(k, c) == True: # k-1 까지 모두 충돌 체크, 들어갈 수 있다면 
            	x[k] = c # k 행에 c열에 배치한다고 기록 
                Nquuens(k+1) # k+1 행으로 넘어감 
                
def B(k, c): # 퀸이 k행의 c열에 들어갈 수 있는지 검사 
	for i in range(1, k): # 1행부터 k-1 행을 돌며 
    	if x[i] == c or |i-k| == |x[i]-c|: # c 같은 열에 이미 있는지, 또는 (i, x[i]) 와 (k, c) 의 비교이므로 행의 차 = 열의 차인지(대각) 확인
        	return False
    return True

약간 헷갈리는 부분은 if x[i] == c or |i-k| == |x[i]-c| 이 부분이나 비교하는 부분이 i, x[i] 와 k, c이고
1. 같은 열에 이미 있거나 x[i] == c
2. 대각에 있으면 i+x[i] = k+c 이므로 이에 대한 차를 절댓값으로 표현

둘 중에 하나라도 만족하면 False 를 출력하면 된다.