목차
💡 Greedy Algorithm
🔨 강의실 배정
🔨 사다리타기
🔨 Huffman Code
Greedy Algorithm (욕심쟁이 알고리즘)
➡️ 객관적, 단순한 전략으로
➡️ 알고리즘 정확성에 대한 증명이 필요
1원, 5원, 10원, 100원이 주어지고
689원을 개수 최소로 지불하는 방법을 고민해보자.
= 100 X 6 + 10 X 8 + 5 X 1 + 1 X 4 => 총 19개의 동전을 지불해야 한다.
이게 정말 최소일까? 왜? (최소임을 증명해야 한다.)
- 1, 5, 10, 1000이 배수 관계에 있으므로 높은 단위로 낼 수 있다면 그렇게 하는 것이 유리하기 때문이다.
- 귀류법으로 증명할 수도 있다. 19개가 최소동전이 아니라, 다른 방법이 있다고 가정하는 것! 상대의 주장을 나의 주장 선택으로 하나씩 바꿔가며 이 가정이 거짓이라는 것을 밝히면, 증명이 됨을 이용하는 방법이다.
🔨 강의실 배정 문제
하나의 강의실이 있고 수업 시간이 (시작시간, 종료시간) 이 주어질 때, 수업들을 겹치지 않게 선택할 수 있는 최대 강의 수를 결정하는 문제.
수업 시간은 다음과 같이 주어진다고 하자.
(1, 5) -1
(2, 7) -2
(2, 4) -3
(6, 9) -4
(1, 10) -5
(4, 8) -6
(6, 11) -7
(3, 7) -8
아래의 그림과 같이 나타내자.
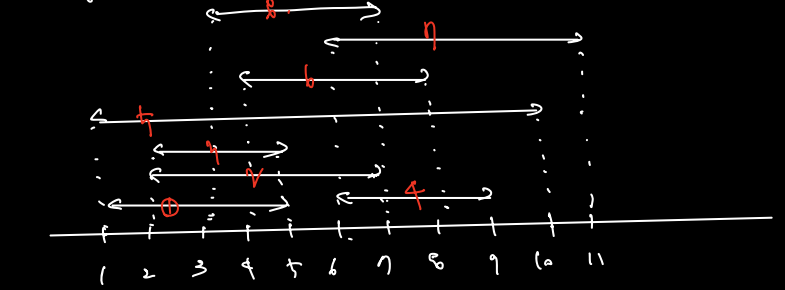
- 강의 시간이 짧은 강의부터 배정
- 3부터 배정하게 된다.
- 반례
- 일찍 시작하는 강의부터 배정
- 반례

- 겹치는 강의를 각각 계산하고, 적게 겹치는 강의 먼저 배정
- 반례
- 붉은 색 먼저 배정되지만 (겹치는 강의 4개, 2개, 4개)
- 푸른 색 조합이 낫다
- 일찍 끝나는 강의 먼저 배정 ⬅️ 답 (= 뒤에 남는 시간이 많은 강의)
다음과 같은 상황에서의 Greedy 정답을 보고 이를 귀류법으로 증명
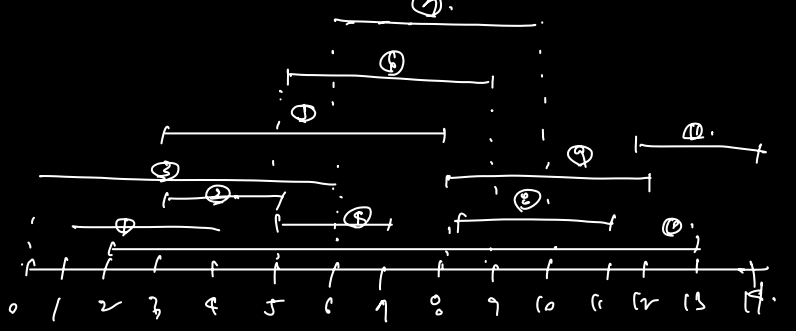
Greedy 정답: 1, 4, 8, 11
정답 알고리즘이 따로 있다(귀류법) :
상대가 주장한 정답을 내 정답으로 바꿔보자.
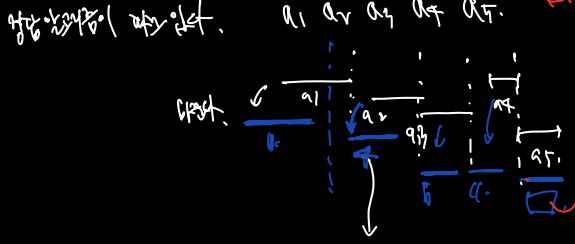
- 1번 강의 다음을 A라하고
- a1 강의 다음 강의들을 B라하면
- A가 B를 포함한다. (A다음 강의들이 B다음 강의들보다 같거나 빨리 끝난다.)
- 따라서 이렇게 끝까지 바꿨을 때 a_5에 주목해보자. a_4보다 먼저 끝난 강의를 내가 골랐고, a_5와 같은 것이 존재했다면 내가 뽑았을텐데 뽑지 않았다. (모순) 따라서 a_5 와 같은 것은 존재하지 않는다! (귀류법)
코드를 보자. (S, F는 각 강의가 시작하는 시간과 끝나는 시간을 저장한 배열이다.
Greedy_lecture_selcetor(S, F):
F.sort() # 끝나는 시간을 먼저 끝나는 순서대로 sort한다.
L = [0] # L은 우리가 반환할 선택한 강의의 인덱스이다
k = 0 # i와 k의 인덱스가 동시에 돌 것이다. k는 끝나는 시간의 인덱스로, i는 강의 시작 시간의 인덱스로 들어간다
for i in range(1, n): # i = 1-n 시작 시간 배열을 돌며
if S[i] >= F[k]: # 만약 끝나는 시간보다 큰 숫자가 나오면 그 수업은 넣는다. (넣은 수업의 F는 다음으로 가장 빨리 끝나는 수업일 것이다.)
L = L.append(i) # 고른 수업이므로 인덱스를 넣고
k = i # 이제 현재 넣은 수업이 끝나는 시간 다음의 수업을 찾는다.
return L
이 주어지면 L = [0, 3, 7, 10] (선택한 강의의 인덱스임) 을 반환할 것이다.
🔨 사다리타기
다음과 같이 정렬된 숫자가 있을 때 사다리타기 하여 (자리바꿈) 정렬하는 문제를 떠올려보자.
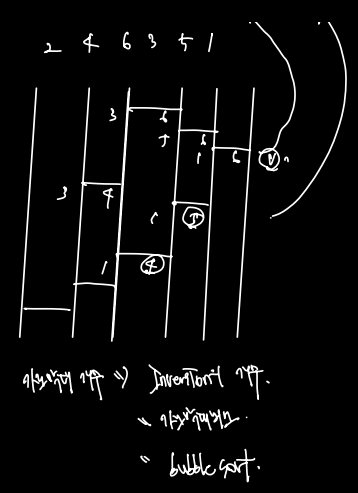
- 이렇게 랜덤한 숫자를 주고 sort 하는 최소 사다리개수를 반환하도록 하는 문제의 경우
- 필요한 가로 막대 개수는 Inversion 개수라 했다
- 정확히 Inversion 개수일 때만 가로 막대가 최소가 되는 경우이며 (더 많이해도 정렬할 수는 있으나)
- 이는 Bubble sort 의 아이디어와 비슷하다!
- 시간복잡도의 경우 가로 막대 수를 출력하라는 경우 앞서 봤던 거 같이 inversion 개수 = bubble sort 교환 연산 = O(n^2) 이지만 merge sort 를 생각해봤을 때 O(nlogn)에도 가능하다
- 그러나 가로막대 위치까지 모두 출력하려면 최대 가로막대 수에 맞춰 n(n-1)/2 만큼의 시간이 든다. O(n^2)
2 1부터 n까지 차례로 들어가고, 임의의 출력도 이미 주어진 상태에서 출력이 그대로 유지 되도록 하는 막대 개수를 최소로 하려면 (막대를 몇 개까지 지울 수 있는지)
Greedy 방법을 사용하자🔽
거꾸로 올라가면서 임의의 순열에서 1-n으로 사다리를 올라가면서 Inversion 을 없애는 사다리만 남겨두자.(결과 1-n을 만드려면 inversion 을 없애야 하기 때문)
만약 inversion 을 없애는 사다리라면 놔두고,inversion을 없애지 못하는 사다리라면(inversion 을 생성하는 사다리라면) 불필요하므로 삭제한다.

- 시간 복잡도 O(n^2 + 가로 막대수)
🔨 Huffman Code 계산문제
문자열을 숫자로 바꾸는 알고리즘을 효율적으로 짜보자 하는 문제이다.

a-f까지의 문자열을 바꾼다고 하고, 고정 길이 코드라 했을 때 1 글자에 무조건 3bit 씩 할당하게 되므로 100글자가 등장하면 100 charaters X 3 bit = 300 bit 이다.
그러나 가장 오른쪽 가변길이 코드와 같이 만들면 다음과 같은 계산이 적용 가능하다.
- 43 1 + (13 + 12 + 16) 3 + (9 + 7) * 4 = 250 bit 이므로 비트 수 절약이 가능하다.
왜 가장 오른쪽 같이는 안될까?
abc => 0101100 으로 변환가능하나 0101100을 보고 어떤 문자열인지 확정할 수 없다. 따라서 어떤 코드가 다른 코드의 prefix 에 등장하지 않도록 하는 코드가 필요하며, 이를 prefix-fee code라 한다.
기본적인 비용 계산은 다음과 같이 이루어진다.
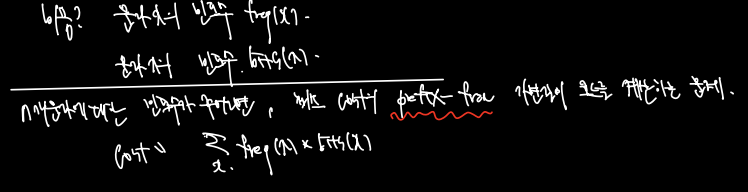
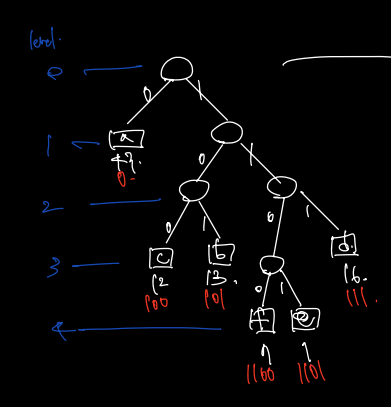
이러한 prefix free 코드를 만족하기 위해 decode tree 가 필요하다. 길이가 다른 코드 간에 모두 다른 트리를 타고 내려가기 때문에 prefix 에 절대 등장하지 않는다.
decode tree 는 그 자체로 1. prefix free code 를 만족하는데 그 중에서도 2. 비용을 최소화 하는 나무를 구해야 한다.
(생각해볼 점? 왜 Decode tree 는 무조건 prefix free code 를 만족할까? Decode Tree + bit 지정을 무조건 leaf 노드로 했을 때 그렇게 된다는 것이다. 이 경우 확정된 가변길이 비트는 더이상 자식이 없고, 따라서 본인을 prefix 로 하는 다른 비트가 없음을 의미한다.)
하나의 문자에 할당된 bit 수는 결국 트리에서 트리의 레벨 (depth) 이며, 다음과 같이 바꿀 수 있다.

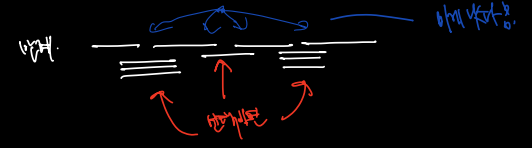
따라서 1. decode 트리로 구성해 prefix free code 를 만족시키되 2. 그 중에서도 빈도수가 높은 단어는 얕은 곳에, 많은 단어는 상대적으로 깊은 곳에 배치하자. (어떻게? > 빈도수가 작은 것을 먼저 묶으면서 위로 올라가면 된다.!)
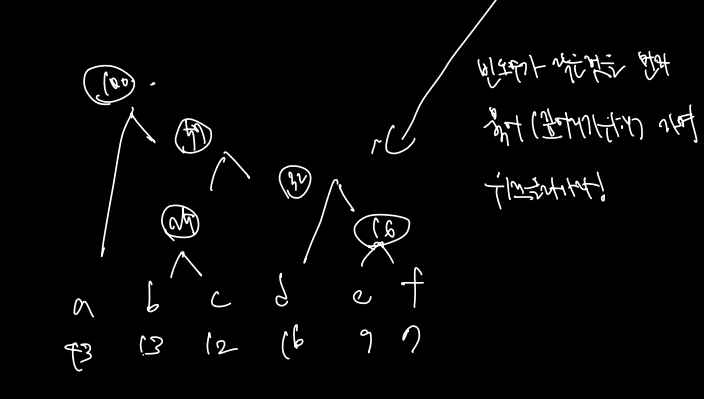
- import heapq
- h = []
- heappush(h, key): h 힙에 key 삽입, (h, (key, value)) 가능
- heappop(h): 최소값을 지우고 리턴
- h[0] 힙의 최소값
이를 이용하여 코드를 완성시킬 수 있음!
import heapq
H = []
for x in range(n): # nlogn
heappush(H, (f[x], 'x')) # (빈도수, x) 로 모두 힙에 저장
while len(H) > 1: # nlogn
a = heappop(H) # 가장 작은 빈도수
b = heappop(H) # 그 다음 작은 빈도수
heappush(H, (a.f + b.f, '(a.x b.x)'))
tree_string = heappop(H)[1] - 아마 nlogn 의 시간이 들 것이다.