Bayesian Optimization

Bayseian Optimization 문서

• 미지의 함수가 반환하는 값의 최대값을 매우 짧은 반복을 통해서 찾아내는 최적화 방식
• Gaussian process 를 통해 함수의 사후 분포를 생성하고 이를 기반으로 최적화하려는 함수를 재구성
• 많은 입력값을 받아서 수행, 사후 분포가 점점 개선, 함수 반환 값을 최대(최소) 되는 입력 파라미터 영역을 확실하게 찾게 됨.

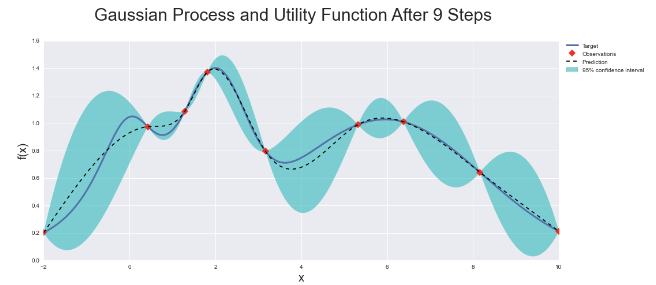
최적화

입력 값 범위

pbounds = {'x': (2, 40), 'y': (-3, 30)}

많은 x, y 입력 값 (실수범위임)

함수

def black_box_function(x, y):
return -x 2 - (y - 1) 2 + 1

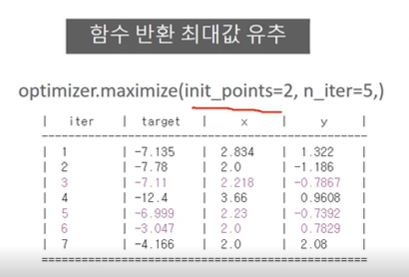
init_points : 초기 iteration
n_iter : 최종 iteration

Bayesian optimization 실습

pip install bayesian-optimization

x,y 데이터 기반 특정 값 반환하는 함수 생성
그냥 함수 하나를 무작정 만들어보자.

# 범위를 가지는 x, y 데이터를 기반으로 특정 값을 반환하는 함수.
# Bayesian optimization 은 넓은 범위의 입력값들을 이 함수에 입력했을 때 어떤 입력값이 이 함수를 최대화 하는지 추론.
def black_box_function(x, y):

    return -x ** 2 - (y - 1) ** 2 + 1

입력 파라미터들의 범위 설정

# 입력 파라미터들의 범위(공간)
pbounds = {'x': (2, 4), 'y': (-3, 3)}

객체 생성, 반환값을 최대화할 수 있는 입력 파라미터 값과 반환값 탐색

from bayes_opt import BayesianOptimization

# 최적화할 함수와, 입력 파라미터의 범위를 입력 받아서 BayesianOptimization 객체 생성 
optimizer = BayesianOptimization(
    f=black_box_function,
    pbounds=pbounds,
    random_state=1
)

# 함수 반환값을 최대화 할 수 있는 입력 파라미터 값과 반환값을 iteration하면서 최적 검색 
optimizer.maximize(
    init_points=2, #초기 랜덤하게 반복
    n_iter=5, #최적화 총 반복 
)

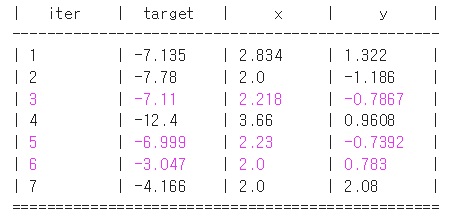
iter 6 번의 target 이 최대가 되는 지점을 주목하면 된다. x 는 2, y 는 0.783이다.

순차적 탐색 로직과 비교

import numpy as np

result = -9999
x_val = -9999
y_val = -9999
iter_count = 0

for x in np.arange(2, 4.1, 0.1): #2에서 4까지 0.1씩 
    for y in np.arange(-3, 3, 0.1): #-3부터 2.9까지 0.1씩 
        current_result = black_box_function(x, y)
        iter_count += 1
        if current_result > result: #최댓값 찾는 반복문 
            result = current_result 
            x_val = x #그때 X
            y_val = y #그때때 Y

print('iteration count:', iter_count, 'max result:', result, 'x value:', x_val, 'y value:', y_val)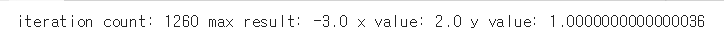

반복문 1260을 돌았으며, 성능도 y값을 보았을 때 낮다.

범위 넓혀서 수행 비교

# 입력 파라미터들의 범위(공간)
pbounds = {'x': (2, 40), 'y': (-3, 30)}

optimizer = BayesianOptimization(
    f=black_box_function,
    pbounds=pbounds,
    random_state=1,
)

optimizer.maximize(
    init_points=2,
    n_iter=10,
)

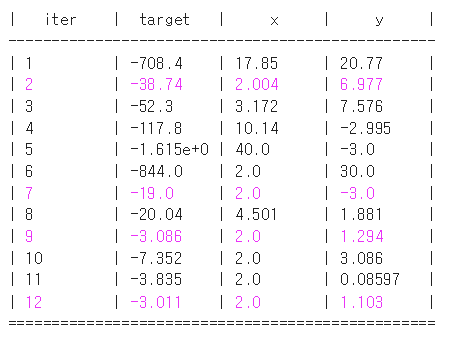
iter 9번이 최대이다.

import numpy as np

result = -9999
x_val = -9999
y_val = -9999
iter_count = 0
for x in np.arange(2, 40.1, 0.1):
    for y in np.arange(-3, 30, 0.1):
        current_result = black_box_function(x, y)
        iter_count += 1
        if current_result > result:
            result = current_result
            x_val = x
            y_val = y

print('iteration count:', iter_count, 'max result:', result, 'x value:', x_val, 'y value:', y_val)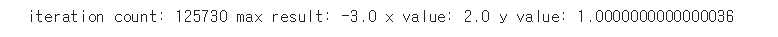

반복문 125730을 돌았다.