[NLP] Computing Gradient in Recurrent Neural Network

Recurrent Neural Network

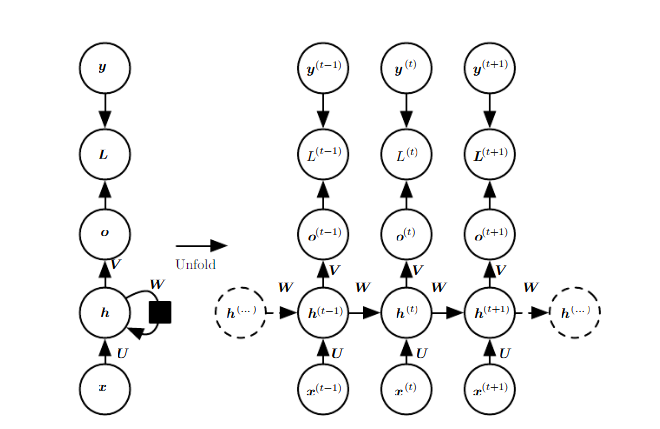
Examples of important design patterns of RNN

• RNN that produce an output at each time step and have reccurent connection between hidden units (h 사이 연결)
• RNN that produce an output at each time step and habe reccurent connections only from output at one time step to the hidden units at the next time step (output -> input)
• RNN with recurrent connection between units, that read an entire sequence an then produce a single output

가장 일반적인 것이 첫번째 경우인 hiddent 간의 연결된 RNN 이므로 이경우의 forward 연산을 그림으로 표현하면 다음과 같다.

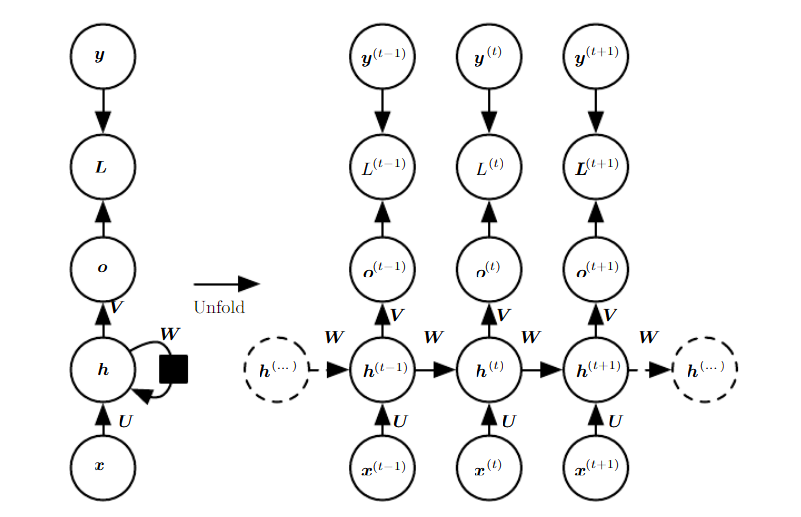
Forward propagation quations for the RNN

위 그림에서 표현된 RNN을 수식으로 변환해보자.

• hyperbolic tangent activation function
• discrete output (predict words or characters)
• begins with a initial state $h^0$.
• time step t=1 부터 끝까지.

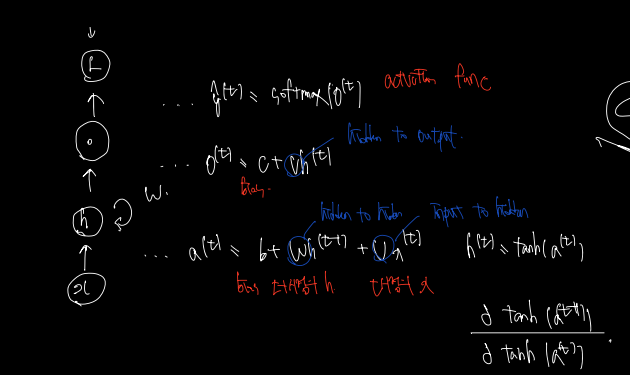
• b, c: bias vectors
• U, V, W: weight metrics (input-to-hidden, hidden-to-output, hidden-to-hidden)

Total loss

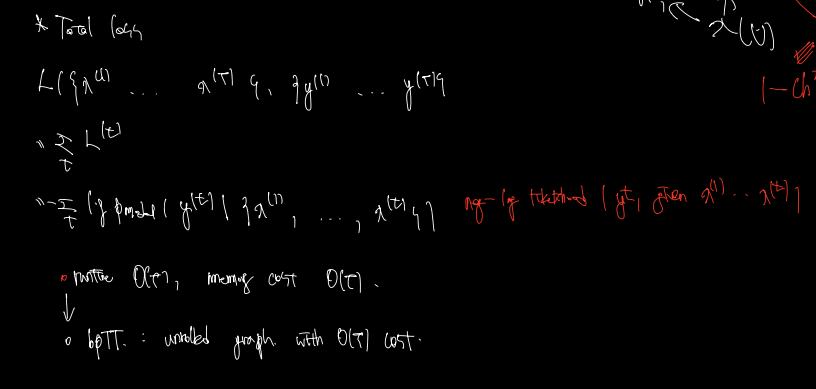
Total loss 는 위와 같다.

• maps an input sequence to an output seqence of the same length
• given sequence of x values paired with a sequence of y vlaues
• sum of the losses over all the time steps
• L is the negative log-likelihood of y, given x

이렇게 unrolled graph 된 그래프에서 역전파하는 걸 backward propagation 이라한다. 이경우, runtime 은 $O(\tau)$ 으로 결코 줄여질 수 없다는 것이 특징이다. (병렬 연산이 안된다) 왜? 이전 계산 결과값이 있어야 그걸 가지고 forward 전파 연산을 하기 때문이다. 마찬가지로 backward 연산에서도, memory cost 는 $O(\tau)$ 로 같다. 이렇게, unrolld graph 에서 펼쳐지는 $O(\tau)$ 만큼의 비용이 드는 backward-propagation 을 back-propagation throuht time(BPTT) 라 한다.

Teacher Forcing?

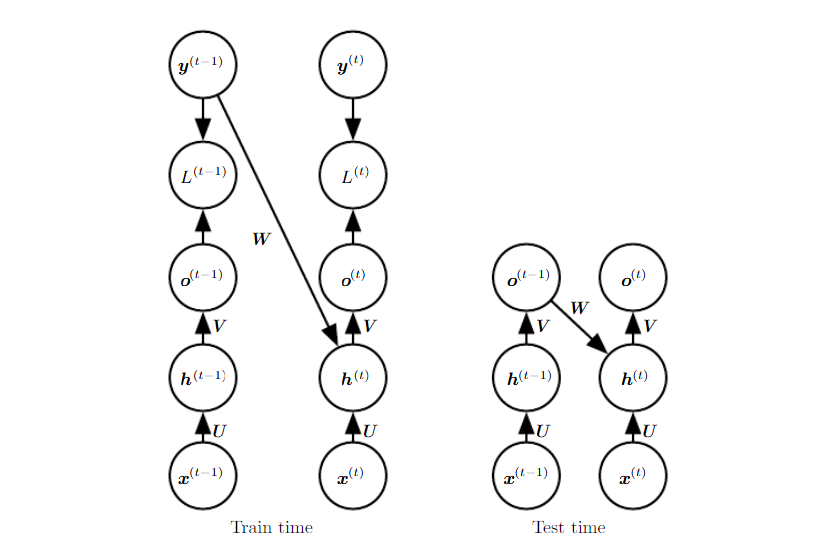
그러나 이전에 살펴본 RNN의 가짓수 중 두번쨰에 해당하는 것 (output at one time step to the hieen units at the next time step) 또한 살펴볼만하다. 이전까지는, hidden-to-hidden 연결이 없기에 다음의 문제를 낳았다.

• 결과값 자체가 과거 시퀀스의 정보를 담아내야한다 (그러기 어렵다)

그러나 상대적 장점 또한 있는데, 그건 바로 eliminating hidden-to-hidden recurrence 에서 오는, loss 계산의 어려움을 삭제할 수 있다는 것이다. (훈련 자체가 병렬화가 가능, gradient for each step t computed in isolation) 이전의 hidden cell 에서 내려온 값을 이용하여 계산하지 않으므로 -> 그 값을 역전파할 이유도 없고 -> 따라서 계산시 가미된 값인 시점 t에서 시점 t에 계산에 가담한 값만 역전파하면 된다.

이렇게, Reccurent 하게 계산을 하는데 이전 시점의 output 이 현 시점의 input 으로 들어가며 훈련하는 방법을 teacher forcing이라고 한다. 다시말해, teacher forcing 에서의 인풋은 이전 시점의 y값(ground truth) 과 현 시점까지의 x값이다. 이를 수식으로 정리하면 다음과 같다.

< conditional maximum likelihodd criterion, teacher forcing. >

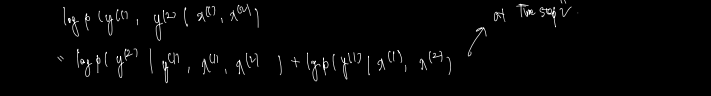
• time t=2 에서의 값이다
• model 은 시점 2까지의 x 입력과 1의 y gt 값을 보고 conditional probability of y(2) 를 maximize 하도록 훈련될 것이다.
• 훈련은 위와 같이하고, 예측은 (위)의 사진처럼 h를 계산할 때 실제 값은 가리고 ouput O와 x 를 가지고 결과를 예측한다.

Computing the Gradient in a RNN

다시 main RNN (hidden to hidden connection) 으로 돌아와서, 이때의 Gradient Computing 을 해보자.

• parameters U, V, W, b
• nodes x(t), h(t), o(t), L(t)
• 각 node 를 Loss 를 가지고 미분

1) final loss

전체 loss 를 해당 시점 t의 loss 로 편미분한 값은 다음과 같다.

2) O(t) Gradient

그다음으로 가장 최근에 가담한 값인 O(t) 에 대해 미분해보자. 결과는 다음과 같다.

o(t) -> L(t) -> L 순으로 계산되었으므로 사이에 값이 하나 더 들어간다. 어차피 1이므로 뒤의 식만 계산한다.

3) h(t) Gradient

그 다음으로 최근에 가담한 값은 h(t) 이다. h(t) 의 경우는 계산해야 할 값이 2가지이다. t+1 시점의 h(t+1) 을 미분해서 오는 backward 편미분값도 받아야하고, t시점의 O(t) 에서 내려오는 편미분값도 계산해야 한다. (둘을 더해주면 된다.)

여기서 또다시 케이스를 나눌 수 있는 것이, 마지막 시점 $\tau$ 의 경우 t+1 시점에서 오는 편미분 값이 없다. 따라서 다음과 같이 간단하게 계산된다.

Case 1)

loss 를 o(t) 로 편미분한 값에,(o(t) 가 가지는 편미분 값에) h -> o 를 계산할 때 썼던 식에서 h의 계수로 V가 있으므로 이를 곱해주도록 한다.

Case 2)

케이스 2의 경우는 t = 1 부터 마지막 시점 -1 까지의 조금 더 일반적인 상황이다. 이때는 양쪽에서 오는 편미분 값을 모두 고려해야한다고 했다. 앞쪽에 더해진 값이 h(t+1) 에서 오는 편미분 값이고 (이는 h(t), h(t+1) 의 연결과 h(t+1) 이 가지는 편미분 값을 포함한다.) 두번째 더해진 값이 O(t) 에서 오는 편미분 값이다.

이떄 첫번째 더해지는 값인 h(t+1), h(t) 사이 미분에서 diag는 뒤 수식의 diagonal 된 version 을 뜻하며, jacoboilc hyperpoclie tangent 의 미분이 포함된다. tanh 를 미분하면 다음과 같은 수식이 된다.

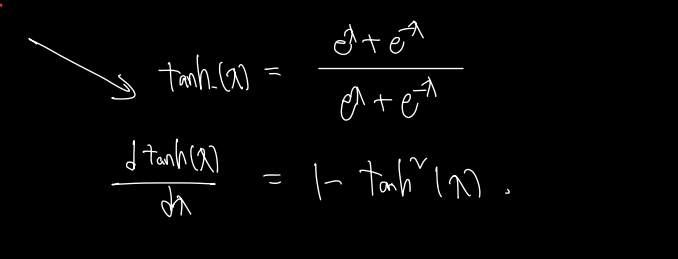
4) Remaining parameters

1, 2. c와 b bias 에 대한 역전파값을 최종적으로 구해보자.

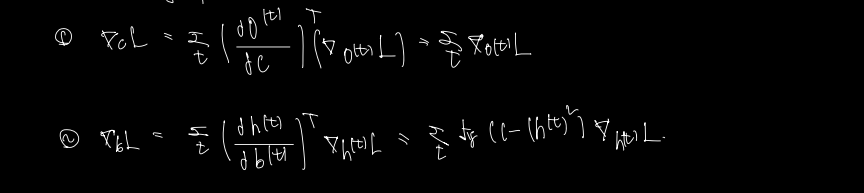
1) c 의 역전파값은 o(t)의 편미분값과 o(t)를 c에 대해 편미분한 값을 곱하면 된다.
2) b 의 역전파값은 h(t) 의 편미분값과 h(t) 를 b에 대해 편미분한 값을 곱하면 된다. b에서 h를 구할 땐 tanh 이 가담하므로 이를 미분한다.

3, 4, 5. V, W, U 값을 최종적으로 구하면 다음과 같다.

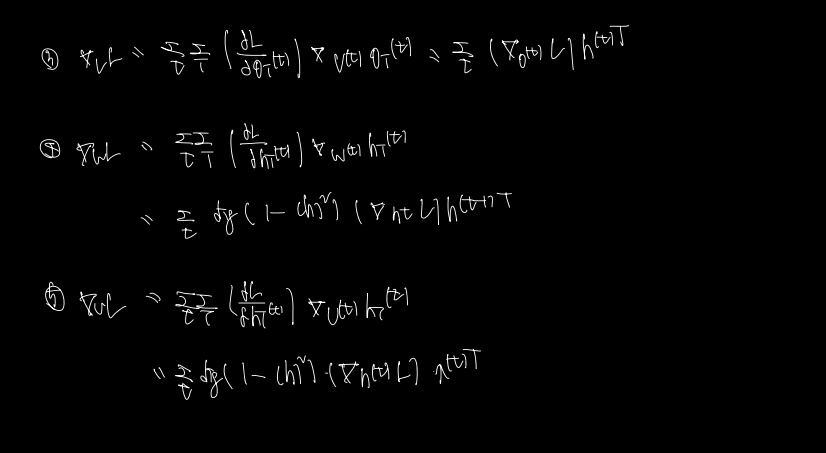
3) V 의 역전파를 구할 땐 o(t) 의 편미분값과 o(t) 에서 v로 오는 편미분값을 곱한다. 이 값은 h(t) 이다.

4) W 의 역전파를 구할 때는 h로 오는 편미분값과 h(t)에서 w로 오는 편미분값을 곱한다. 후자의 경우 h(t-1) 과 tanh 의 미분값이 곱해진다.

5) U 의 역전파를 구할 때는 h로 오는 편미분값과 h(t)에서 U로 오는 편미분값을 곱한다. 후자의 경우 x(t) 와 tanh 의 미분값이 곱해진다.