Smoothing & back off
smoothing, back off 은 language modeling 시에 unigram, bi gram, tri gram 에서 발생하는 zero probability 문제를 해결하기 위한 것이다. 만약 코퍼스 내에서 co-occurence 값이 0이라면 이들 사이에 곱 연산이 무의미 해지는데, 따라서 곱해지는 값이 0이 되지 않도록 각 단어의 확률에 대한 조정을 가하는 방법론이다. 3가지 방법으로 요약이 가능하다.
- Laplace smoothing
- Backoff smoothing
- kneser-ney smoothing
1. Laplace smoothing
가장 단순한 방법으로, co-occurence 분자 값에 1또는 실수를 더하는 방법이 있다.
1) Add one (in uni-gram)
첫번째 방법으로는 Add one 이라고 하는 것이 있으며, 아래는 uni-gram 에서 동작하는 예시이다.
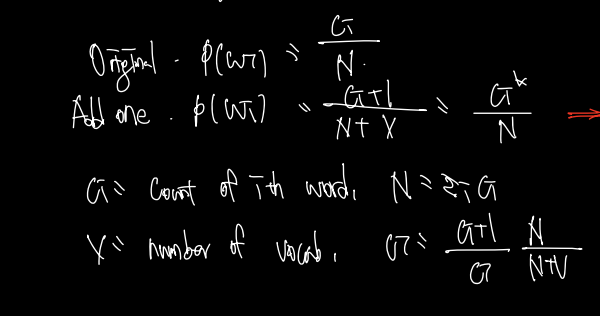
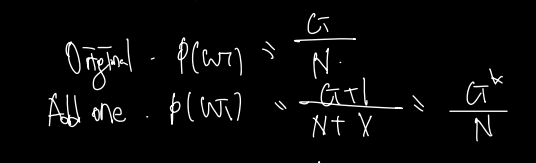
original 한 방법으로 전체 수 N에 대한 i번째 구하려고 하는 단어의 카운트를 구했다면, add one 에서는 단어의 카운트가 0이 되는 것을 방지하기 위해 단순히 1을 더하게 된다.
그러나 Add one 의 경우 0인 co-occurences에서만 동작하는 것이 아니라 전체에 대해 +1을 하게 되므로 Add one 으로 계산된 값이 0이 아닌 다른 값에 대해선 전체 값이 감소하게되는 효과가 있다. (+V) 따라서 이를 discount라고하고, 이 비율을 discount ratio라 하는데, 식으로 표현하면 다음과 같다.

2) Add-k smoothing
두번째 방법으로 add-k 방법이 있는데, 분자에 1 대신 k만큼의 수를 정해서 더하는 방식이다. k 는 보통 0.2, 0.5 등 1보다 작은 실수로 계산된다. 아래와 같은 식을 쓸 수 있다.
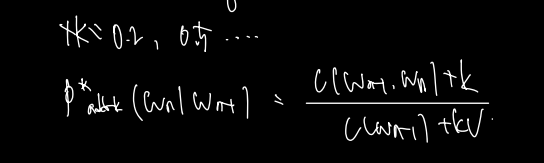
2. Back off and Interpolation
다음으로 소개할 두 방법은 분자에 수를 더했던 Add 방법과는 다르게 n-gram 의 order 를 조작하는 방법이다. 하나씩 보자.
1) back off
첫번째인 back off 는 전체 계산이 아닌 zero probability 가 발생할 때 해당 계산을 적용함을 염두에 두자. 만약 코퍼스 내에서 계산 시에 zero probability 가 발생한다면, n-gram 의 order 을 하나 내려서 계산한다. 예컨대 tri-gram 에 해당하는 단어 말뭉치가 코퍼스에 있을 확률이 bi-gram 보다 희소하므로, tri-gram이 count = 0 이라면 bi-gram 으로 낮춰서 계산하자는 것이다. 이를 식으로 표현하면 다음과 같다.

그러나 이렇게 n-gram order 을 바꿔가며 계산할 경우 특수한 경우에 합이 1이 넘는 불상사가 발생할 수 있다. 따라서 이 경우를 방지하기 위해 도입된 계산을 katz back off라 하는데, 위의 식에 확률 또는 function 을 곱해서 discounting, 즉 1 이하의 값으로 유도하는 방법이 있다.
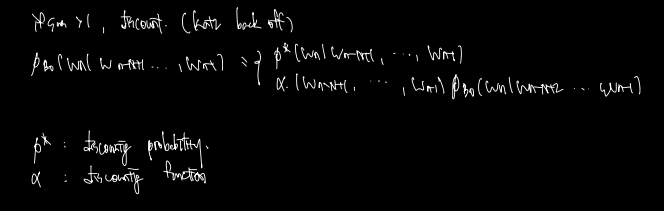
여기서 asterisk p, alpha 를 계산하는 방법은 또다시 존재하나 따로 다루지는 않겠다.
2) Interpolation
다음으로 소개할 방법은 해당 n-gram 의 계산을 Linar combination으로 연결하는 것이다. 아래와 같이 tri-gram 을 계산하기 위한 original 식을 람다를 붙인 tri, bi, uni gram 으로 각각 표현할 수 있다. 이 경우에 람다1,2,3 의 합은 1이다.

Kneser-ney smoothing
다음 Kneser-ney smoothing 방법을 이해하기 위해선 우선 Absolutee discounting 을 알아야한다.
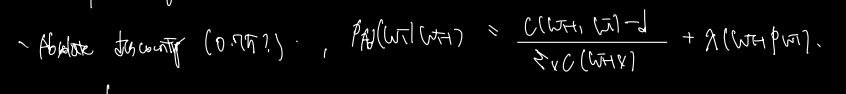
이전 단어가 등장할 때 다음 단어가 등장할 확률을 구하기 위해 C(wv)의 시그마를 분모로, c(Wi-1, W) 을 분자로 하는 것은 익숙한데 d 값은 왜 빼는 것일까? d 값은 아래 표에서 이해할 수 있다.
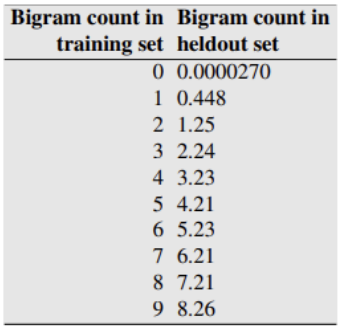
어차피 n-gram, smoothing 의 목표는 현재 데이터셋에서 계산한 값이 held-out set 에서도 잘 동작하도록 의도된 것인데, 실제 220만개 데이터를 가지고 계산해보니 위와 같은 경향성이 나타난 것이다. train set 에서 uni-gram의 등장횟수는 0, 1을 제외한 위의 등장에서, 0.75 정도를 뺀 counting이 held-out set에서 등장횟수와 거의 일치했다는 것이다. 따라서 위의 식은 uni-gram 확률을 구하는데 있어서 본래의 식에 held-out set 와의 경향성을 고려해 d만큼을 뺴주고, uni-gram interpolation 을 적용한 결과다.
본격적으로 Kneser-Ney smoothing 의 식을 보면 다음과 같다. 마찬가지로 absolute discounting 을 적용하는 것 같지만 식이 같지는 않고 분모에 continuation 확률이란 것이 있다.
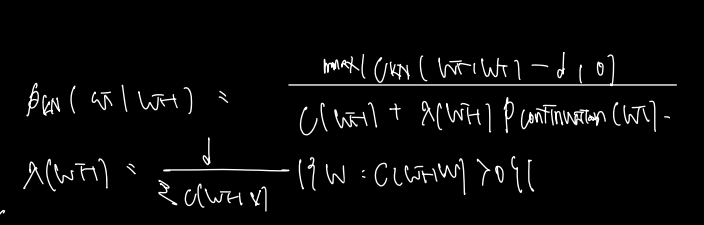
continuation 확률이란 뭔가? uni-gram 으로 단어 하나만 보면서 계산할 때, context 를 계산하지 못하는 문제가 있는데 (단순 많이 등장한 단어가 뽑히므로) 이를 방지하기 위해 w continuation 확률이라고 한다면 w가 bi-gram 에서 두번째로 등장하는 count를 bi-gram 전체 카운트수로 나눠주는 것이다. 따라서 kneser-ney smoothing 이란 absolute discounting 에 uni-gram 이 아닌 continuation 확률을 고려한 것으로 이해해자.
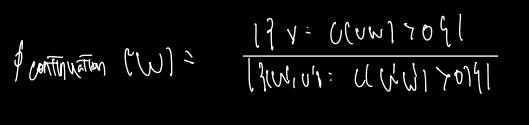
위에서 등장한 Pkn은 bi-gram에 관한 식으로 이를 일반화하면 다음과 같은 식을 얻을 수 있다.
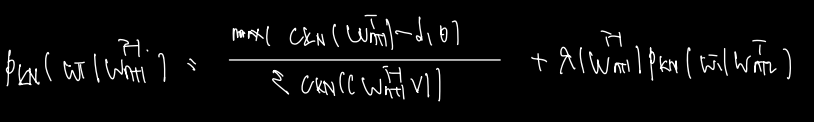
absolute discounting, back off 이 모두 들어가 있는 식으로 정리가 된다. 앞쪽에 absolute discounting 에 대한 식은 동일하다. (bi-gram이 일반화된 식으로 정리된 것 뿐이다. 뒤쪽에 더해진 값은 Pkn 을 구할 때 Pkn w n+1부터 i-1값이 주어질 때 wi의 확률을 pkn w n+2부터 i가 주어질 때 i의 확률로 전환한다. 이는 back off 의 아이디어와 동일하고, 이를 recursive 하게 전개함으로써 hider order 에서 보지못한 n-gram 에 대한 카운트를 람다와 함께 보정하여 계산할 수 있도록 하는데 그 의도가 있다.