[HUFS/Algorithm] LCS, Edit distance, 행렬 곱셈, LIS

DP를 활용한 문제들

📚 목차
1. LCS 문제
2. 편집거리
3. 행렬 곱셈
4. LIS

1. LCS

LCS 란 Longest Common Subsequence 의 약자로 주어진 문자열 2개가 주어질 때 두 문자열 내의 문자를 뽑아 만들 수 있는 최장 길이의 공통 부문자열, 길이를 반환하는 문제이다.

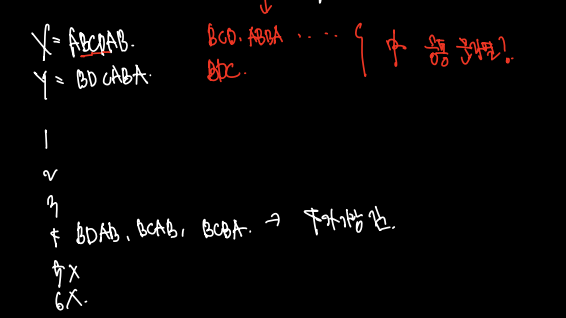
1. 해를 분석하자.
   주어진 문자열 X = 'ABCBDAB' Y = 'BDCABA' 라 할 때 LCS 는 4이다. 따라서
   LCS(X7, Y6) = 4 와 같이 표시할 수 있다. 이때 x7과 y6가 각각 B, A 로 서로 다른 문자이므로 마지막 수를 동시에 뽑을 수 없다. 따라서 마지막 두 문자가 다를 때 다음과 같이 쓸 수 있다.

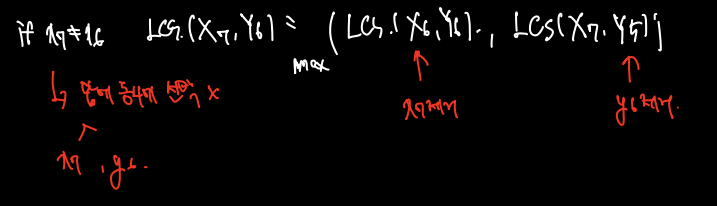
x7을 선택하지 않고 X6, Y6까지 본 것과, y6를 선택하지 않고 X7, Y5까지 본 것 중 긴 길이와 같다는 것이다.

만약에 문자열 끝이 같다면 무조건 포함하면 되니까 다음과 같이 적는다.

(뒤에 +1까지 붙여주는 게 맞다.)

2. 점화식을 세우자
   

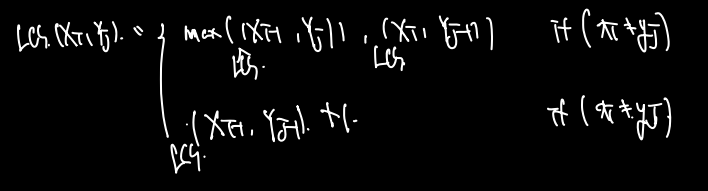
일반화하면 다음과 같다. 아래의 식은 if (xi == yj) 로 수정한다.

3. DP 테이블을 정의하자.
   인덱스를 두개씩 사용하고 있으므로 2차원 배열 형태의 DP 테이블을 정의해볼 수 있다.
   

DP테이블에 대한 내용은 다음과 같다.

• 각 문자 앞에 0인덱스도 추가하여 행, 열 0번은 모두 0으로 채운다.
• i,j 가 다르면 계산한 것과 같이 왼쪽(위의 그림에선 왼쪽으로 이동하는 것이 Xi, Yj-1 의 상황), 위쪽(Xi-1, Yj) 중에서 max 를 선택하여 데려온다.
• i, j 가 같으면 무조건 선택하고 하나씩 감소시킨 것(그 전 문자열까지의 최장길이)을 그냥 더하면 된다.
• 모든 테이블을 채운 후 마지막 [-1][-1] 의 숫자가 답.

채우는데 걸리는 시간은 1이므로 길이가 n, m 이라 했을 때 O(nm) 만큼의 시간이 걸린다.

역추적해 올라간다면 같을 경우 왼쪽 위로, 같지 않을 경우 두 가지 방향을 고려하여 O(n+m) 의 시간이 걸린다.

<코드>

• 총 걸리는 시간 O(n^2)

2. Edit Distance Problem

X = HUMAN
Y = CHIMPANZEE 가 주어지면, 삽입 6개와 삭제(u) 1개로 인간이 침팬지가 될 수 있다.

이 문제를 풀기 위해선 X에만 있는 것은 삭제해야 하고, Y에만 있는 것은 삽입해야 하는데,
삽입, 삭제, 교체에 드는 비용을 다음과 같이 나타내 볼 수 있다.

결과적으로 Edit Distance 는 문자열 X가 삽입과 삭제, 교체를 거쳐 Y가 되기 위해 필요한 최소비용을 말한다.

DP[i][j] 를 문자열 X_i를 Y_j로 바꾸는 비용이라 할 때, DP[i][0] 은 문자열 X_i를 Y_0으로 바꾸는 비용으로 삭제 비용이고, DP[0][j] 는 문자열 X_0을 Y_j로 바꾸는 비용으로 삽입비용이다.

DP문제는 현재 주어진 문제 Xi, Yi를 작은 문제로 쪼개는 것으로 i-1, j-1 이 근처를 보면 되고 가능한 경우의 수는 삭제, 삽입, 교체이다.

1. Xi 삭제
   W_del(Xi) + DP[i-1][j] : 삭제를 하는 비용 + 나머지 Xi 를 제외한 비용

2. Yj 삽입
   DP[i][j-1] + W_ins(Yj)

3. Xi => Yj 교체 비용
   DP[i-1][j-1] + Wsub(Xi, Yj)

DP[i][j] = min(1, 2, 3) : 모두 계산한 후, 가장 최소를 반환

따라서 DP테이블을 살짝 그려보면 i, j를 정할 때 바로 위 + 삭제비용, 바로 왼 + 삽입비용, 대각선 왼쪽 + 교체비용 중 최소값을 가져오면 된다.

3. 행렬곱셈 (비용을 최소로, Matrix Multiplication)

다음과 같이 일반적인 행렬 곱셈을 하는 경우 한 칸을 계산하는데 O(q), pr 칸의 계산이 필요하므로 총 O(pqr)의 시간이 걸린다.

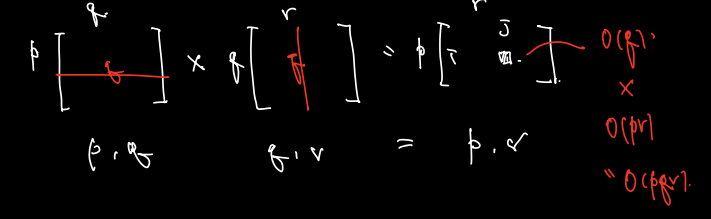
아래의 경우는 어떨까? M1, M2, M3 크기가 다른 세 개의 행렬이 주어질 때, 같은 곱셈이라도 어떻게 괄호를 묶느냐에 따라 드는 비용이 다르다. (다음의 경우에선 오른쪽이 훨씬 유리하다.)

따라서 일반화하여 M1, M2 .. Mn의 n개 행렬의 곱셈이 차례로 주어질 때 행렬곱셈의 비용을 최소화하는 것은 최소비용이 되도록 괄호를 묶는 일과 같으며, n = 4일 경우 끝까지 괄호치는 경우의 수는 5개이다. (5개 중 1개를 고르는 문제.왜 5개인지 생각해보자)

사실 이 숫자는 Catalan Number 와 일치하며 지수식이 되어 매우 큰 수이므로 DP로 해결해보자는 결론.

다시 M1, M2, M3, M4 의 네 개 행렬로만 돌아와서, 마지막 연산을 관찰하면 다음과 같을 것이다. DP[i][j] 를 Mi ... Mj 에 대한 괄호치기의 비용이라 정의하고, 최종적으로 DP[1][n] 을 구하자. (이때 Mk 는 Pk X Pk+1 행렬이다.)

1. M1 X (M2 M3 M4) => DP[1][1] + DP[2][4] + p1p2p5
2. (M1 M2) X (M3 M4) => DP[1][2] + DP[3][4] + p1p3p5
3. (M1 M2 M3) X M4 => DP[1][3] + DP[4][4] + p1p4p5

따라서 DP[1][4] 는 min(1,2,3)인데 조금 더 점화식답게 정리하자.

DP[i][j] = Mi부터 Mj까지의 행렬 곱셈에 드는 최소 비용, 중간에 Mk와 Mk+1을 지남
= min(DP[i][k] + DP[k+1][j] + PiPkPk+1)

• 이렇게 한 칸을 채우는데는 O(n) 의 시간이 걸릴 것이다.

DP 테이블을 그려보면 아래와 같다.

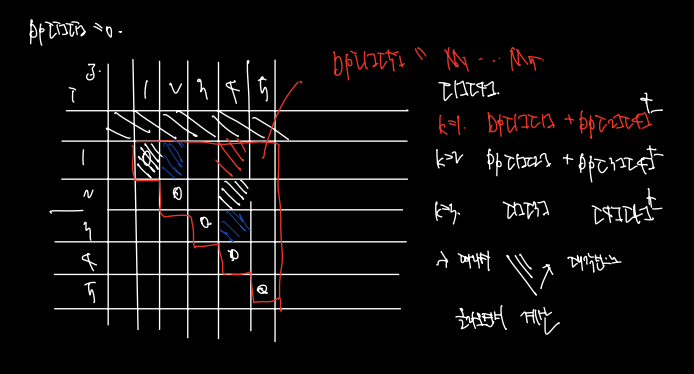
• 초기화는 DP[i][i] = 0 으로 하는 것이다. 예컨대 M1부터 M1 곱은 비용이 0이니까
• 현재 구하는 [1][4] 를 위해선 다음과 같이 세 값을 더하는 과정이 필요하다. (**각 DP식 끝에 PiPk+1Pj+1을 추가해주도록 하자.)
• 따라서 오른쪽 위 대각선으로 올라오면서 계산하는 구조이다.
• 수행시간 = 테이블 엔트리 수 X 엔트리 계산 시간 = O(n^2) X O(n) = O(n^3) 이다.

LIS (Longest Increasing Subsequence)

주어진 숫자 배열 A = [2, 8, 5, 10, 18, 13, 20, 4] 를 가지고 만들 수 있는 가장 긴 증가하는 부문자 배열을 찾자.

• LIS[i] 의 정의를 A[i] 로 끝나는 부수열 중 가장 긴 부문자 길이라 하고,

• 점화식을 LIS[i] = max(LIS[j] + 1) 이라 하면 된다.

• DP로 n^2에도, nlogn 의 시간에도 풀린다