DP
최대 구간 합
음수를 포함한 숫자 리스트 A가 주어질 때, 구간을 마음대로 설정해서 합이 최대가 되는 구간을 구한다고 하자. 이를 어떻게 DP 로 구할 수 있을까?
예시 배열은 A = [-2, 0, -1, 3, 2, -1, 2, -2] 이다.
Sol1) 모든 구간 (i,j) 에 대해 합 구하기: 구간은 i, j 로 총 n^2 개가 나오고, 구간을 구한 후 각 합을 구하는 sum 계산이 n이 걸린다. 따라서 O(n^3)
Sol2) prefix sum: prefix 배열을 새롭게 구해두면 구간만 설정하면 (n^2 구간개수) 이후는 차로 구하기 때문에 각각 1의 시간만 걸린다. 따라서 O(n^2)

Sol3) 분할정복
주어진 A 배열을 다음과 같이 L, M, R로 분할해보자.
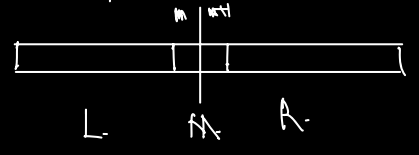
최대구간은 L,R,M 중 하나에 무조건 있다. 따라서 max(L, R, M) 을 반환하면 된다.
L, R 중 하나라면 재귀적인 방법으로 구하기 때문에 각각 T(n/2) 의 문제로 2T(n/2) 의 시간에 계산이 된다. M에 속한다면 위의 사진에서 인덱스 m과 m+1 은 무조건 포함이 된 상태에서 m에서 왼쪽으로 더해나가며 구하고, m+1에서 오른쪽으로 더해나가며 최대가 되는 구간을 구한다. 따라서 이 경우 cn 의 시간이 걸린다. 따라서
T(n) = 2T(n/2) + cn = O(nlogn)
Sol4) DP: O(n)
먼저 DP 문제를 풀기 위한 단계를 다음과 같이 정리해볼 수 있다.
1. 해를 분석한다. 주어진 문제를 작은 문제로 분할하는 과정을 의미한다.
2. 원 문제의 해를 작은 문제 해의 점화식으로 표시해본다.
3. 점화식을 세웠다면 이를 바탕으로 DP 테이블을 정의한다.
4. 맞는지 증명한다.
주어진 배열을 다시 보고 위에 인덱스를 표시해보자.
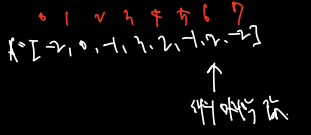
A 배열에서 인덱스 0, 1, 2 는 음수 또는 0이므로 일단 기대가 안된다. 그 후의 수를 살필 때 최대가 되는 구간을 다음과 같이 가정해볼 수 있다.
- 3이 끝나는 구간이 가장 큰 구간이 되는 경우
- 2가 되는 경우
- (-1)이 되는 경우
- 2가 되는 경우
따라서 다음과 같이 원 문제를 작은 문제의 점화식으로 표현할 수 있다.
A[i] 로 끝나는 최대구간 합 = A[i-1] 로 끝나는 최대구간 합 + A[i] 이거나 그냥 A[i]
DP테이블: DP[i] = max(DP[i-1] + A[i], A[i])
A[i] 가 max 가 되는 경우는 다음이 있겠지?
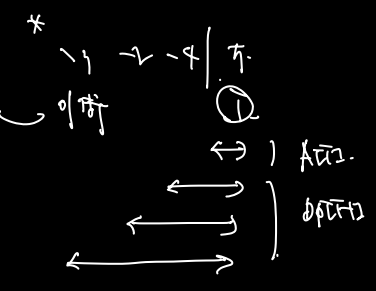
실제로 해보자.
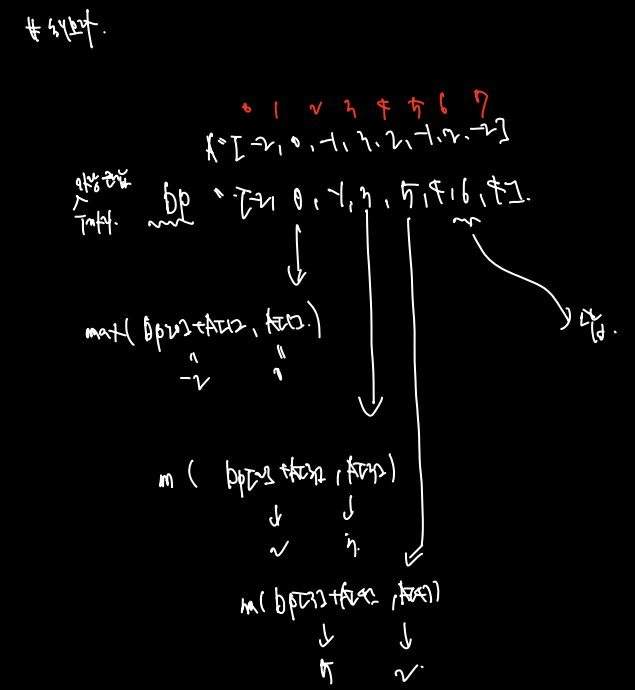
최종 답은 이런식으로 정의한 DP 테이블에서 최대값을 고르는 것이다. 왜 DP[n]이 아닌 max(DP)일까? DP[i] 자체를 A[i] 로 끝나는 (범위의 끝이 무조건 된다고 했을 때) 구간에서의 최대 합이라 정의했기 때문이다. 따라서 DP[n] 은 A[n] 를 무조건 포함한다는 것인데, 그럴 필요도 없으며 그렇게 하면 안된다.
마지막으로 코드를 보자.
DP = [0]*len(A)
DP[0] = A[0]
for i in range(1, len(A)):
DP[i] = max(DP[i-1] + A[i], A[i])
return max(DP) Zig-Zag 수열찾기
zig-zag 수열찾기란 주어진 숫자 배열 A에서 숫자를 선택했을 때 이전 숫자보다 큰-작은-큰 ... 숫자를 반복하도록하는 Zig-Zag 수열을 찾는 것이다.
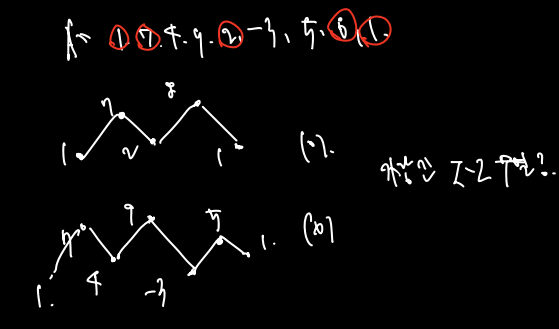
이 문제는 원 문제를 두 가지로 나누어 생각할 수 있다.
- 지그재그로 움직이다 마지막엔 이전 수보다 작은 수low로 끝나는 가장 긴 수열
- 지그재구로 움직이다 마지막에 이전 수보다 큰 수high로 끝나는 가장 긴 수열
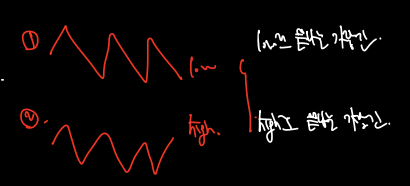
이를 바탕으로
A[k]가 high 로 끝나는 가장 긴 지그재그 수열의 길이
= A[j]가 low로 끝나는 가장 긴 지그재그 수열의 길이 + 1 (단 A[j] < A[k], j<k)

j의 후보가 여러 개일때 수열이 가장 긴 것을 붙이자. 따라서
- high[k] = max(low[j] + 1) 이라 할 수 있다. 마찬가지로
- low[k] = max(high[j]+1)
- high[0] = 1, low[0] = 1
- 다 채우고 나면 return max(max(high), max(low))
각 high와 low 의 리스트를 정의한다고 했을 때
한 칸을 채우는데 n의 연산이 필요하며, n칸이므로 각각 O(n^2), 병렬적인 연산이므로 최종적으로도 O(n^2)
수도코드
high = [0]*len(A)
low = [0]*len(A)
high[0] = low[0] = 1
for k in range(len(A)):
for j in range(k):
if A[k] > A[j] and high[k] < low[j] + 1: #max 로 끝나고 현재 할당된 high[k]보다 큰 low[j] + 1이 있다면 (추가할 수 있다면)
high[k] = low[j] + 1
# high[k] = max(low[j] + 1)
if A[k] < A[j] and low[k] < high[j] + 1:
low[k] = high[j] + 1
# low[k] = max(high[j] + 1)
return max(max(high, low))