[HUFS/Algorithm] 4. Divide and Conquer

1. 분할정복 정의

원래 문제를 풀 수 있을 정도의 작은 크기의 부분 문제로 분할해 각각 해결 한 후, 부분 문제의 해답을 잘 모아 원래의 해답을 얻는 방법.

• 크기가 작아질 뿐 문제 자체는 변하지 않음 > 재귀적인 분할

• 재귀적인 분할이므로 수행시간 T(n) 은 점화식으로 표현

• Selection에서 학습한 quick_select, medians_of_medians 모두 분할정복 알고리즘들이다.

2. n개의 수 중 최대값 구하기

a. Sol1)

def find_max1(A):
	if len(A) == 1: return A[0] 
    else: return max(A[0], find_max1(A[1:])) 

b. Sol2)

def find_max2(A):
	if len(A) < 1: return -infinity
    elif len(A) == 1: return A[0] 
    else: return max(find_max2(A[:len(A)//2]), find_max(A[len(A)//2:])) 

c. 두 방법의 수행시간을 슬라이싱 시간을 포함하지 않고 분석해보자.

d. Sol1) 분석.
n개 중 최대값 찾기에서 n-1 개 최대값 찾기로 범위를 축소시켰으므로
T(n) = T(n-1) + c, T(1) = c > T(n) = cn, O(n) 이다.
이를 선형 재귀 호출 이라고 한다.

e. Sol2) 분석.
T(n) = 2T(n/2) + c, T(1) = c > T(n) <= 2cn = O(n) 이다.
이를 이진 재귀 호출 이라고 한다.

3. a^n 을 계산하기 (n을 양의 정수로 지정)

a. 선형 재귀로 작성.

def power1(a, n):
	if n == 1:
    	return a
    return a * power1(a, n-1) 

T(n) = T(n-1) +c = O(n)

b. 이중 재귀로 작성.

def power2(a, n):
	if n == 0: return 1
    if n%2 == 1:
    	return power2(a, n//2) * power2(a,n//2) * a 
    else: 
    	return power2(a, n//2) * power2(a,n//2) 

T(n) = 2T(n/2) + c = O(n)

c. 선형이지만 빠른 방법.

def power3(a, n):
	if n==0: return 1
    p = power3(a, n//2)
    if n%2 ==1: return p * p * a
    else: return p * p 

a, n 이 주어지면 이를 바탕으로 a, n//2 를 한 번 계산하여 p 에 저장. p 에 저장한 것을 짝수 홀수에 맞춰 재사용하므로 (각 2번씩) 이때의 추가 연산은 필요하지 않고 p의 재귀호출에만 시간이 투자된다. n > n/2 > n/2^2 > .. 1 하는데 총 logn 의 시간이 든다.

T(n) = T(n/2) + c = O(logn)

d. n이 임의의 정수일 때는? (음수일 수도 있다.)

def pow(a, n):
	if n < 0: return pow(1.0/a, -n)
    if n ==0 : return 1
    p = pow(a, n//2)
    if n%2 == 1: return p * p * a 
    else: return p * p 

4. BigMod 알고리즘

a^n 을 계산하는 분할정복 알고리즘을 a^n % m 을 계산하는 문제에도 적용해보자!

a. 굳이 매우 큰 수인 a^n 을 계산하고 나눌 필요가 없다.

b. (a b)%m = (a%m b%m) %m 이 성립한다. 이를 이용해서 % 연산을 재귀단계마다 적용할 수 있다.

def bigmod(a, n, m):
if n == 0: return 1
p = bigmod(a, n//2, m)
if n%2 == 0 : return (p p) % m
else: return (a%m p * p) % m

사실 각 재귀호출에 (p%m * p%m) %m 을 적용하면 더 좋을 거 같은데 그렇지 않는다. 일단 그렇다고 알고 있자.

6. 피보나치 수 구하는 5가지 방법

c. 분할 정복 방법1: 느려 ~

def fibonacci1(n):
	if n<=1: return n 
    return fibonacci1(n-1) + fibonacci1(n-2) 

지수시간이 걸림을 알아두자.

d. 분할 정복 방법 2: 빨라! > 잘 모르겠음. 무엇..?

우연히도 다음 행렬 계산의 값이 피보나치 수와 같다고 알아두자.

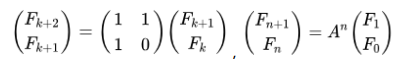
목표는 A^n 을 구하는 것이며, 이는 방금 전에 했던 O(logn) 알고리즘을 이용하면 된다.

def power(A, n):
	if n == 1: return A
    B = power(A, n//2) 
    if n%2 == 0: return mult_matrix(B, B)
    else: return mult_matrix(A, mult_matrix(B,B)) 
    

def fibonacci2(n):
	if n <= 1 : return n
    An = power([[1,1], [1,0]], n) 
    return An[1][0] 

O(logn) 이면 충분.

e. 분할 정복 방법 3:

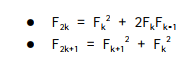
위 식을 이용한 풀이이다. 2k = k^2 + 2k(k-1) , 2k+1 = (k+1)^2 + k^2

def fibonacci3(n): 
	if n==0 or n==1: return n
    k = n//2 
    Fk = fibonacci3(k) #k 번째 항 
    Fk_minus_1 = fibonacci3(k-1) # k-1 번째 항 
    Fk_plus_1 = Fk_minus_1 + Fk # k+1 번째 항 = k번째 + k-1 번째
    if n%2 ==0: return Fk * Fk + 2 * Fk * Fk_minus_1 
    else: return Fk_plus_1 * Fk_plus_1 + Fk * Fk 

결국은 k-1 번째 항을 계산할 때와 k+1 번쨰 항을 계산할 때 각각 T(n/2) 번의 계산이 필요하므로
T(n) <= 2T(n/2) + c = O(n) 이다.

f. 선형 방법 4: 리스트를 이용한 방법
n개의 피보나치 수를 리스트에 담아 모두 계산하자.

def fibonacci4(n): 
	F = [0, 1]
    for i in range(2, n+1):
    	F.append(F[i-1] + F[i-2]) 
    return F[n] 

반복문 시간만 계산하면 되므로 O(n) 이다.

g. 선형 방법 5: 두 변수만 사용한 방법
리스트를 이용하지 않고 변수 두 개만 사용하자.

def fibonacci5(n): 
	a, b = 0, 1
    for i in range(2, n+1):
    	a, b = b, a + b 
    return b 

함수의 수행시간은 반복문만 계산하면 되므로 O(n) 이다.

7.

8. 예4: 하노이 탑

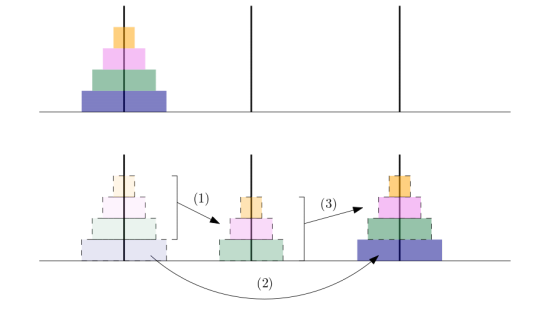
분할 : n-1 개와 가장 큰 1개로 분할 > 정복: n-1 개를 옮기는 문제를 2번 재귀적으로 해결.

• n-1 개를 먼저 가운데 막대로 옮김 T(n-1)
• 가장 큰 하나를 오른쪽으로: 1번
• 가운데 막대의 n-1 개를 오른쪽 막대로 옮김 T(n-1)
• T(n) = 2T(n-1) + 1
• O(2^n)

9. 예5: 이진 탐색

• 리스트 A 에 n개의 수가 저장되어 있다. 어떤 수 K가 A에 저장되어 있는지 알고 싶다. 최소 몇 번의 비교로 찾을 수 있을까?

• K 가 A 에 없는 경우에는 모든 수를 살펴봐야 하므로 n번의 비교는 반드시 필요하고, 이 경우가 최악이며, 동시에 반드시 필요함!

• 그러나 만약 A 의 수들이 오름차순 정렬된 상태라면 이를 이용해 탐색 범위를 반으로 줄이는 것이 가능하다.

재귀, 비재귀로 나뉘어 3가지 코드를 살펴볼 것이다.

g. Slicing + 재귀적으로 탐색

def binary_search(A, k):
	if len(A) < 1: return -1
    m = len(A) // 2 
    if A[m] > k: return binary_search(A[:m], k) 
    elif A[m] < k: return binary_search(A[m+1:], k) 
    else: return m

T(n) = T(n/2) + cn (cn 은 슬라이싱 때문에 그렇다.) = O(n)

h. Slicing X + 재귀적

def binary_search(A, l, r, k):
	if l > r: return -1
    m = (l+r) // 2
    if A[m] > k: return binary_search(A, l, m-1, k)
    elif A[m] < k: return binary_search(A, m+1, r, k)
    else: return m 

i. Slicing X + 비재귀적
슬라이싱 없고 비재귀적이라 가장 바람직한 이진탐색 코드, 통째로 외우자고 적혀있다.

def binary_search(A, K):
	l, r = 0, len(A)
    while l - r <= 0: 
    	m = (l+r)//2
        if A[m] > K: r = m-1 
        elif A[m] < K: l = m+1 
        else: return m 

10. 연속된 정수들의 합 중 최대가 되는 구간

a. 다음과 같은 방식으로 해결된다.

• 모든 인덱스 쌍 i, j 에 대해 A[i] 부터 A[j] 까지의 합을 계산, 조합에 O(n^2), 계산에 O(n) 총 O(n^3)

• prefix 합 P[i] 계산 후 P[j] - P[i-1] 을 계산. 이 중 최대 합이 되는 구간 선택. 각 prefix 합에는 O(n) 시간이 걸리며 모든 쌍에 대한 계산은 O(n) 걸림. 총 O(n^2)

• O(nlogn): 분할정복 방법으로

• O(n): DP 로 해결

b. 아이디어
최대구간이 위치한 경우를 다음과 같이 나눠보자.

• L에 있는 경우, R에 있는 경우, 걸쳐 있는 경우
• L또는 R에 있는 경우는 재귀적으로 구할 수 있다.
• 걸쳐 있는 경우는 L의 가장 끝수와 R의 가장 첫 수를 포함한다는 것이다. L의 가장 끝 수부터 왼쪽으로 합을 구하면서 가장 큰 구간을 찾고, R의 첫 수부터 오른쪽으로 합을 구하면서 큰 구간을 찾아 구간을 연결하자.

T(n) = 2T(n/2) + cn = O(nlogn)

11. 봉우리 찾기

a. 1차원인 경우
리스트 A에 n개의 서로 다른 양의 정수가 있다고 하자. A[i] 가 i지점의 높이를 의미하며, 높이 A[i] 가 양 옆의 높이보다 높다면 봉우리가 된다. A[0]은 왼쪽 위치를 고려하지 않아도 좋고, A[n-1] 은 오른쪽 위치를 고려하지 않아도 좋다. 주어진 리스트 A에 봉우리가 있다면 봉우리 하나를 찾아 출력하자.

• A에 봉우리가 없을 수도 있나? 서로 다른 양의 정수이므로 최대값은 무조건 봉우리이다
• A[0] 부터 봉우리인지 차례로 검사할 수 있다. O(n) 시간이 걸린다
• 이진 탐색이 가능할까? A[k-1] > A[k] 라면, A[0] ... A[k-1] 중에 하나 이상의 봉우리가 존재한다. 왼쪽으로 진행하며 내려간다면 그것이 봉우리이고, 내려가지 않아도 A[0] 가 봉우리
• 반대로 A[k-1] < A[k] 이면 A[k] ... A[n-1] 중에 봉우리가 하나 이상 존재.
• 따라서 반씩 쪼개서 찾을 수 있으므로 일의 양은 반으로 줄어들고, 한 번 비교하여 왼/오른쪽을 선택하는데는 c의 시간만 든다. T(n) = T(n/2) + c = O(n) 이다.

b. 2차원 버전
2차원 리스트 A에 서로 다른 양의 정수가 저장되어 있다. A[i][j] 가 봉우리이기 위해선 동, 서, 남, 북 모두보다 커야한다. 2차원 봉우리가 존재한다면 하나를 찾아 출력하자.

• A에는 하나 이상의 봉우리가 존재하나? 그렇다. 무조건 최댓값은 봉우리이다.
• 값을 하나씩 살펴본다면 O(n * m) 의 시간이 필요
• 열에서 봉우리를 찾고, 행에서 찾는 방법은 적절하지 않다.
• m/2번쨰 열에서 최대값을 찾자. (일단 열에서 1차원 봉우리이다.) 해당 최대값의 좌우를 비교해 오른쪽이 크다면 봉우리는 오른쪽에, 왼쪽이 크다면 봉우리는 왼쪽에 있음을 확신한다.

n n 의 2차원에서 봉우리를 찾는 시간을 T(n) 이라 할때,
T(n) = n(열) + n(행) + T(n/2) 이다. 한 번 수행할 때 n/2 n/2 의 문제로 바꿔놓는다!

T(n) = T(n/2) + cn = O(n) 이다.

14. 큰 수 곱셈

이런식으로 계산하면 n자리 수의 곱셈을 n//2 자리 수의 곱셈 4개로 쪼개는 것으로
T(n) = 4T(n/2) + cn = O(n^2) 이다. 자른 의미가 없는데..?

이때 Karatsuba 가 제시한 빠른 방법을 사용하면 된다.
Karatsuba 알고리즘은 n/2 자리수 곱셈 3개로 분할한다!

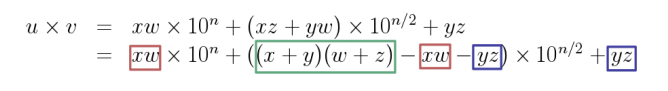
위의 식에서 xw, yz 는 n/2 인 식이며, x+y * w+z 는 n/2 + 1 인 식이므로
T(n) = 2T(n/2) + T(n/2 + 1) + cn
따라서 3T(n/2) + cn 으로 계산해도 괜찮다. 공식에 따라 n^log23 으로 나온다.

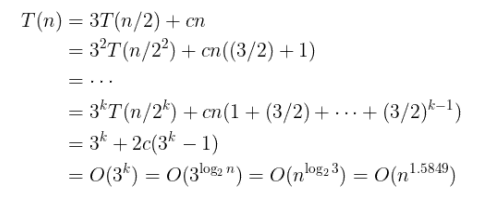
15. 이차원 행렬 곱셈

위의 문제를 2차원으로 확장하면 이차원 행렬의 곱셈 문제가 된다.

• 학교식 계산에 따르면 두 수의 덧셈, 곱셈 연산을 O(n^3) 해야함
• Karatsuba 알고리즘처럼 A, B 각각을 n/2 * n/2 부행렬로 나눠 중복 곱셈을 피하면서 계산한다.
• 8개가 아닌 7개의 n/2 * n/2 로 계산하는 게 가능해졌다. T(n) + 7T(n/2) + cn^2 = O(n^log27)

16. 원주율 정확하게 계산

• 배열에 자리수를 나눠 저장
• 4자리씩 나눠 저장
• 뒤에서 리스트 거꾸로 불러오며 연산