[HUFS/Algorithm] 5. Sorting (정렬)

1. Sorting 정의

리스트에 저장된 값들을 크기 순서에 따라 재배열하는 문제.
비교횟수와 자리바꿈 횟수를 최소로 하는 것이 목표.

2. Python 제공 정렬함수

python 에서 제공하는 정렬함수는 Tim sort 이다.

a.sort() 또는 b = sorted(a) 를 이용하자.

3. 정렬 알고리즘 분류

a. 기본 정렬 알고리즘(단순하지만 느림) : insertion, selection, bubble

b. 빠른 정렬 알고리즘(복잡하지만 빠름) : quick, heap, merge

c. 특별한 상황 : count, radix, bucket

정렬 알고리즘의 성질 2가지

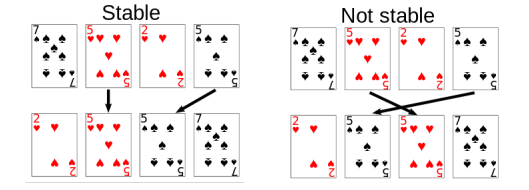
Stable vs unstable
크기가 같은 숫자인 경우, 입력 순서를 정렬 후에도 유지하는 알고리즘을 stable 하다고 한다.

in-place vs not-in-place
상수 개의 추가 변수만 사용한 알고리즘을 inplace 하다고 함.

5. 기본정렬 알고리즘 3가지

a. 느리지만 간단한 정렬 알고리즘: insertion, selection, bubble

b. 세 알고리즘 모두 공통적으로 n-1 번의 round 를 거치고, round 마다 하나의 수를 정렬하는 방식이다. (나머지 하나의 수는 자동으로 정렬)

• insertion : 왼쪽부터 점진적으로 정렬
• selection : 가장 큰 값부터 차례대로 찾기
• bubble: 가장 큰 값부터 차례대로 찾기

c. Insertion sort 알고리즘

def insertion_sort(A, n):
	for i in range(1, n):
    	j = i - 1
        while j >= 0 and A[j] > A[j+1]:
        	A[j], A[j+1] = A[j+1], A[j] 
            j = j - 1 

d. Selection sort 알고리즘

def selection_sort(A, n):
	for i in range(n-1, 0, -1):
    	m = get_max_index(A, i)
        A[i], A[m] = A[m], A[i] 


def get_max_index(A, i):
	m, m_index = A[0], 0
    for j in range(1, i+1):
    	if m < A[j]:
        	m, m_index = A[j], j
    return m_index 

반복문을 돌며 큰 수를 차례대로 찾는다. 큰 수를 찾고 인덱스 m을 반환해오면, 그 수를 자리교환해 가장 뒤, 그 다음 뒤로 보내는 구조!

e. Bubble sort 알고리즘

def bubble_sort(A, n):
	for i in range(n):
    	for j in range(1, n):
        	if A[j-1] > A[j]:
            	A[j-1], A[j] = A[j], A[j-1]

g. 이진탐색을 이용한 insertion 정렬 알고리즘

자신의 왼쪽 정렬된 부분에서 위치를 찾아 insert 하는 과정을 이진탐색을 이용하자.
A[i] 는 insert 를 기다리는 숫자이다.

만약 A[j] = 2 A[j+1] = 7 A[i] = 5 라면 A[j+1] 부터 A[i-1] 까지 오른쪽으로 한 칸씩 이동하시고 (n) A[i] 가 [j+1] 로 이동하면 된다.

비교횟수를 Big-O? : insert 하기위한 비교횟수는 O(logi) 이다. (정렬된 값들 중 자신의 위치) 모든 i들에 대해 계산해야 하므로 O(nlogn) 이라 하자.

이동횟수를 Big-O? : 삽입될 위치가 가장 왼쪽이라면 매번 n-1 개의 값이 이동해야 한다. 따라서 O(n^2)

따라서 O(nlogn) + O(n^2) = O(n^2)

h. 수행시간, stable, inplace 여부를 정리하자!
insertion: n^2, stable, inplace
selection: n^2, not stable, inplace
bubble: n^2, stable, inplace

6. Quick sort 알고리즘

a. 실제 구현에서 가장 빠른 정렬 알고리즘 중 하나

b. 분할 정복 알고리즘의 예 중 하나

c. Quick select 알고리즘과 매우 유사.
피봇보다 작은 값들을 리스트의 왼쪽, 큰 값들을 오른쪽으로 재배열 한 후, 양쪽을 재귀적으로 다시 정렬

d. 아이디어: quick_sort(A, first, last) # first 부터 last 까지 정렬하는 함수

• first >= last 인 경우는 정렬할 값이 1개 이하이므로 리턴
• first < last 인 경우는 피봇 지정, 시작.
• pivot = A[first] (가장 왼쪽의 값을 피봇으로)
• 피봇보다 작은 값들은 왼, 큰 값들은 오른쪽에 오도록 배치 후
• 각각 재귀호출

e. 구현방법1: 리스트 A에서 pivot 을 기준으로 나누는 첫번째 방법 (inplace, unstable)

def quick_sort(A, first, last):
	if first >= last: return 
    left, right = first+1, last
    pivot = A[first]
    while left <= right:
    	while left <= last and A[left] < pivot:
        	left += 1
        while right > first and A[right] > pivot:
        	right -= 1 
        if left <= right:
        	A[left], A[right] = A[right], A[left]
            left += 1 
            right -= 1 
    A[first], A[right] = A[right], A[first] 
    quick_sort(A, fisrt, right-1)
    quick_sort(A, right+1, last) 

시작은 첫 번째 값을 피봇으로 정하고 부터이다. left<= right 인 한 계속해서 진행되고, 왼쪽 인덱스가 이동하면서 피봇보다 큰 값을 찾는다. 오른쪽 인덱스는 왼쪽으로 오면서 피봇보다 작은 값을 찾는다. 그러면

피봇(중간값) , 피봇보다 큰 값 , 피봇보다 작은 값을 찾게되고
피봇보다 작은 값, 피봇보다 큰 값으로 교체해주고 인덱스는 이동해주며
피봇보다 작은 값, 피봇, 피봇보다 큰 값으로 한 번 더 바꿔준다.

f. 구현방법2: 리스트 A에서 pivot을 기준으로 나누는 두 번째 방법 (in-place/unstable)

def quick_sort(A, first, last): #first부터 last 제시된 범위를 quick sort
	if first >= last: return 
    smaller, equal, larger = first, first, last+1
    pivot = A[first]
    while equal < larger:
    	# A[equal] 은 우리가 현재 바라보고 있는 값이다
        if A[equal] < pivot:
        	A[smaller], A[equal] = A[equal], A[smaller]
            smaller, equal = smaller+1, equal+1
        elif A[equal] == pivot:
        	equal += 1 
        else: 
        	larger -=1 
            A[equal], A[larger] = A[larger], A[equal] 
    quick_sort(A, first, smaller-1)
    quick_sort(A, larger, last) 

g. 구현방법3: 새로운 리스트를 추가로 사용 (not-in-place/stable)

def quick_sort(A):
	if len(A) <= 1: return A
    pivot = A[0] 
    S, M, L = [], [], []
    for x in A:
    	if x < pivot: S.append(x)
        elif x > pivot: L.append(x)
        else: M.append(x)
    return quick_sort(S) + M + quick_sort(L) 

j. 수행시간

• 좋은 시나리오: n/2개, n/2 개로 분할되는 경우 >> T(n) = 2T(n/2) + cn = O(nlogn)
• 가장 나쁜 시나리오 >> T(n) = T(n-1) + cn = O(n^2)

평균적인 수행시간도 O(nlogn) 이어서 느리지 않다.

l. 점화식으로 평균 수행 시간 계산하기 (멱급수 이용)

7. Merge sort 알고리즘

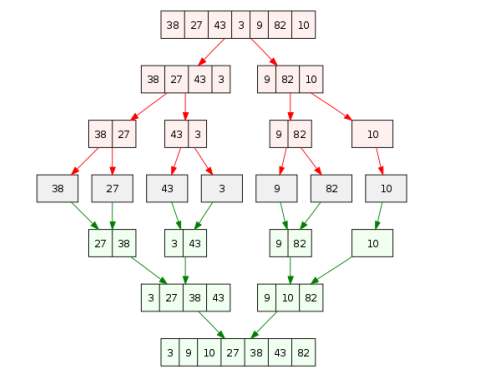
a. 전형적인 분할 정복 알고리즘 중 하나

b. 최악의 경우에도 O(nlogn) 에 동작하는 최적 정렬 알고리즘 중 하나.
(quick_sort 가 분할된 크기가 비슷하지 않아 재귀를 많이 하게되어 문제라면, 그냥 강제로 반씩 분할하면 되지 않나?)

c. 코드
def merge_sort(A, first, last):
if first >= last: return
merge_sort(A, first, (first+last)//2)
merge_sort(A, (first+last)//2+1, last)
merge_two_sorted_lists(A, first, last)

정렬된 것들 중 하나씩 비교하며 작은 것을 가져오는 것과 같다. (가위바위보해서 지면 들어가는 것, 팀게임!) 끝 부분 반복문 2개는 먼저 리스트 하나가 끝나면 나머지는 못돌아서 나머지를 돌려주는 것이다. 마지막 반복문은 B에 담은 것을 A로 옮기는 반복문이다.

d. 분할: 숫자 하나가 될 때까지 반씩 분할
정복: 다시 정렬된 두 리스트를 합병해 올라간다

f,g: stable, not in-place

h. T(n) = 2T(n/2) + cn = O(nlogn)

i.

j. merge 정렬 방식 응용 1: 입력 리스트 숫자들에 대한 inversion 개수 세기

• A[2,4,1,3,5] 라면 (2,1), (4,1), (4,3) 의 숫자가 서로 역전되어 있으므로 inversion(A) = 3 이다.

방법1) 가장 단순한 알고리즘은 모든 쌍 (a,b) 를 보면서 a>b 인지 검사하는 것이고, O(n^2) 이다. (너무 느려 ~)

방법2) nlogn 에 해보자. (merge sort 진행하면서 inversion 을 세면 된다!)

• merge sort 하여 한 번 반으로 나눈다
• 반으로 나눈 상태에서 왼쪽 반의 inversion 개수는 L, 오른쪽 반의 개수는 R 이라고 하자
• 나중에 왼쪽 반, 오른쪽 반을 각각 정렬하고 전체 병합을 하면서 오른쪽 반의 요소가 들어가면 들어가지 않은 왼쪽 반의 요소가 모두 inversion 이다. (병합하면서 센다.)
• 따라서 inversion 개수세기도 그냥 merge sort 의 수행시간과 같은 O(nlogn)이다.
  

8. Heap sort 알고리즘

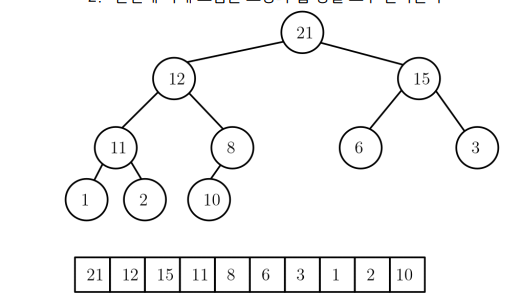
a. Heap : 다음 성질을 만족하는 리스트에 저장된 값의 시퀀스이다.

• 이진트리여야 한다(마지막 레벨을 제외한 각 레벨의 노드는 모두 채워져있어야 한다 / 마지막 레벨에선 왼쪽부터 채운다)

• 자식노드의 값은 부모노드 값보다 크면 안된다.
  

• 힙 성질에 따라 루트 노드에는 가장 큰 값이 와야 한다(max)

• 힙의 높이 h = O(logn)

• 힙 성질을 만족하지 않으면, 값을 재배열하여 힙을 만든다. (make_heap, heapify_down)

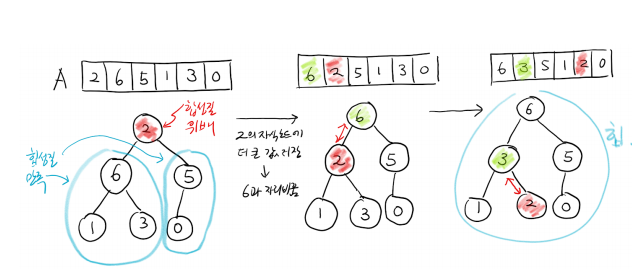
• heapify_down(k) 함수
  A[k] 의 자손들은 모두 힙 성질을 만족시킬 때, A[k] 를 아래로 내려가면서 맞는 위치로 이동시키는 함수이다. (내려가는데 O(logn) 의 시간이 걸린다.)
  

def heapify_down(self, k, n):
	# n은 힙의 전체 노드 수를 말한다. 
	while 2 * k+1 < n:
    	L, R = 2 * k+1, 2 * k+2 
        if L < n and self.A[L] > self.A[k]: #왼쪽 자식과 비교
        	m = L
        else:
        	m = k
        if R < n and self.A[R] > self.A[m]: #바꾼 수와 오른쪽 자식 비교
        	m = R 
        if m! = k: 
        	self.A[k], self.A[m] = self.A[m], self.A[k] 
            k = m # 내려온 값이 m이므로 이제 m=3 이 새로운 k가 됨. 다시 비교.
        else: break  # 이미 정렬이 완료되어 있었음. 

• make_heap 함수: 현재 리스트의 전체 값들을 힙 성질을 만족하도록 배열.

def make_heap(self):
	n = len(slef.A)
    for k in range(n-1, -1, -1):
    	self.heapify_down(k, n)

heapify_down 은 마지막 노드부터 0번까지 앞으로 진행시킨다. 함수 한 번 실행에 O(logn) 이고, n 번 실행하니, O(nlogn) 이다!

• heap_sort() 함수
  make_heap 과 heapify_down 을 반복적용하여 오름차순으로 배치하는 함수이다. 힙 정렬 알고리즘이라 불린다!
  원래 힙에서는 가장 큰 값이 루트에 저장되어 있지만 정렬을 위해서는 가장 마지막에 위치해야 한다. 이를 위해
  
  다시말해, 마지막 노드부터 큰 값으로 하나씩 정렬해나가는 방식이다.

def heap_sort():
	n = len(self.A)
    for k in range(len(self.A)-1, -1, -1):
    	self.A[0], self.A[k] = self.A[k], self.A[0] 
        n = n-1 
        self.heapify_down(0, n) 

1. 가장 큰 값인 루트노드와 맨 뒤 swap (n번 수행)
2. 올라간 값을 heapify_down (logn)
   따라서 O(nlogn) 이다.

• heapify_up 함수
  기존의 힙에 새로운 값을 삽입하는 연산이다. 새로운 값은 리프에 위치하므로, 올라가면서 자신의 위치를 찾아야 한다. A[(k-1)//2] 는 어렵게 생각하지 말자. 해당 노드가 k일 때 부모 노드의 인덱스이다!

def heapify_up(self, k)
	while k>0 and self.A[(k-1)//2] < self.A[k]:
    	self.A[k], self.A[(k-1)//2] = self.A[(k-1_//2], self.A[k]
        k = (k-1)//2 
def insert(self, key):
	self.A.append(key)
    self.heapify_up(len(self.A)-1) 

그냥 올라가면 되므로 down 과 마찬가지로 O(logn) 시간이 걸린다.

• 힙에서 Search 는 O(n), deleteMax 는 O(logn) 이다.

9. 비교횟수의 하한? (증명하라)

10. 하한증명

11. Radix sort 알고리즘

비비교기반 알고리즘으로, 자릿값을 보고 정렬하는 알고리즘이다.

자리수가 최대 d인 정수 n개를 정렬한다고 하자.

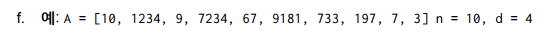
1. A[0] 부터 1의 자리 값만 보고 큐에 넣는다.
   

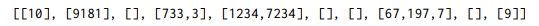
2. 0번째 큐부터 dequeue 해서 모은다. (1의 자리 수에 의해 정렬된 상태 완성)
   

3. 10의 자리 값만 보고 해당되는 큐에 넣는다.
   

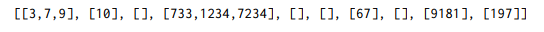
4. 다시 dequeue 해서 모은다. 그러면 10의 자리와 1의 자리 값에 따라 오름차순으로 정렬된 상태가 된다.
   

5. 100의 자리, 1000의 자리에 대해 반복.

• 수행시간은?
  인큐, 디큐는 각각 O(1) 의 시간이 든다. 자리수가 d개라면, 모든 수 n개에 대해서 d번 해당 연산을 수행하기에 O(dn) 이다. 비비교기반 알고리즘의 경우 두 수의 비교가 필요 없어 정렬 문제의 하한을 적용할 수 없다. 만약 d가 상수 값이라면 O(n) 에 수행됨!

참고하자.

정렬을 이용한 문제풀이

1. Uniqueness problem : n 개의 값이 모두 다르면 YES, 같은 값들이 있으면 No 을 출력

방법1) 이중 for 루프를 반복하면서 일일히 비교 > O(n^2) 너무 느려 ~
방법2) 오름차순 정렬 후 (heap, merge sort) 둘 씩 비교.
O(nlogn) + O(n) = O(nlogn) 은 워스트 케이스, 만약 linear scan 한다면 O(n) ?
방법3) Hash Table: 평균 O(n)

for x in A:
	if H.serach(x) != None: x  #만약 해시테이블에 있다면 
    else: H.set(x) # 없다면 .set 
    return True  

하한은 nlogn 이다. ㅋ

2. Pair sum
주어진 리스트 [-3, 6, 1, 7, 2, 5, -4] 가 있을 때 합이 8인 쌍을 구하는 문제

1. 모든 쌍을 돌며 합이 k가 되는 지 확인하는 O(n^2)

2. 정렬하여 다루는 방법
   [-4, -3, 1, 3, 5, 6, 7] >> 정렬하는데 O(nlogn) 이 걸린다.
   가장 왼쪽 인덱스 i, 오른쪽 j
   양 끝 수를 더하며 값이 8보다 작으면 i += 1 , 같으면 i += 1, j -= 1, 크면 j -= 1 한다. O(n)
   총 O(nlogn)

3. Hash Table : 평균 O(n)

for x in A:
	H.set(x) # 모두 집어넣는다: O(n) 
for x in A:
	if H.search(k-x) != None: print(x, k-x) # k-x, 즉 x 의 짝이 있는지 찾고 있으면 출력. O(n) 

평균이 O(n)

3. 세 수의 합이 0인지
위의 문제를 변형시켜 a+b = -c 가 되는 페어를 찾으면 된다.

A.sort() 로 정렬한다. >> O(nlogn)
반복문을 돌며 모든 요소에 대해 합이 -c 가 되는 페어가 있으면 출력한다. >> 모든 요소들에 대해 n, 합이 -c 인 것을 찾는 것이 위의 n >> O(n^2)

합으로 연결되어 총 O(n^2)