[HUFS/Algorithm] 6. DP

Fibonacci 수 계산

1. 재귀 알고리즘

재귀적으로 중복 호출되어 매우 느리게 실행된다. (지수 시간이 필요)
따라서 피보나치 수를 계산 후 기록해놓고 - 필요할 때 재사용하자는 아이디어를 제시한 것!

2. 기록 + 재사용 재귀 알고리즘(memoization)

def fibo(n):
	if n in memo.keys():
    	return memo[n]
    if n<=1:
    	f = n
    else:
    	f = fibo(n-1) + fibo(n-2) 
    memo[n] = f 
    return f 

fibo(k) 값은 처음 게산이 되었을 때 저장, 나중엔 재사용된다.
이때의 수행시간은 O(n)

3. 기록 + 재사용 비재귀 알고리즘

def fibo(n):
	F = [0,1]
    if k in range(2, n+1):
    	F.append(F[k-1] + F[k]) 
    return F[n] 

이때의 수행시간도 역시 O(n) 이다.

DP, 동적계획법

원래 문제를 작은 문제로 분할하여 분할된 문제의 해답을 기록해 놓은 후, 더 큰 문제의 해답을 계산할 때 재사용 하는 방법을 의미한다.

계단 오르는 경우의 수

1. 부문제를 정의: 거꾸로 정의하면 되지 않을까? 바로 한 층 전에는? n-1 층이나 n-2 층에서 왔을 것이다.

2. 원문제의 해를 부문제의 해의 식으로 표현

3. DP 테이블
   C[n] = C[n-2] + C[n-1]
   C = [1,1]
   for k in range(2, n+1): C[k] = C[k-1] + C[k-2]

d. 올바르냐?

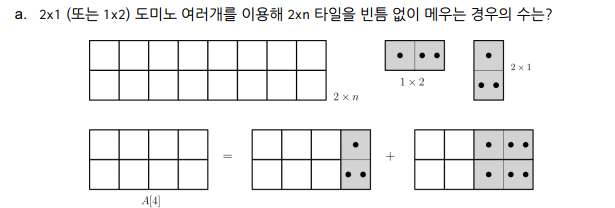
도미노 타일링