[Interest] Gamma, Beta, Normal distribution

(본 포스팅은 2023-1 성균관대 수학교육과 확률통계학1의 수업 중 감마, 베타, 정규분포를 다룬 강의를 정리한 것입니다. 강의 내용과 필기한 피피티의 저작권 모두 이에 있습니다.)

Gamma distribution

이러한 감마분포는 어떤 사건이 일어나기까지의 시간을 계산하는데 주로 쓰인다. (수명, 고장시간, 서비스시간, 대기시간 등)

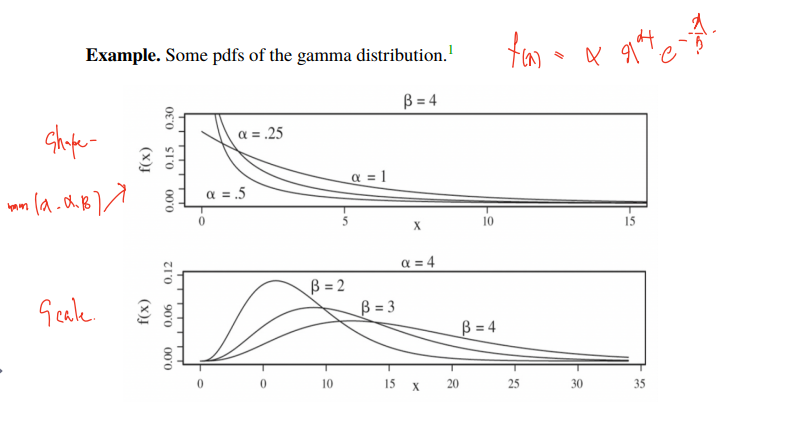
• 알파는 shape, 베타는 scale 을 결정하는 parameter 다.

mgf of Gamma.

mgf 를 통해 계산한 평균과 분산은

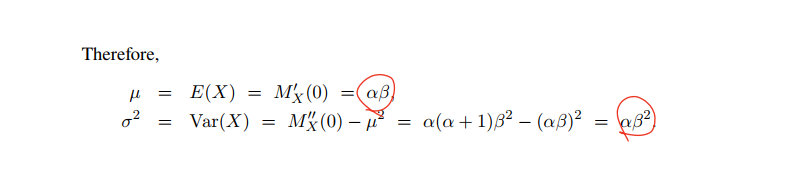
Special case (지수분포, 카이제곱 분포)

• Gamma(1, 베타) 는 exponential distribution with parameter 베타와 같다.
• 제곱의 분포는 카이제곱(1)이다.
• 제곱의 합의 분포는 카이제곱(r) 파라미터 분포이다.
• Additivity에서 1과 3.3.1 을 이용해 2를 계산할 수 있음을 보인다.

Beta distribution

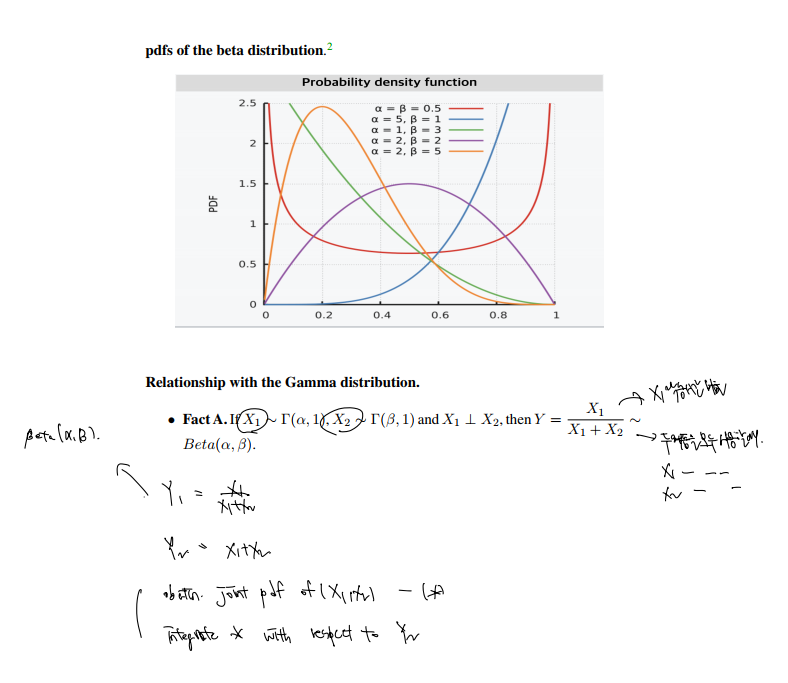
Mean and variance of Beta distribution Proof.

Dirichlet distribution

The Normal Distribution

Standard normal distribution

mgf and moments of N(0,1).

Normal distribution.

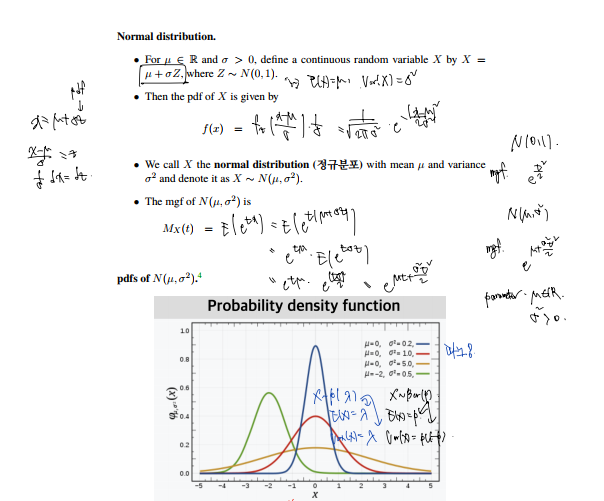
Properties.

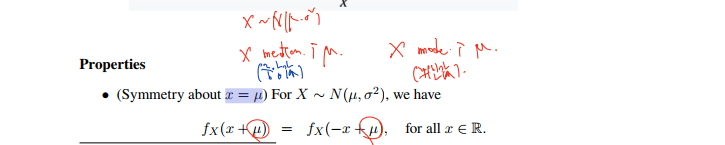
표준정규분포를 따르는 확률변수 x^2 은 카이제곱(1)임을 증명.