[Linear algebra] 내적공간 (2)

[Linear algebra] 내적공간 (2)

이번 포스팅에서는 지난 포스팅에서 배웠던 orthogonal, orthonormal 을 활용하여, 일반적인 basis 또는 basis subset 가 주어졌을 때 orthonormal basis 를 찾는 방법을 알아볼 것이다. 이를 위해, 우선 orthonormal basis 가 무엇인지 알아보고, 그다음 Gram-Schmidt process 라 불리는, 구체적으로 orthonormal basis 를 만드는 과저을 알아보자.

1. Orthonormal basis

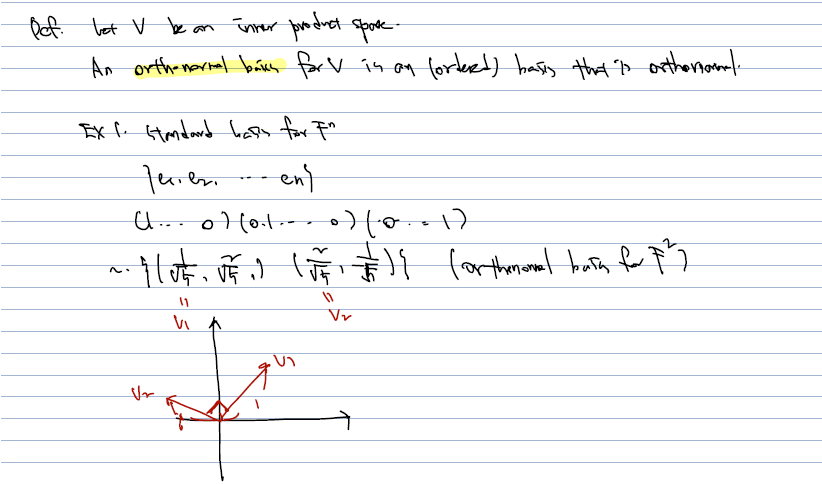
Orthonormal basis 는, 말그대로 orthonormal 한 기저를 뜻하는데, 아래의 예시를 보면 쉽다.

• F^n에 대한 일반적인 standard basis 는 {e1, e2, ..., en} 인데, 이는 그 자체로 1. 기저이고, 2. orthonormal (각 벡터끼리 곱하면 0, 크기가 1) 하기 때문이다.

• F^2에서 주어진 두 벡터도 orthonormal basis 이다.

우리가 배운 개념인 orthogonal 또는 orthonnormal subset 을 활용해, 이들이 span 하는 공간 안에 있는 임의의 벡터 y 를 표현하는 방법을 알아보자.

1. orthogonal subset 을 가지고 y를 표현할 경우.

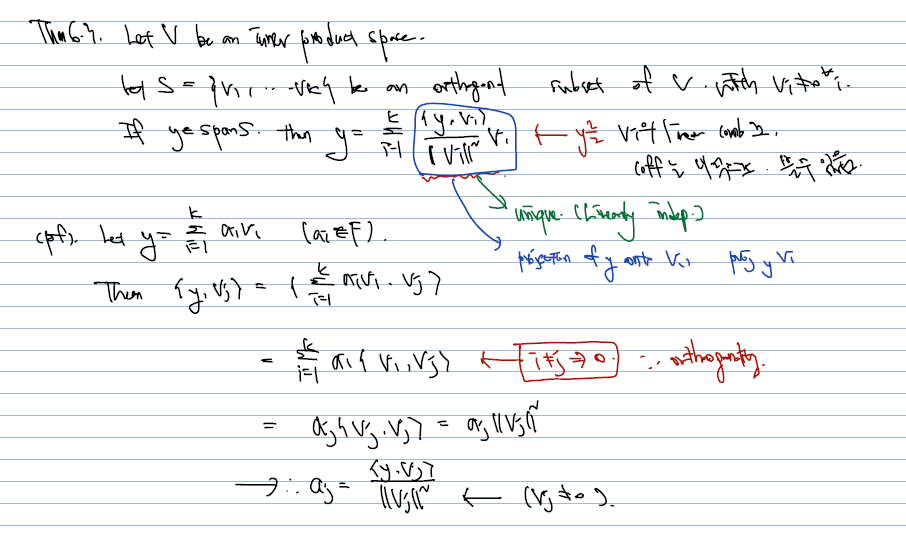
• y는 vi 들의 linear combination 으로 표현될 수 있음을 기억한다면, 앞에 계수들이 내적으로 주어진다는 것 외에는 특별할 것이 없다.
• 계수들이 정확히 <y, vi> 를 vi 크기의 제곱으로 나눈다는 것의 증명은 어렵지 않다. y를 일반적인 vi들의 linear combination 으로 표현한다 가정했을 때, 이들이 꺼내어 쓰여질 수 있고, 이때의 계수들이 내적을 포함한다는 것만 보여주면 된다.

2. Orthonormal subset 을 가지고 y를 표현할 경우. (vi 크기의 제곱이 1으로 확정!)

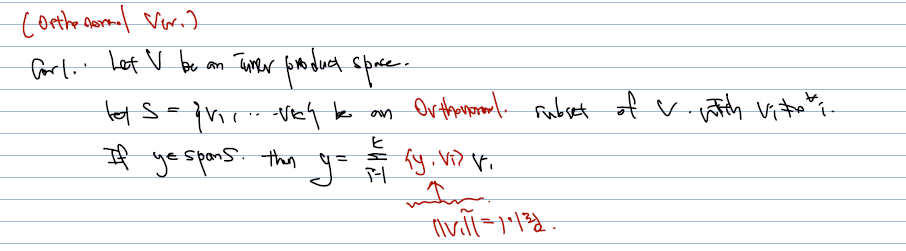
orthonormal basis 에 대한 예시 몇 가지를 보자.

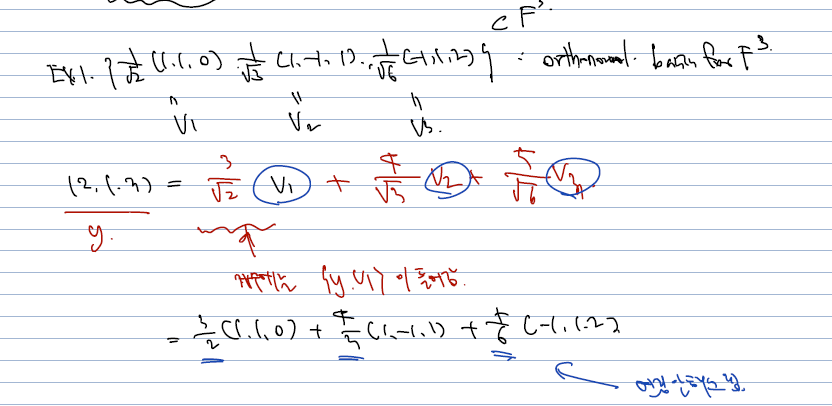
• 이 orthonormal basis 는 각 성분끼리 내적하면 0이 뜨고, 크기는 모두 1인 basis 가 된다.
• 이때 (2, 1, 3) 을 이 basis 로 표현하고자 한다면, 단순히 <y, vi> 을 내적한 것을 vi의 계수로 써주기만 하면 된다.

다음의 목표는, inner product space 자체에서 그렇다면 어떻게 orthonormal basis 를 찾느냐 하는 것이다. 여기까지 왔다면 orthonormal basis 를 찾는 일반적인 정리된 과정이 있으면 좋겠다는 생각을 자연스레 할 수 있게 되는데, Gram-Schmit 과정이 바로 그것이다!

2. Gram-Schmidt process (그람-슈미트 과정)

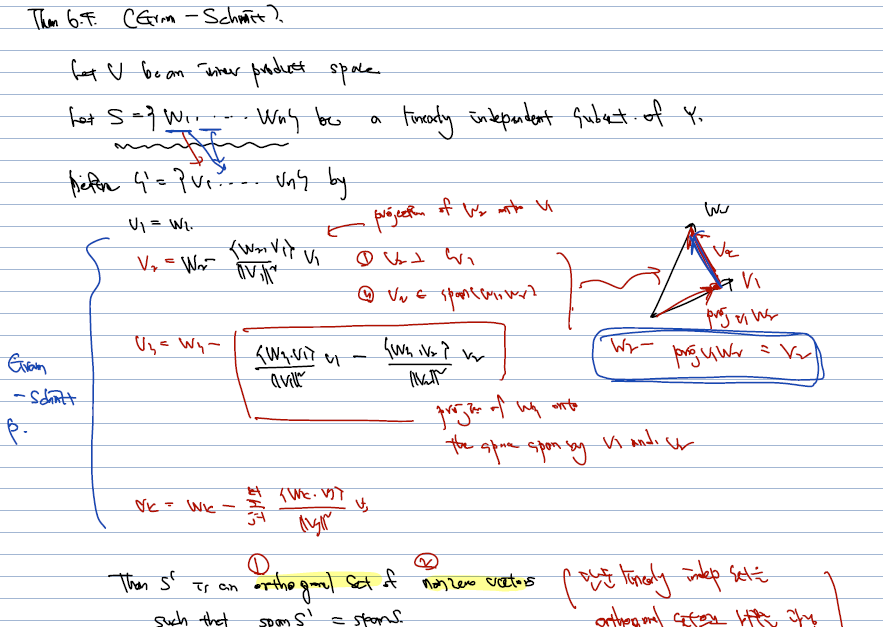
inner product space 가 주어진 vector space V 위에서, y를 표현할 수 있는 linearly independent subset 이 이미 주어졌을 때, 이걸 가지고 각각 orthogonal 하게, 크기가 1이도록 하는 subset 을 찾는 방법은 다음과 같다.

linearly indep subset 이 S = {w1, w2, w3, ..., wn} 이고, 만드려고 하는 orthonormal subset S' = {v1, ... vn} 이라고 하면,

1. v1 = w1 로 준다.
2. v2 부터는 v1과 orthogonal 해야 하고, w2 가 있을 때 정확히 v1 로 정사영(projection) 한 벡터를 뺌으로써 이를 구할 수 있다. 따라서, w2 에서 v1을 빼는데, w2를 v1에 대해 정확히 정사영한 크기를 맞춰주기 위해 <w2, v1>/||v1||^2 식이 들어가게 된다.
3. 마찬가지로 v3 는 v1, v2 와 모두 직교해야 하면서, w3 를 기준으로 w3을 v1에도 정사영한 것을 상수배, v2에도 정사영한 것을 상수배를 각각 해준 것을 빼게 된다. 그럼 말 그대로 w3에서 v1과 v2 방향에 해당하는 직교 성분을 없앨 수 있게 된다.
4. 일반적으로는 v_k 는 w_k에서 각 <wk, vj> 를 내적해준 것을 vj 에 계수로 하여 제외해주면 된다. 더 직관적으로는, w_k를 추가하고 싶은데, 추가할 때 이미 나온 vj 들과 직교를 이뤄야 하므로, 각각의 방향에서 정사영한 성분들을 제외해주면 되는 것이다.

이런 그람슈미트 과정을 거쳐 만든 subset S' 는 1. orthogonal set 이 되며, 2. nonzero vectors s.t. spanS' = spanS 가 된다. 즉, 처음 가지고 있던 set 이나 orthogonal 하게 만든 set 이나 span 하는 공간 자체에는 차이가 없다. 그저 성분들이 직교하도록 만들어준 것일 뿐.

(Gram-Schmidt process 예시)

실제 예시를 보며 orthogonal subset 을 만들어보도록 하자.

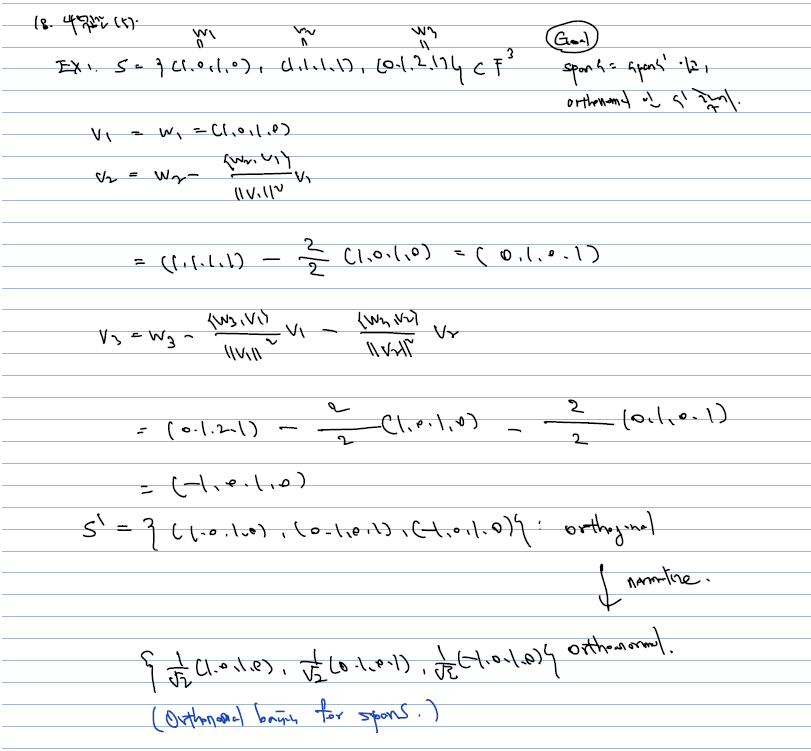
• 새롭게 얻은 {(1, 0, 1, 0), (0, 1, 0, 1), (-1, 0, 1, 0)}은 orthogonal subset 이 되며, 이를 norm 으로 나눠주기만 하면 orthonormal subset 이 된다. 이 경우, 모든 성분이 linearly indep 하고, V의 차원 자체가 3이므로 orthonormal basis 가 된다.

이걸 가지고, V의 임의의 원소 x를 orthonormal basis 로 표현한다는 theorem 을 얻을 수 있고, 역시나 linear combination 의 계수는 내적으로 간편하게 주어짐을 알 수 있다.

여기까지가 되었다면 orthonormal complement 에 대해 학습할 수 있는 상태가 되는 것이다.

3. Orthogonal Complement

Inner product space V의 부분집합 S에 대해 S의 orthogonal complement 는 다음과 같다.

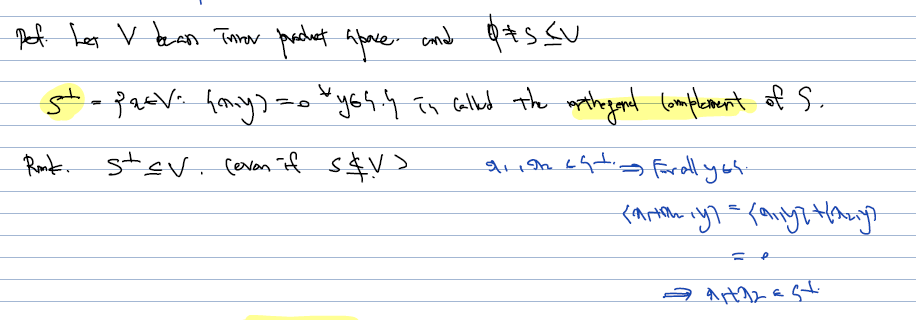
S의 orthogonal complement 란, S의 임의의 원소 y를 아무거나 가져와서 x와 내적했을 때 0이 되는 x 원소들을 모아둔 부분 집합을 말한다. 즉, S 자체와 orthogonal 함을 이루는 subspace 를 orthogonal complement 라 하고, S perpendicular 이라 하여 S perp 로 표시하게 된다.

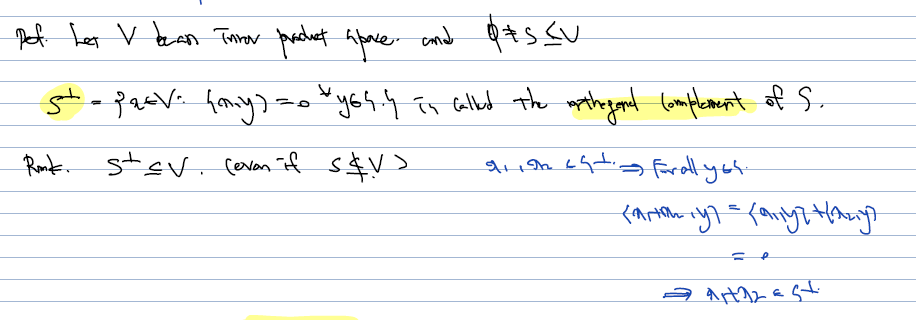
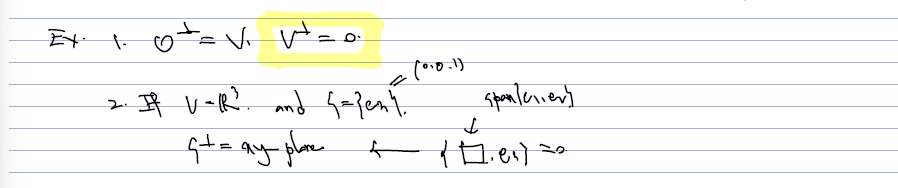
• 예컨대 0은 V 내의 모든 원소와 내적해도 0이 나오므로 0의 orthogonal complement 는 V, 마찬가지로 V의 orthogonal complement 는 0 이 된다.

• V = R^3 인데, S = {e3} 이라면 S의 orthogonal complement 는 xy-plane 상의 임의의 원소를 가져와서 e3 과 내적하면 무조건 0 이므로 xy-plane 이 된다.

아래의 theorem 은 이 orthogonal complement 와 원래 집합의 direct sum 이 inner product space V를 이룬다는 것. 즉, V는 finite dimensional subspace W와, 이 subspace 의 orthogonal complement 로 이루어진다는 직관이 된다.

이는 다른 말로, V의 원소 y는 W의 원소 u 와 W의 orthogonal complement에서 가져온 원소 z의 합, 즉 y = u+z 가 성립하는 경우와 마찬가지 명제가 된다.

이때, u의 기하적 의미를 챙겨둘 필요가 있다. W 위에 놓인 u의 경우, y-u = z로 표시해서 이해하면, W 위의 벡터들 중 가장 y와 가까운 벡터가 된다.

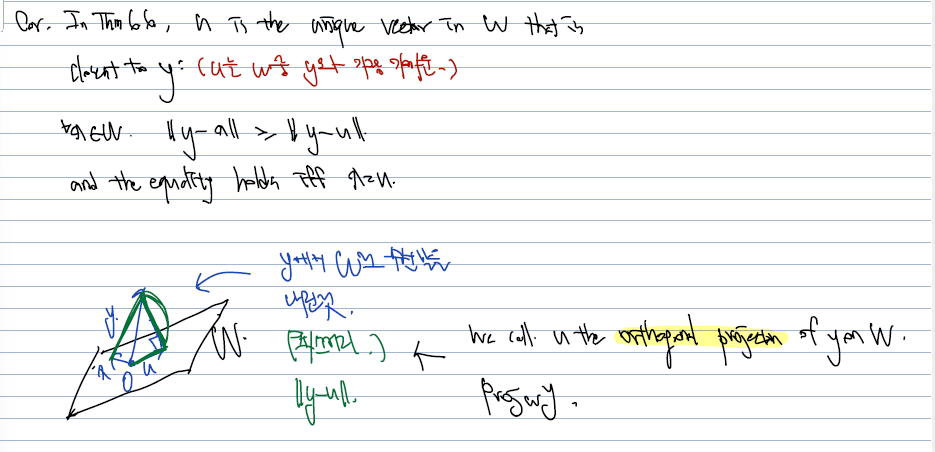
• 즉, y-u 사이의 거리는, u 대신 W위의 다른 임의의 벡터 x를 잡았을 때볻 가장 작게 되고 (수선의 발을 내린 지점이므로 최소거리가 되고), 우리는 이러한 u를 orthogonal projection of y on W 라 한다.

• y를, W에 대해 정사영 (수선의 발을 내린 것) 한 것 이며, 이것이 u가 되는 것이고, 이때의 y와 u의 거리는 다른 y와 W위의 임의의 벡터 x 거리보다 항상 작거나 같다는 것이다.

4. Normed space, Metric space

V가 inner product space 로 주어지면 자연스럽게 따라오는 것으로 V가 normed space 가 된다는 것과 metric space 도 만족한다는 것이 있었다. 위의 normed space 성질 (a,b,c)은 이전 포스팅에서 노름에 대해 다룰 때 이미 학습했던 노름이 주어졌을 때 만족하는 성질들인데, 이걸 가지고 아래의 norms 들이 실제로 normed space 를 이루는지 증명해볼 수 있다.

(1에 대한 증명)

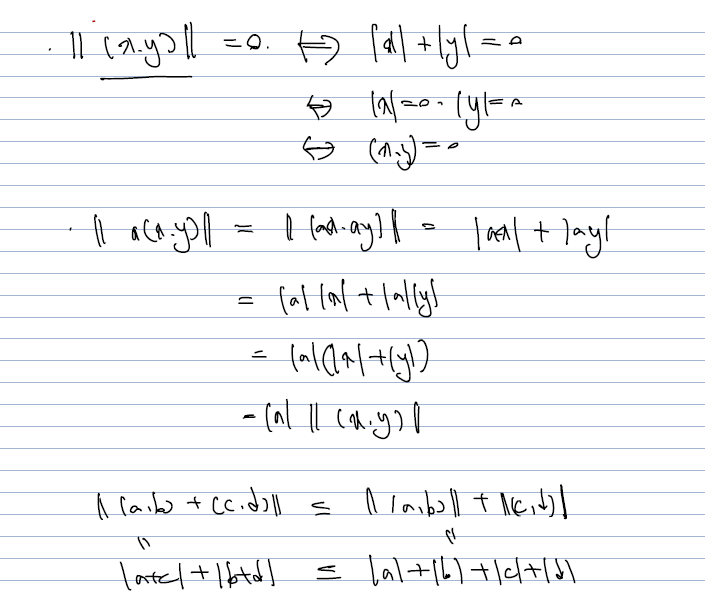
• 정의를 가정으로 사용했을 때 properties 를 만족하는지 확인하면 된다. 그리 어렵지 않음!

(2에 대한 증명)

• (c) 에 대한 증명이 약간 거슬릴 수 있으나.. (|f+g| 의 최댓값이 항상 최댓값|f|+최댓값|g| 보다 작거나 같다는) 그림을 그려서 이해해볼 수 있겠다.

다음으로는 meric space이며, X x X 에 대해 0이상의 실수로 가게 하는 두 벡터의 거리 함수가 된다. 아래 (a,b,c) 를 만족하는 함수가 주어진 공간이 metric space 가 된다.

• 거리를 x 에서 y까지의 거리나, y에서 x까지의 거리를 측정하나 동일하므로 (a)는 자명하고, x에서 y까지 바로 가는 거리가 z를 거쳐가는 거리보다 항상 작거나 같으므로 (b) 도 clear 하다. 거리가 0인 경우는 x = y 인 경우밖에 없다, 로 (a,b,c)를 보다 직관적으로 이해할 수 있다.

여기서 해야할 것은 V가 normed space (노름 연산이 주어진 공간)이라 할 때, d(x,y) = ||x-y|| 로 metric space 를 줄 수 있다는 것인데, normed space properties 를 가지고 위의 definition 이 a,b,c 를 만족하는지 확인하면 된다.

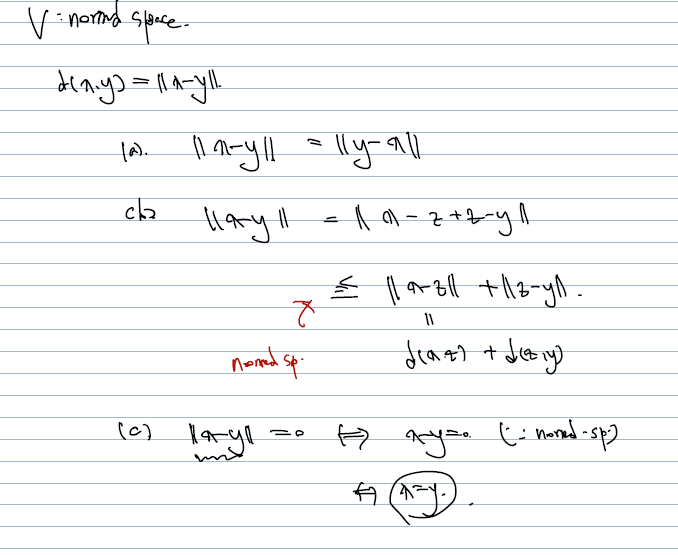
• V 가 normed space 임을 가정했을 때 d(x,y) = ||x-y||가 metric space 를 주게 하는 것 역시 어렵지 않게 보일 수 있다.

여기까지 다룬 것은 V:vector space 가 주어진다면 이 성질들만을 이용해 normed space 를 보일 수 있고, normed space 성질들을 이용해 metric space 를 정의할 수도 있다는 것이다. 그렇다면 이들의 역도 가능할까? 모든 상황에서 그러하진 않다.

1. parallelogram law 가 성립한다면 normed space 에서 inner produce space 를 induce 할 수 있음을 보이기

구체적으로, parallelogram 이 성립한다면, inner product space로부터 normed space V를 induce 하는 것이 가능하다. 이는, normed space 에서 주어진 연산과, parallelogram law 를 추가로 가정했을 때, inner product space (선형으로 쪼갤 수 있고, 순서 바꿀 때 conjugate, 0이 아니라면 양수) 임을 보이는 식으로 증명하면 된다. 아래는 normed space 에서의 다음 연산이 inner product 가 됨을 증명한 것이다.

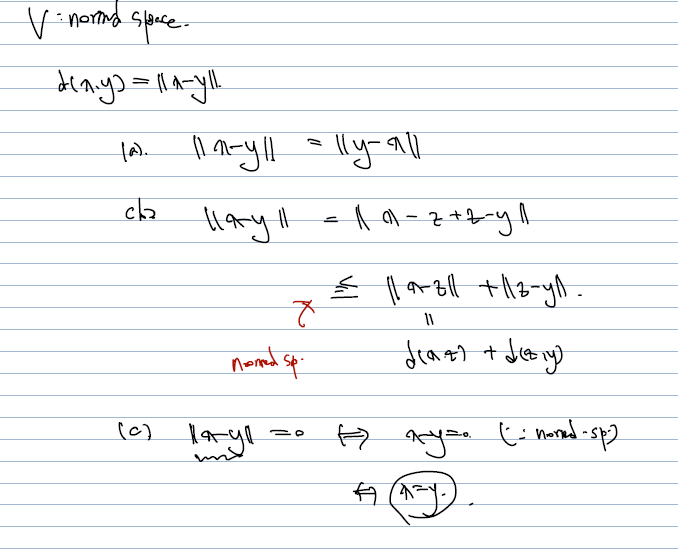
(증명)

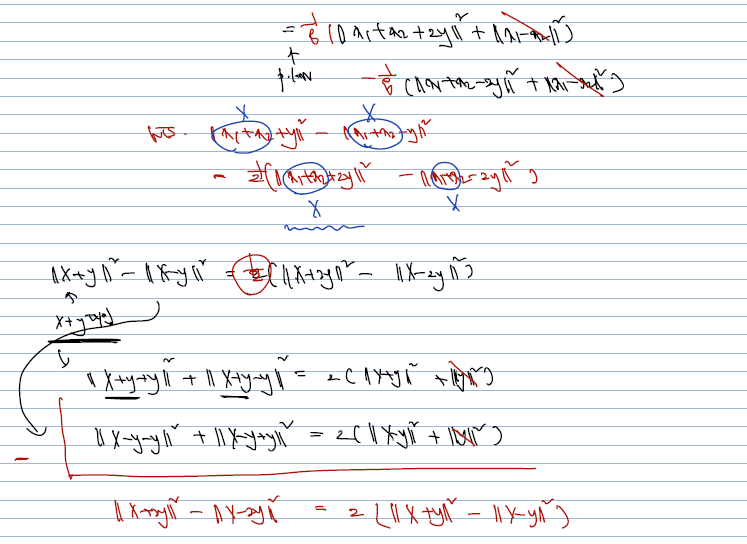
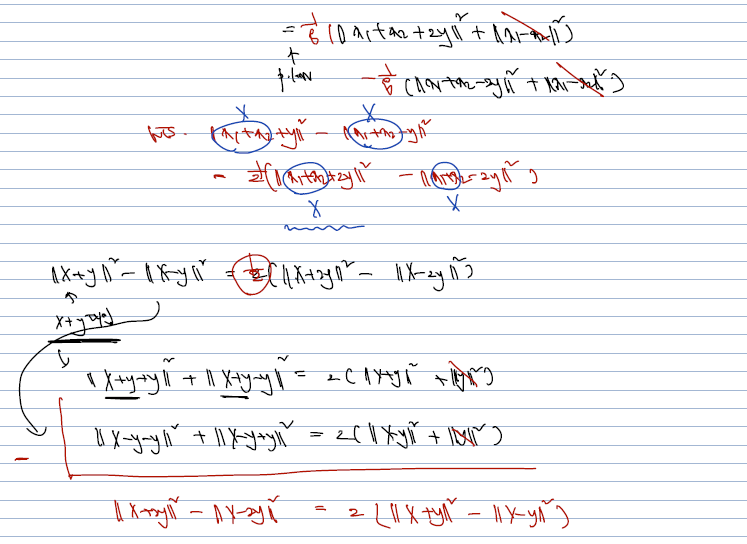
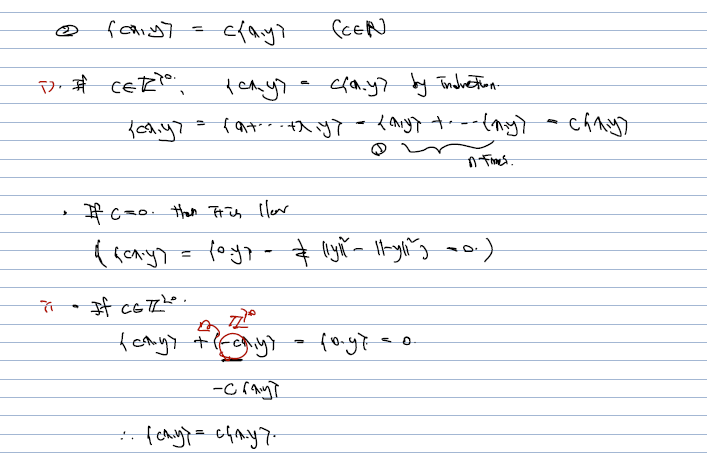
• 각각의 증명이 어렵진 않지만 호흡이 길다. 단순한 계산과 더불어 어느 지점에서 parallelogram law 가 사용되었는지 챙겨두자.

• inner product space 를 가정하지 않고 보여야 하기 때문에, (2) 를 증명할 때도, c가 양의 정수인 경우, 0인 경우, 음의 정수인 경우, 유리수인 경우, 실수인 경우 각각에 대해 나눠서 보여줘야 한다. 물론, 이때의 경우 (1) 덧셈에 대해 쪼개 쓸 수 있다는 것을 보임을 이용하게 된다.

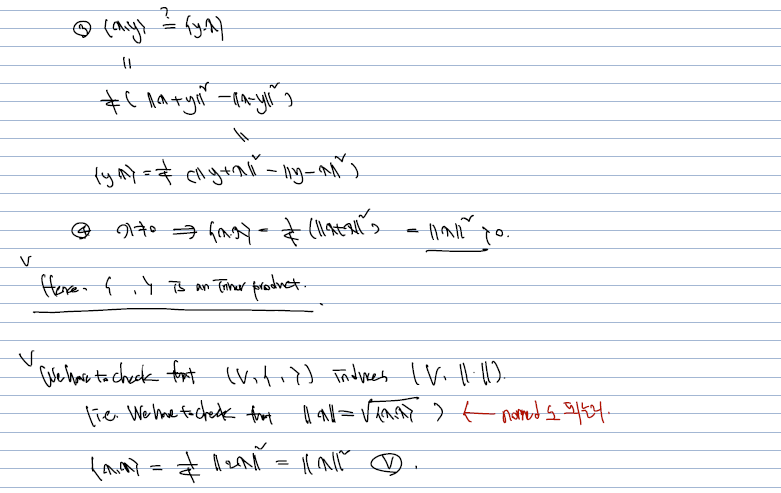
• inner product space (3, 4) 에 대한 증명으로, 정의를 이용하면 어렵지 않게 보일 수 있다.

• 결론적으로 정의된 normed space 는 parellelogram law 가정과 함께라면 inner product 임을 보일 수 있다.

2. metric 이 homogeneous 하고 translation invariant 하다면 metric space 로부터 normed space 를 induce 할 수 있음을 보이기

그렇다면 자연스럽게, metric space 또한 어떠한 조건에서 normed space 로 induce 할 수 있는지에 대한 궁금증이 생길 것이고, 이에 대한 답은 아래와 같다.

-> V: normed space는 metric space d 가 homogeneous 하고, translation invariant 하다면 induce 될 수 있다.

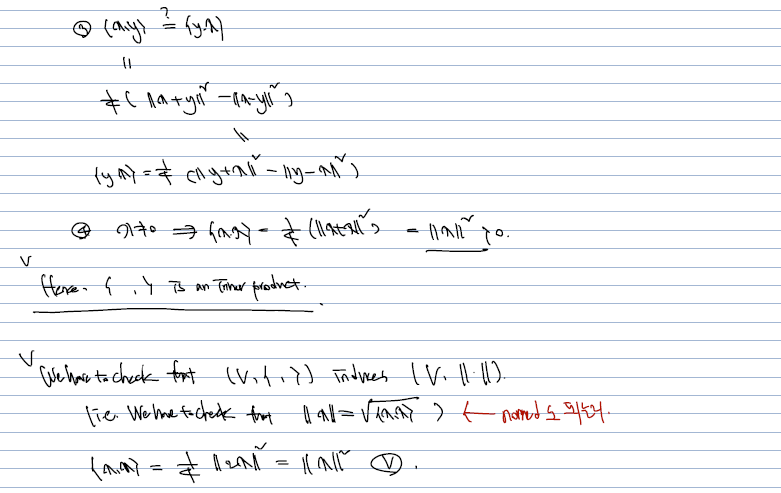
1. metric d 가 homogeneous 하다는 것은, x와 y의 거리에서 각각 둘 다 a배 해준 것의 거리를 구할 때, 기존 x와 y의 거리에 a 상수배 해준 것과 같다는 것이다.

2. metric d가 translation invariant 하다는 것은, x와 y 사이의 거리나, x와 y를 각각 z 에 대해 평행이동한 것 사이의 거리나 같다는 것이다.

두 조건이 주어진 metric space 는 normed space 를 induce 할 수 있다. 아래의 증명을 보자.

(=> 를 증명, V가 normed space 일 때 homogeneous, translation invariant 함을 보이기)

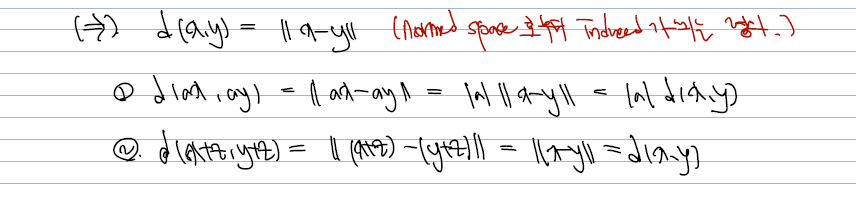
(<= 을 증명, homogeneous 하고 translation invariant 함을 이용해서 normed space 를 유도)

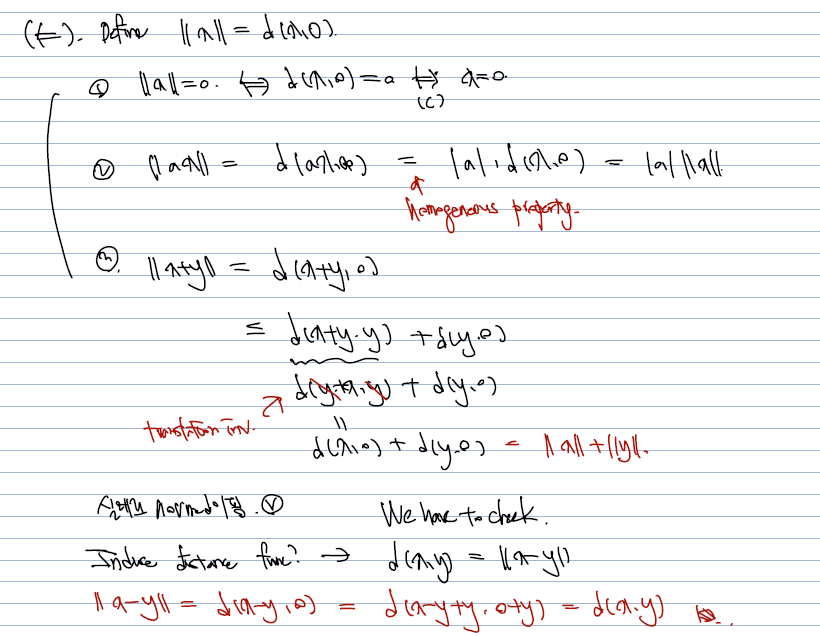
• normed space (2) 번을 유도할 때는 homogeneous property, (3) 번을 유도할 때는 translation invariant 를 쓴다.

정리하자면, inner product V가 주어졌다는 것은 inner produce space 성질로부터 자연스럽게 (다른 조건의 추가 없이) normed space 와 metric space 를 induce 할 수 있다는 것이다. 그러나 역은 그렇지 않고, 특정한 조건이 추가될 경우에만 가능한데, 우리는 normed space 로부터 parallelogram law 를 추가로 가정할 때에 innder product space 를 induce 할 수 있음을 보였다. 또한, metric space 로부터 주어진 metric d가 homogeneous property와 translation invariant 한 정의일 때, normed space 를 induce 할 수 있음을 확인했다.