[Linear algebra] 수반연산자 (The Adjoint of linear operator)

[Linear algebra] 수반연산자 (The Adjoint of linear operator)

기본적으로 adjoint는, 행렬에서 이전에 배웠듯 행렬에 conjugate transpose 를 취하여 얻은 행렬을 뜻한다. 그러나 단순히 adjoint 를 이렇게 정의하는 건 옳지 못하고, 조금 더 깊게 행렬의 adjoint 가 무엇인지, 이걸 가지고 어떻게 활용할 수 있을 지에 대해 알아가보자.

1. T^* = the adjoint of T

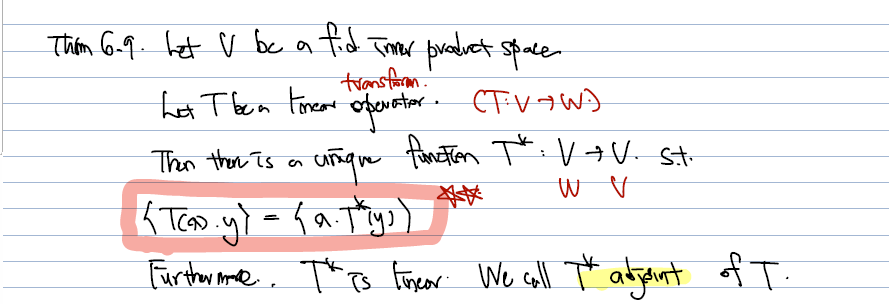
The adjoint of T는, V: finite dimensional inner product space 위에 놓인 linear operator T가 있어서,

• <T(x), y> = <x, T^* (y)> 로 표현할 수 있을 경우에 정의된다.
• 이때 반드시 T가 linear operator: V-> V 가 아니어도 괜찮으며, linear transform 인 경우에 T: V->W 로, T *: W -> V로 정의된다.
• 이를 Adjoint of T 라 부른다.

이에 대한 증명 단계를 보자.

(증명 1: adjoint of T에 맞게 T 정의 후, T* 가 linear 한 지 확인하는 전략)

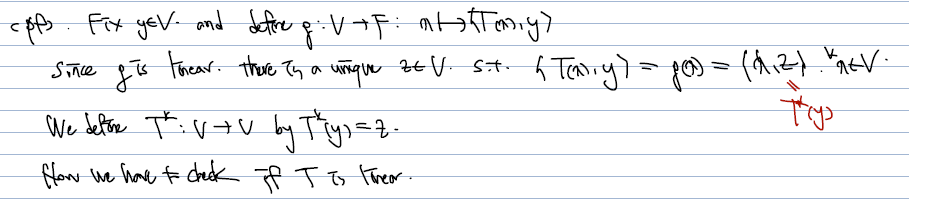
• 증명은, V에서 F로 가는 g(x) 함수를 <T(x), y> 로 정의하고, 이것이 unique 한 z가 있어서 <x,z> 와 같다고 하자. (그럼 여전히 F의 원소가 되므로 g의 정의에 맞는다.)
• 또한 여기서, z = T(z) 라 정의하면 adjoint of T의 정의와 일치하게 되고, 다음은 이렇게 정의를 하더라도 T 가 linear 한 지가 확인이 되면 된다.

(증명 2: T가 adjoint of T의 정의를 사용하더라도 linear 한 지 확인)

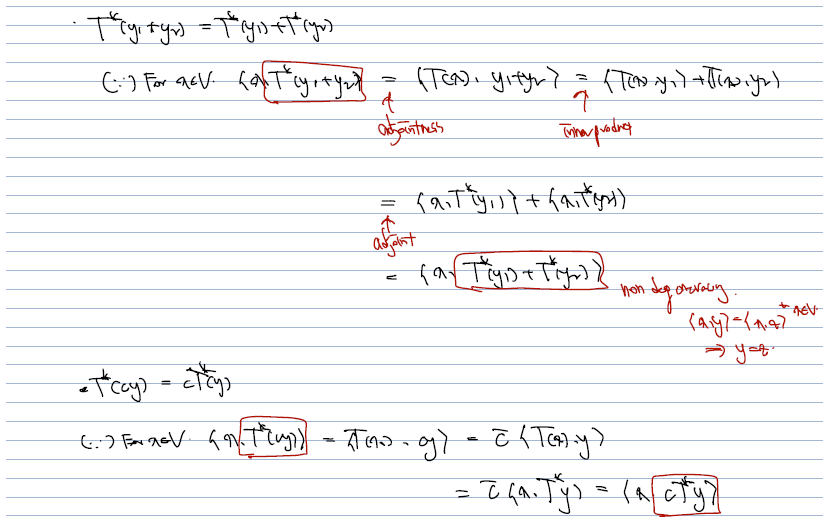
• adjointness (정의), inner product, nondegeneracy (성질) 을 통해 T* 역시 덧셈과 상수배에 대해 쪼개 쓸 수 있어서 linear 함을 확인할 수 있다.

아래의 Remark 까지 챙겨두면 기본적인 adjoint 에 대한 정리가 될 것이다.

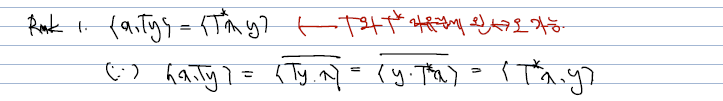
• Theorem 자체는 T* 와 T를 자리 바꿀 때 T가 왼쪽에 있지만, 자리는 상관 없음을 보임.
• V가 finite-dimensional 이 아니더라도, V에서 adjoint of a linear operator 를 정의는 할 수 있다. 그러나 존재성은 모른다.
• linear operator 가 아닌 linear transform 에 대한 adjoint 도 정의할 수 있다.

아래는 linear operator 에 대한 행렬 표현에도 adjoint 를 정의할 수 있음을 보여주며, 이것이 우리가 알고 있던 행렬의 각 성분에 conjugate transpose 를 취하는 연산으로의 adjoint 이다.

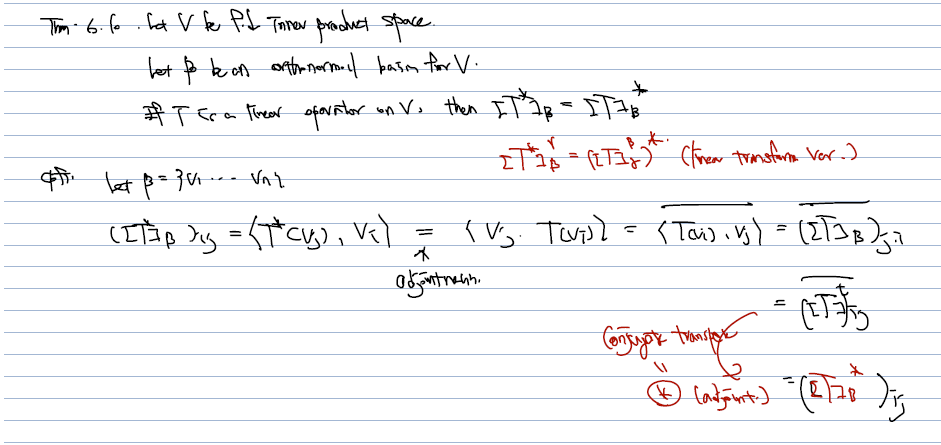
• T 연산을 orthonormal basis 에 대해 i, j 성분으로 표현하면 각각은 <T (v_j), vi> 을 성분으로 가짐을 활용하자. 이는 T linear operator 로 연산을 표현하는데, vi 성분의 각 coefficients 가 T* (v_j) 와 vi 끼리의 내적이었음을 떠올리면 어렵지 않다.
• 후에 자연스럽게 전개하여 conjugate transpose of T를 얻을 수 있게 된다. 따라서 * 는 밖으로 나올 수 있다.

마찬가지로 L_A* 역시 (L_A) 의 adjoint 가 됨을 기억하자.

연습 문제 1.

앞서 배운 정의들을 활용하여 ㄱㄴ단히 문제를 풀어보자. f와 g의 내적으로 정의된 함수에서 orthonormal basis 를 뽑아내고 이를 통해 T*(f) 를 관찰해볼 수 있다.

(1의 해결)

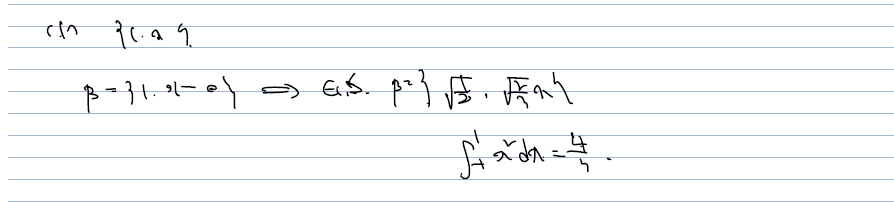
(2 & 3 의 해결)

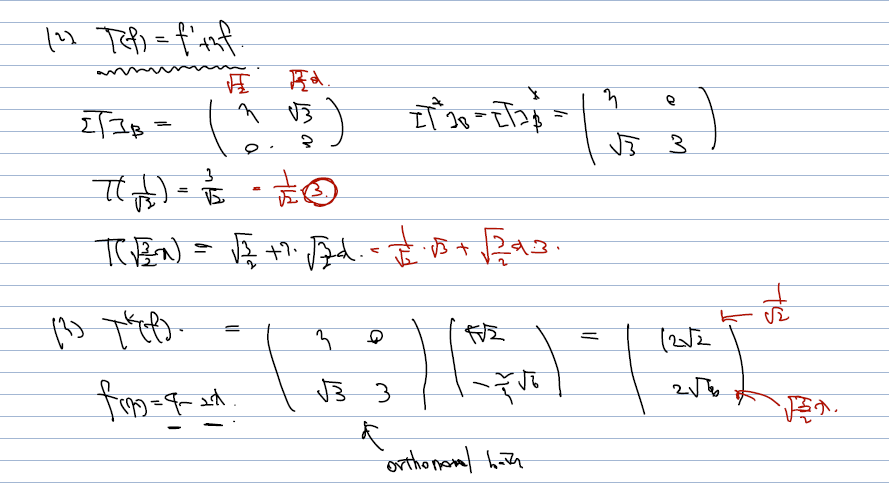
• T를 1에서 발견해낸 orthonormal basis 에 대해 matrix representation 하는 건 어렵지 않고..
• 이걸 T* 의 정의를 활용해 conjugate transpose 해주면 된다.
• f(x) = 4-2x 을 T*(f) 로 쓰라는 문제이다. 따라서, 4-2x 를, adjoint of T에 대해 다시 쓰라는 문제이다.

adjoint에 괄호가 같이 씌여져 있을 때 어떻게 분배하고 자유롭게 다룰 수 있는지, 아래를 보자.

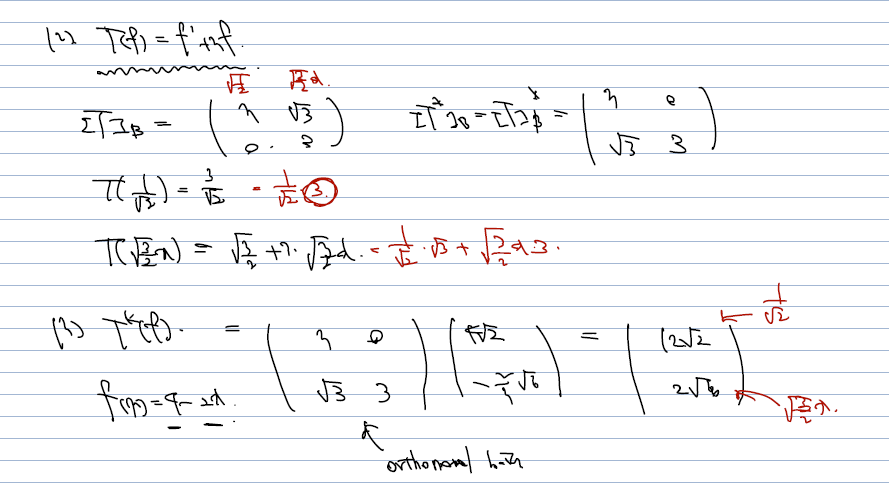
• 행렬에서도 위는 마찬가지로 적용된다. (빨간글씨)
• 이에 대한 proof 는 정의에 맞춰서 쓴다. 즉, <(T+V)(x), y> 가 <x, (adjoint of T + adjoint of V)(y)> 인지 확인하는 식으로 전개한다.
• 증명은 그리 어렵지 않으므로 생략.

이제 adjoint 를 이용해 자유롭게 이를 다루고, 적용할 준비가 되었다. Adjoint 는 몇가지 물리학의 이론이나 통계학, 등의 문제를 푸는데 사용되는데, 아래 applications 을 보며 이에 대한 활용을 확인해보자.

Application 1: Least Squares Approximation

한국말로는 최소제곱근사, 최소승수법 정도로 불리는 Least sqaures approximation 은 이 블로그에서도 여러번 다룬 적이 있으므로 intuition 에서 큰 내용을 할애하진 않을 것이다. 기본적으로, 물리학이나 과학으로부터 얻어낼 수 있는 data sample 이 주어질 때, 이들을 설명할 수 있는 가장 좋은 least square line 을 찾아내는 방법으로,

• 실제 데이터로부터 얻은 y값과
• least square line 으로부터 얻은 expectation y' = ax + b 의 차의 제곱이 가장 적어지는 line 을 찾는 방법이다.

이때 각 y, ax, b 는 어떻게 정의되는지 아래를 보자.

• 목표는 y에서 ax 와 b 값 (모두 least square line 으로부터 얻은 expectation of y값) 을 뺀 것을 최소화하는 것이고,
• 이를 y-Ax 의 norm 으로 조금 간단히 표현한다.
• 이때 y는 데이터로부터의 y 좌표 값, A는 데이터로부터의 x값과 1 값을 각각 하나의 열로, x는 만약 표현하고자 하는 line 이 일차함수라면 ax+b의 형태로 구성되므로 a, b의 열 벡터가 들어간다.
• 따라서 Ax 를 곱하게 되면, 행렬의 곱에 따라 ax1+ b, ax2+b, ..., ax6+ b 의 형태로 표현된다. (데이터 6개라 가정했을 때)

최종적인 질문 (이를 일반화한 질문)은, A matrix M_mxn(F)와 F^m의 원소 y가 있을 때, F^n의 ||y-Ax|| 를 최소화하는 원소 x를 찾는 것이다. (여기서 m은 data sample의 수, n-1은 이를 압축하여 표현하고자 하는 식의 최고차항 차수가 된다. 일차식으로 표현하면 x는 F^2의 원소가 된다.)

본격적으로 해를 구하기 위한 Lemma 를 보자.

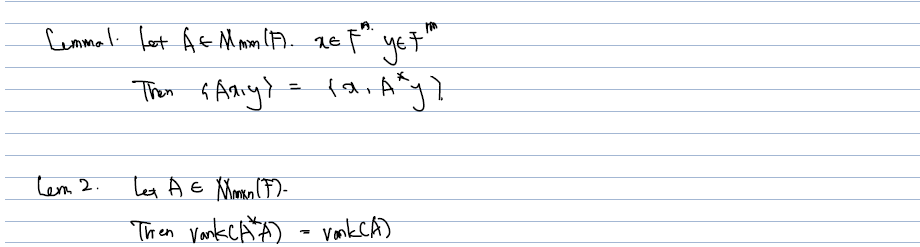
1. A matrix 와 x, y 가 주어졌을 때, 앞에서 다룬 adjoint of 가 그대로 정의되고, 존재한다.
2. rank(A* A) = rank(A) 와 같다.

1은 자명하고, 2에 대한 증명은... dimension theorem (rank-nullity)을 이용해 nullity of A A = numliity of A 와 같음을 보여주면 된다. 따라서 A Ax = 0 <=> Ax = 0 임을 보여주면 되는데, 이는 clear 하다.

이에 대한 보조정리는 다음과 같다.

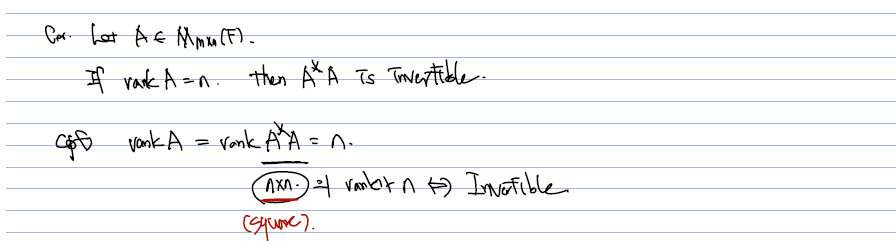
• 만약 A가 full rank 라면, A* A 의 rank 도 full rank 가 되어서, 이것이 통째로 Invertible 하게 된다는 증명이다!

사실은 Lemma 부터 Corollary는 A* A 가 invertible함을 밝혀내기 위함이었고, 이를 이용하면.. ||y-Ax|| 를 최소화하는 해를 구하는 방법을 다음과 같이 쓸 수 있다.

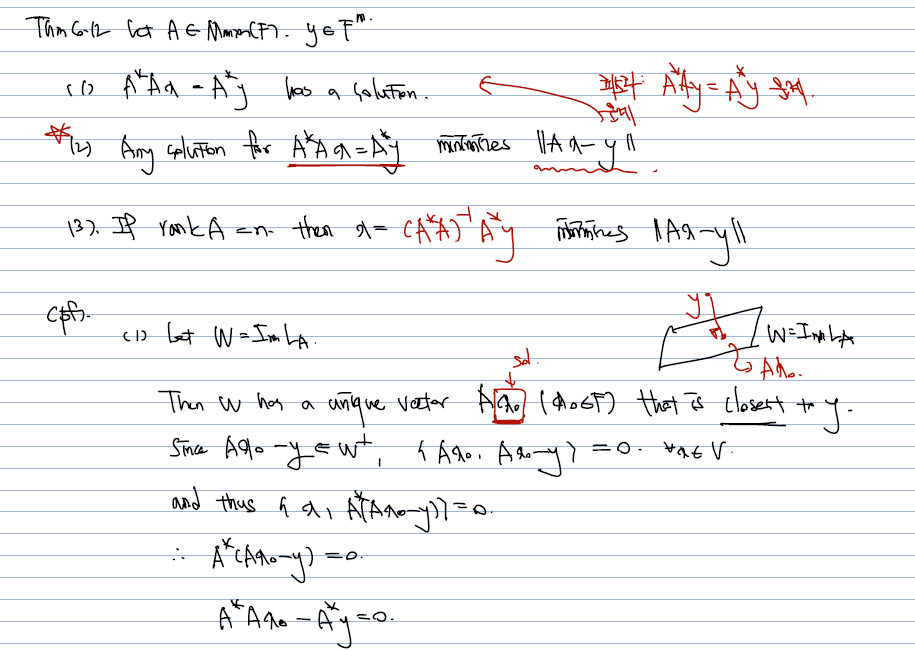
• ||Ax-y|| 를 최소화하는 건, $A^* Ax = A^*y$ 의 해이다.
• 만약 A가 full rank 라면, $x = (A^*A)^-1A^*y$ 로 옮겨서 계산한 것이, ||Ax-y|| 를 최소화하는 해가 된다.
• 증명은, $Ax_o \in W$ 가 W의 원소 중 y와 가장 가까운 벡터가 되고, 따라서 $Ax_o - y$ 가 W perpendicular 공간에 있기 때문에, 이 둘의 내적이 0임을 이용하는 것을 사용한다.

아래의 예시를 직접 보면 이해가 쉽다.

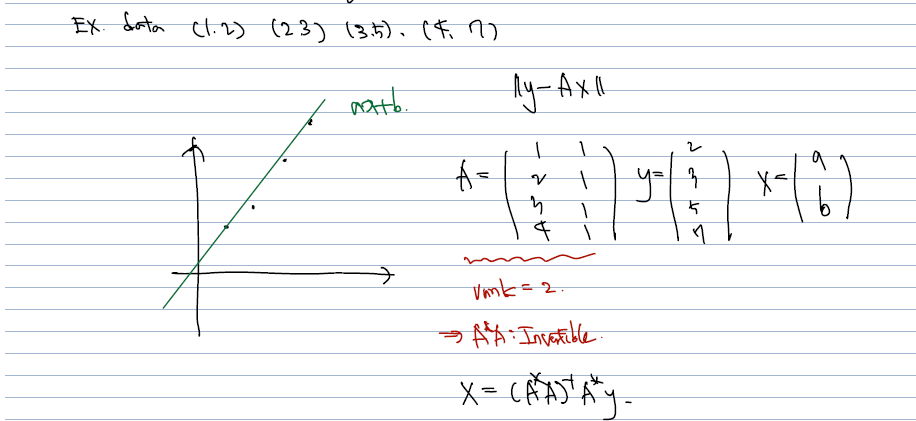
• data (1, 2), (2,3), (3,5), (4,7) 을 모두 지나는 일차식은 없더라도, 이들과 가장 가까운 식을 근사하고자 할 때, A가 full rank (여기서는 =2인지 확인) 한 후 $x = (A^*A)^-1A^*y$ 을 계산하면 된다.

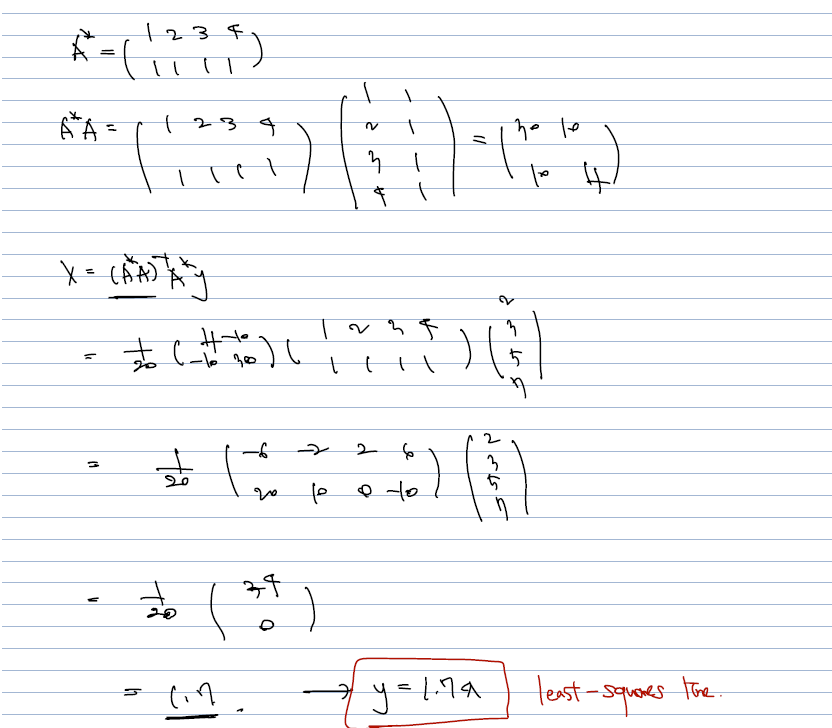
• 나머지 계산은 크게 어려울 것이 없고, 이로부터 얻어낸 결과 (1.7, 0) 를 least square line 의 parameter 계수로 써주면 된다.
• 따라서 y= 1.7x 가 데이터를 가장 잘 표현하는 일차식이 될 것.