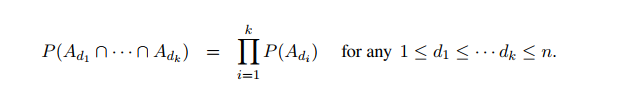[Mathematical Statistics] 1. Probability and Distributions

본 포스팅은 2023-1 성균관대 수학교육과 확률통계학 1의 강의를 바탕으로 이해한 내용을 바탕으로 작성되었습니다. 따라서 수식이나 강의자료의 저작권 역시 이에 있습니다.

1.1 Introduction

• 확률통계의 시작은 random experiment (임의실험)으로 실험의 조건이 same condition 하에 반복되는 것을 전제로 함을 염두에 두자.

• The set of every possible outcome is the sample space (표본공간), 가능한 모든 결과의 집합을 표본공간이라 하고, C로 보통 많이 표시한다.

$\mathcal{C}=\{(x, y): x, y \in\{1,2,3,4,5,6\}\}$.

• 이러한 sample space의 subsets 은 events (사건)이라 한다. 원하는 (궁금한) 사건들을 보통 A,B,C로 표기하곤 한다.

• 만약 주사위의 합이 7이 되는 event B를 표시하고자 한다면

$B=\{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)\}$.

• 확률은? 6/36 = 1/6

1.2 Sets (집합)

(생략)

1.3 The probability set functions (확률집합함수)

• collection of events 인 Borel sets 의, 각 elements 에 대해 확률을 assigns 해주는 것이 필요하다. (define set functions)

• 그러나 이를 이해하기 위해 선행적으로 sigma-field 가 무엇인지에 대한 이해가 필요하다.

Definition (sigma-field).: C 집합들의 집합!

(i) $\phi \in \mathcal{B}$.
(ii) $C \in \mathcal{B} \Rightarrow C^c \in \mathcal{B}$ (closed under complement).
(iii) $C_1, C_2, \cdots \in \mathcal{B} \Rightarrow \bigcup_{i=1}^{\infty} C_i \in \mathcal{B}$ (closed under countable union).

종합하면, (i) 공집합도 포함해야 하는 것이며 (ii) subsets C나 그의 complement 도 포함하고, (iii) 나아가 countable union 에 대해 closed 된 필드를 의미한다.

단, 마지막 countable union 에 의해 countable intersection 에 대해 closed 임을 증명할 수도 있다. (드모르간 법칙!)

시그마-필드의 예시는 다음과 같다. (서로 다른 시그마 필드임)

1. $\mathcal{B}=\left\{\phi, C, C^c, \mathcal{C}\right\}$.
2. $\mathcal{B}$ is the power set of $\mathcal{C}$, i.e. the collection of all subsets of $\mathcal{C}$.
3. $\mathcal{B}=\bigcap_{i=1}^{\infty}\left\{\varepsilon_i: \mathscr{D} \subset \varepsilon_i, \varepsilon_i\right.$ is a $\sigma$-field $\}$. This is the smallest $\sigma$-field which containing $\mathscr{D}$, and it is called the $\sigma$-field generated by $\mathscr{D}$.
4. Let $\mathcal{I}$ be the set of all open intevals in $\mathbb{R}$ (set of real numbers), then the $\sigma$-field generated by $\mathcal{I}$ is called the Borel $\sigma$-field.

4번의 경우, I가 R 내에서 열린 구간 집합이라 할 때, 그러면 I에 의해 만들어진 시그마 필드는 Borel $\sigma$-field 임을 말한다. 예컨대 (a,b) 와 같은 원소들도 포함하며, 계구간, 폐구간을 원소로 포함이 가능함을 말한다.

Definition (Probability): C를 sample space 라 하고, $\mathcal{B}$ 를 시그마-필드라 하자. P는 $\mathcal{B}$에서 정의된 real-valued function 이라 하자. 그러면 P는 다음 세가지 조건을 만족시킬 때 probability set function (probability measure) 이라 정의됨.

(1) $P(C) \geq 0$ for all $C \in \mathcal{B}$
(2) $P(\mathcal{C})=1$
(3) If $\left\{C_n\right\}$ is a sequence of events in $\mathcal{B}$ and $C_m \cap C_n=\phi$ for all $m \neq n$, then

(1)을 non-negativity 조건이라하며, (3)을 countable additivity 라 한다. (3)에 대한 증명을 잠깐 하자.

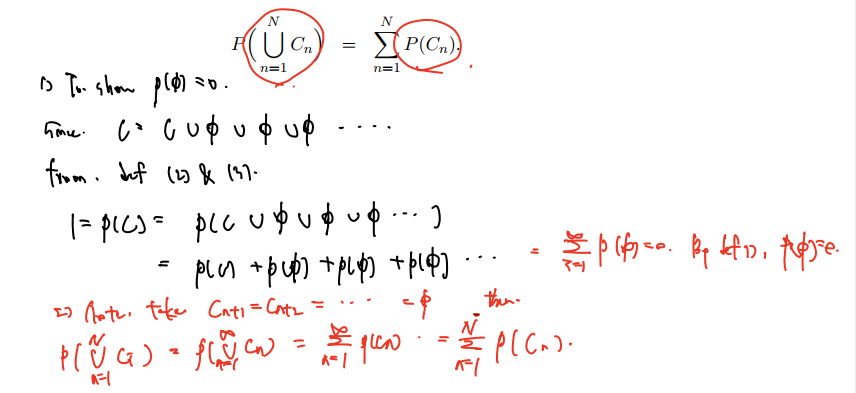
• 집합 Cn을 넘어서는 n+1, n+2 ... 에 관련해선 공집합이라 두고
• 따라서 union 들을 N까지부터 무한대까지로 확장할 수 있다.
• 그런데 이 값은 정의에 의해 1이다. 따라서 시그마를 포함한 합으로 변경하고,
• 다시 N까지의 합으로 돌아오면 된다.

이제 다른 terms 들을 살펴보자.

Terms

• A collection of events whose members are pairwise disjoint, that is $C_m \cap$ $C_n=\phi$ -> 상호배반이라 한다.
• The collection is further said to be exhaustive if the union of its events is the sample space, that is $P\left(\bigcup_{n=1}^{\infty} C_n\right)=1$.

• A mutually exclusive and exhaustive collection of events forms partition a of $\mathcal{C}$.

첫번째와 두번째로부터 partition 이란 개념이 나오고, 그림은 다음과 같다.

증명 For each event $C \in \mathcal{B}$, we have $P(C)=1-P\left(C^c\right)$.

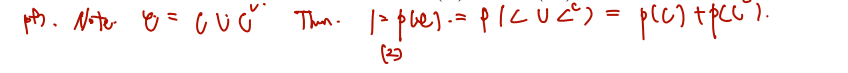
증명 If $C_1$ and $C_2$ are events such that $C_1 \subset C_2$, then $P\left(C_1\right) \leq P\left(C_2\right)$.

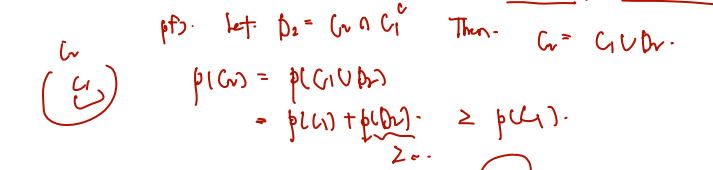
증명 If $C_1$ and $C_2$ are events in $\mathcal{C}$, then

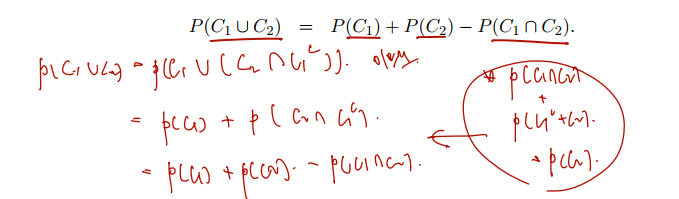
Continuity of Probability Functions

Let {Cn} be a nondecreasing sequence of events. Then,

$\lim _{n \rightarrow \infty} P\left(C_n\right)=P\left(\lim _{n \rightarrow \infty} C_n\right)=P\left(\bigcup_{n=1}^{\infty} C_n\right).$

C2가 C1를 포함하고, C3이 C2를 포함하고, ... 반복되는 nondecreasing events 일 때, 이들의 집합의 극한의 확률을 구한다는 것은 각 집합의 union 의 결과와 같다는 것.

Let $\left\{C_n\right\}$ be a nonincreasing sequence of events. Then,

반대로 nonincreasing 계속 작아지는 사건이라면 Intersection 의 결과가 각 확률의 극한과 같다는 것.

Boole's Inequality Let $\left\{C_n\right\}$ be an arbitrary sequence of events.

Then,

이는 countable sub additivity ㄹ 부르기도 한다.

1.4 Conditional probability and independence

Definition: B와 A를 P(A)>0 일 경우의 각각 사건이라 한다면, A가 주어졌을 경우 B의 조건부 확률은 다음과 같다.

(Properties) Let $A, B, B_1, B_2, \ldots$ be events with $P(A)>0$. Then,
1. $P(B \mid A) \geq 0$
2. $P(A \mid A)=1$
3. $P\left(\biguplus_{n=1}^{\infty} B_n \mid A\right)=\sum_{n=1}^{\infty} P\left(B_n \mid A\right)$, provided that $B_1, B_2, \ldots$ are mutually exclusive.

앞서 확인한 조건 3가지를 모두 조건부 확률에서도 확인할 수 있다.

Theorem: The law of total probability (전 확률의 정리, 전 사건의 정리)

전사건의 정리는 익숙한 개념인데, A1, ..., Ak를 C의 partition 이라 하고 P(A) >0, 서로 다른 사건에 대해 P(B) > 0 이라 할 때,

$P(B)=\sum_{i=1}^k P\left(A_i\right) P\left(B \mid A_i\right)$.

이에 대한 증명은 다음과 같다.

(전 사건의 정리 증명, 조건부확률 사용)

Theorem: Bayes' Theorem
역시나 익숙한 베이즈 정리는, 전 사건에서 궁금한 사건 Aj 의 조건부 확률을 분자로 한 것이다.

$P\left(A_j \mid B\right)=\frac{P\left(A_j\right) P\left(B \mid A_j\right)}{\sum_{i=1}^k P\left(A_i\right) P\left(B \mid A_i\right)}$

Independence
-> let A and B be two events. 이때 A와 B가 독립이라면 두 사건의 각 확률의 곱 = 두 사건 intersection 의 확률과 같다.

만약 사건 A1, A2, A3 가 mutually independent (서로 독립) 이라면?

더 general 하게 서술하자면 events A1, ...An이 mutually independent 일 때, 이들의 collection of k개는 (2 <= k <= n) 다음과 같이 연속된 곱으로 표현이 가능하다.