[Mathematical Statistics] 1. disc r.v., conti r.v., pmf, pdf, cdf, Transformations

(약간의 정리, Recall)

sigma-field 는 임의의 조각모임을 모두 원소로 하는 집합 모임이라고 했다. 여기서 나아가 borel set 은 열린집합들을 포함하는 가장 작은 sigma-field 를 borel set 이라 하고, C, C의 complement, countable union, countable intersection 을 원소로 포함한다고 하였다.

이런 집합모임 field 를 F라 할 때 F에서 continuous value 한 집합으로 매핑을 해주는 것이, 확률 p (0,1] 이며 이로부터 3가지 성질을 유도할 수 있었다.

1.5 Random variable (확률변수)

확률변수의 정의는 다음과 같으나

"A function X: C -> R is called as a random variable"

전체 집합에서 r.v num 으로 매핑하는 X를 확률변수라고 간단하게 정의하고 넘어갈 수 있으나, 조금 더 엄밀한 정의를 알아보도록 하자.

Definition random variable (more rigorous definition). $A$ function $X: \mathcal{C} \rightarrow \mathbb{R}$ from a sample space $\mathcal{C}$ equipped with a $\sigma$-field $\mathcal{F}$ to $\mathbb{R}$ is called as a random variable if for any $a \in \mathbb{R}$, the preimage $X^{-1}((-\infty, a)) \in \mathcal{F}$.

Definition random variable (equivalent definition of 1.5.1a). A function $X: \mathcal{C} \rightarrow \mathbb{R}$ from a sample space $\mathcal{C}$ equipped with a $\sigma$-field $\mathcal{F}$ to $\mathbb{R}$ is called as a random variable if for any Borel set (an element of th Borel $\sigma$-field) $B \subseteq \mathbb{R}$, the preimage $X^{-1}(B) \in \mathcal{F}$.

아래가 위보다 보다 엄밀한 정의에 속하나, 결국 동치이다. 아래를 먼저 살펴보자. 기존과 비슷하나 추가된 점들이 있다.

• 전체집합 C는 시그마 필드 F를 전제로 한다는 점
• 실수 전체 집합 R의 부분집합으로 Borel sigma-field 가 있어서, 이의 역상(preimage)가 또다시 시그마 필드 F의 원소가 된다는 점.

이 추가된다. 이를 위의 정의와 연결 지으면, random variable 이 C를 R로 매핑해주는 function 이라 할 때, R의 원소 임의의 실수 a에 대해 -무한대부터 a까지 범위의 역상은 모두 F의 원소가 된다는 것이다.

이를 좀 더 직관적으로 바라봐보자. 흔히 우리가 이야기하는 P(X=3)이라는 확률은 X=3이라는 확률변수에 대한 확률을 의미한다. 그러나 엄밀히 표기하면 이 표현은 p({C: X(C) = 3}) X(C) = 3이 되는 C들의 모임을 의미하며, 이것이 sigma field F의 원소가 되어야 한다는 것이다. 따라서 보다 엄밀한 정의는 단순히 C에서 R로 매핑하는 연결을 정의로 끝내는 것이 아니라, 각 field 의 정의까지 포함해서 원소 집합의 개념까지 연결하는 것이다.

여기서도 실제 문제를 상상할 수 있다. 서로 다른 동전 2개를 던져 Tail이 나온 횟수를 확률변수로 정의할 때, B에 들어갈 수 있는 집합은 {0}, {1}, {2} 이며, 각각 매핑되는 c는 또다시 0일 때 (H,H), 1일 때 (H, T) (T, H), 2 일 때 (T, T) 이며 이에 따라 확률이 정해진다고 보면 된다.

Px는 induced probability by r.v. X 라 부른다.

• P(C)는 sigma-field F 위에서 정의되고, Px(B)는 borel sigma-field 위에서 정의된다.
• 아래는 모두 같은 확률이다.

그럼 이제 (실제로는) 더 넓은 sigma field F의 원소인 C 위에서 정의된 확률을 마치 $\mathcal{B}(\mathbb{R}))$ 에서 정의된 확률인 것 처럼 쓸 수 있다.

Probability mass function (pmf)
이에 대한 예시가 X가 disc r.v. 일 때 확률인 pmf 이다.

• px() 는 [0,1] 의 값을 가진다.

Def) Cumulative Distribution Function
pmf 를 알았다면 이제 이에대한 '누적분포함수 / 분포함수'인 cdf 를 정의할 수 있다. random variable X에 대해 cdf 는

따라서 cdf 는 확률변수 X가 small x 안에 들어있을 확률을 누적하여 그린 것이며, X(c)의 관점에서 (-무한대, x] 구간의 원소가 X(c)인 c 이기도 하다.

cdf 는 확률분포 X가 discrete 한지 continuous 한지에 따라 다르게 그려진다. discrete X에 대한 cdf의 그래프는 어떨지 상상해보자. 어쨌든 구간 내에서 누적하여 그리는 것이므로 연속인 구간이 있을 것인데, 반대로 P(X=3) 과 같은 구간에서 0 이상의 값을 가질 것이므로 불연속 jump 되는 지점도 있을 것이다. 다음을 비교하면 이해가 쉽다.

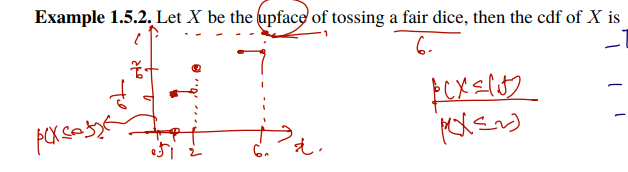
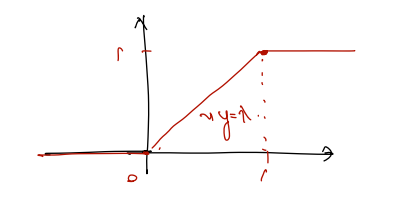
위는 X가 disc 할 경우이고, 아래는 X가 continuous value 일 경우이다. 예컨대 X가 구간 (a,b)에 속할 확률은 그 구간의 길이에 비례한다. 만약 구간이 (0, 1)이라면 0과 1 사이에서 cdf 는 y = x 증가함수를 따를 것이다.

cdf 에 대한 4가지 성질을 보고 이를 증명하자.

1. for any $a<b$, then $F(a) \leq F(b)$ ( $F$ is nondecreasing)
2. $\lim _{x \rightarrow-\infty} F(x)=0$ (the lower limit of $F$ is 0 )
3. $\lim _{x \rightarrow \infty} F(x)=1$ (the upper limit of $F$ is 1 )
4. $\lim _{x \downarrow x_{0}} F(x)=F\left(x_{0}\right)(F$ is right continuous $)$

(1) 의 pf.

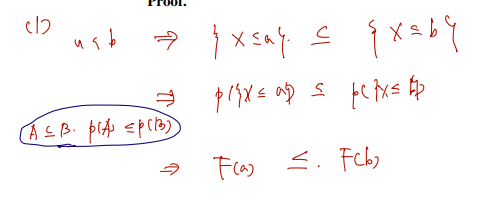
(2)의 pf.

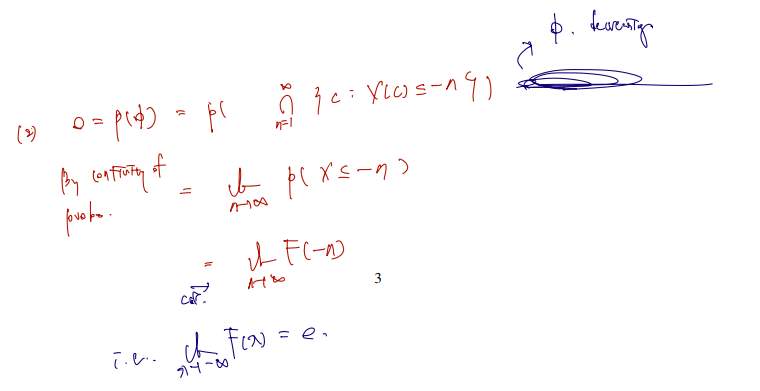
(3)의 pf.

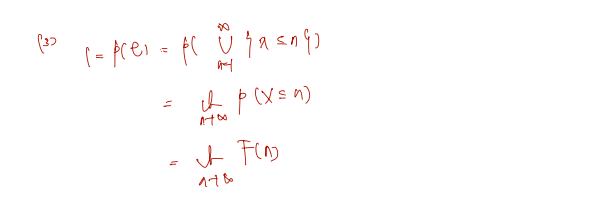
(4)의 pf.

다음은 이어지는 cdf 를 활용한 몇가지 증명들이다.

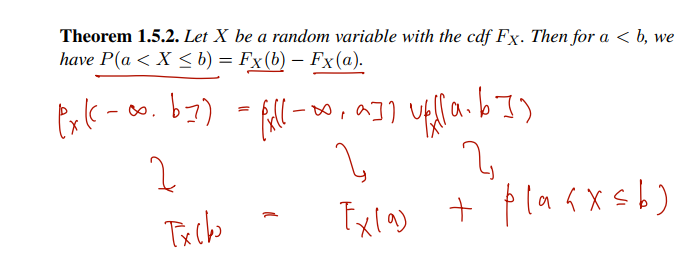
(P(X= x) = Fx의 불연속적 jump 의 크기 = Fx의 x에서 함숫값과 좌극한의 차임을 증명)

1.6 Discrete random variables (이산형 확률변수)

Definition (Discrete random variable, Durrett 2019). A random variable $X$ and associated probability measure $P$ is said be discrete (이산형의) if there exists a countable set $S \subseteq \mathbb{R}$ such that $P_{X}\left(S^{c}\right) \equiv P\left(X \in S^{c}\right)=0$.

countable sets S가 존재하며 이 S 의 complement 가 등장할 확률은 0 이 존재할 때 이산형 확률변수 X 라 정의한다.

이산형 확률변수의 pmf 정의는 다음과 같이 쓸 수 있으며 수학적으로 다루기 편하게 하기 위해 px 정의역을 countable set S가 아닌 전체실수 R로 확장하여 쓰기도 한다. 그러나 이 역시 S에 속하지 않은 R에 의 원소에 대해서는 P(x) = 0 으로 정의한다.

Definition (Probability mass function, pmf). Let $X$ be a discrete random variable that has countable set $S \subseteq \mathbb{R}$ such that $P\left(X \in S^{c}\right)=0$. The probability mass function (pmf, 확률질량함수) of $X$ is defined by

• The support S는 pX(x) > 0 이 되는 X의 포인트들의 집합을 뜻한다.

• pmf 의 필요충분조건: countable set S가 존재하고, p(): S -> R를 만족할 때 다음을 만족한다.

1.7 Continuous random variables (연속형 확률변수)

연속형 확률변수는 random variable X가 continous 한 값일 경우를 뜻하고, 이는 'cdf Fx 가 임의의 실수 x에 대해 continous function' 일 경우에 가능하다. (cdf의 좌극한 = 우극한 = 함숫값인 경우)

이 경우에 P(X=x) 값이 0인 이유는 연속형 확률변수를 다루는 이상 한 점에서의 확률은 관심 밖이기 때문이다. (0이기 때문이다.) 구간에서의 확률의 차로 이가 0임을 쉽게 확인할 수 있다.

구간에서의 확률을 정의해야 하는 연속형 확률변수의 경우, 확률질량함수 (pmf)를 쓰지 않고 확률밀도함수 (pdf)를 쓴다. pdf 의 정의는 다음과 같다.

Definition (probability density function). Let $X$ be a continuous r.v. with $c d f F_{X}$. If there exists a nonnegative function $f_{X}: \mathbb{R} \rightarrow \mathbb{R}$ such that

즉, 확률밀도함수 pdf 는 이미 정의한 누적분포함수 cdf 의 form 에서 이해하는 것이 좋으며, pdf를 정의하기 위해 pdf의 (-무한대, x) 까지의 integral이 cdf 라는 의존적인 정의를 쓴다.

• 만약 cdf 가 미분 가능하다면, cdf' = pdf 라고 편하게 쓸 수 있다.

• cdf 의 미분 가능성은 직접 해봐야 아는 것이다. 예컨대 cdf 는 연속임을 가정하기 쉽지만 이산형확률변수의 cdf 도 존재하며 불연속을 포함하여 그릴 수 있기 때문이다.

• pdf 는 다음의 성질을 지닌다.

  $\begin{aligned} & -f_{X}(x) \geq 0 \text { for all } x \in \mathbb{R} \\ & -\int_{-\infty}^{\infty} f_{X}(t) d t=1 \end{aligned}$

• cdf 의 미분인 pdf 는 함숫값 자체의 의미를 생각하지 않는 것이 좋다.

• f(x) > 0 인 x들의 모임을 support of X라 하며 다음과 같다. $\operatorname{supp}(X):=\left\{x \in \mathbb{R}: f_{X}(x)>0\right\}$.

• pdf 의 함숫값 자체의 의미는 없으나 구간이 정의되었을 때 (어떤 a < b 임의의 구간만 있으면), 구간 내 확률을 pdf 의 적분으로 편하게 생각할 수 있다는 점.

  $\begin{aligned} P(a<X \leq b) & =P(a \leq X \leq b) \\ & =P(a \leq X<b) \\ & =P(a<X<b) \\ & =\int_{a}^{b} f_{X}(t) d t . \end{aligned}$

다음의 주어지는 예시를 꼼꼼히 따져보자.

(Example)

• Suppose a point is selected at random in the interior of a circle of radius 1. Let $X$ be the distance of the selected point from the origin.

X를 radius 1 circle 내에서 점을 찍었을 때 원점 사이의 거리라 할 때, 이에 대한 cdf 를 정의하는 문제이다. (cdf를 정의하고 미분 가능함이 확인되면 pdf 를 구할 수도 있다!)

• For $0<x<1$, the event $\{X \leq x\}$ corresponds to the point lying in a circle of radius $x$ centered at the origin. Thus,

사건 $\{X \leq x\}$은, sample space는 radius 1로 고정인 원 안에서 radius x 가 변할 때 X < x 에 대응하는 경우를 말한다. 따라서 3가지 case 로 나눠 누적분포함수를 정의할 수 있다. 중요한 건 x가 0과 1 사이일 경우이며, 이 경우 radius x인 원의 넓이/radius 1인 전체 원의 넓이로 정의할 수 있다.

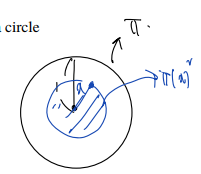
그래프를 그리면 연속인 미분가능함수이고, 이를 미분하면 pdf 도 확정 가능하다.

잠깐 확률변수의 Transformations 에 대해 생각해보자.

Transformations Example 1

pdf of $Y=X^{2}$ 를 찾아야 하는 문제라면 어떨까? 다음과 같은 순서를 거치면 편하다.
1. support of Y를 찾는다. 이 경우 Y는 X를 거쳐왔으므로 support of X에서 출발한다.
2. Sy를 찾았다면, 이 위에서 $P(Y \leq y)$ 인 cdf 를 찾는다.
3. 변수변환을 적용한 구간에서의 cdf 를 찾는다.
4. 미분하여 pdf 를 구한다.

결국 변환의 pdf를 구한다는 것은 -> 변환의 cdf 를 구한다음 -> 미분하여 변환의 pdf 를 구하는 과정을 거친다는 것인데, 바로 pdf 끼리의 변환은 안되는지에 대한 논의는 후에 서술한다. 일단 해당 example 의 풀이.

Transformations Example 2
Find the pdf of $Y=X^{2}$ when $f_{X}(x)=\frac{1}{2} I(-1<x<1)$.

Transformation: pdf 끼리의 변환
곧바로 pdf 끼리의 변수 변환은 안될까? 이 경우 transformation이 one-to-one / differentialble 이어야 하는 전제가 붙는다. 이유는, 예컨대 $Y = g(X)$ 의 변수 변환을 하여 Y의 pdf 를 곧바로 정의할 때 $g(X)$ 의 역함수와 미분이 포함되기 때문이다. 정확한 식은 다음과 같다.

• Let $X$ be a conti, r.v with pdf f(x) and support Sx
• Let Y = g(X)
• g(x) is a 1-1 and differentiable function on the supprot of X, Sx,

then the pdf of Y is given by

Transformation: pdf 끼리의 변환 증명
증명은 어렵지 않게 확인할 수 있다. g가 increasing 또는 decreasing 이므로, 2가지 case 에 대해 증명을 보이고 general form 은 절댓값을 쓴다.

First, assume $g$ is increasing.

Next, if $g$ is decreasing, then

Transformation: pdf 끼리의 변환 Example 1
Find pdf of $Y=-2 \log X$, where $f_{X}(x)=I(0<x<1)$.

정의에 따르면 어렵지 않다.

(sol) From $g^{-1}(y)=e^{-y / 2}, d x / d y=-\frac{1}{2} e^{-y / 2}$,