[Mathematics] Taylor's series (Taylor's expansion), Maclaurin's series

테일러 급수(Taylor's series)

복잡한 함수 y = f(x) 에 대해서 우리가 잘 모르는 함수를 다항함수로 바꿔서 사용하는 것을 테일러 급수, Taylor series 라고 한다. (Taylor expansion 도 같은 의미로 사용되곤 한다.)

함수를 다항함수로 바꾸는 이유는 무엇일까?

• 수학적으로 와닿게 정의하기 위함
• 미분 가능하다는 조건을 이용하여 분석 가능
• 앞의 계수 분석

등이 있을 거 같다. 이 부분은 뇌피셜..

그렇다면 복잡한 함수를 다항함수로 바꾸는 테일러 급수에 대해 자세히 알아보자.

조건

테일러 급수가 성립하기 위해서, 한 가지 조건이 필요한데 그것은 y = f(x) 함수가 x = a 에서 무한번 미분가능해야 한다는 것이다.

왜? x = a 에서 무한번 미분가능해야 성립하도록 식을 짜놓았기 때문에😅이다.

동어반복이라고 느낄 수도 있겠지만, 테일러 급수에 대해서 온전히 설명을 마치고 나면 이해가 될 것이다.

테일러 급수

그렇다면 본격적으로 테일러 급수 식을 보자.

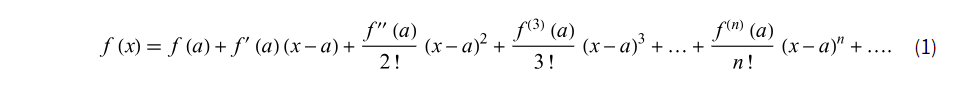
이를 정리하면 복잡한 함수 f(x) 는 다음과 같은 덧셈으로 이루어진 다항식으로 정리할 수 있다.

• $f^n$ 는 f를 n번 미분한 것이다
• n! 는 n의 팩토리얼이다.
• 풀어서 설명하면, f(x) 가 x = a 에서 무한번 미분가능할 때 f(x)가 다항식이 아니라면, f(x) 에 a 를 대입한 것과, f(x) 를 한 번 미분한 것에 a를 대입하고, x-a 를 곱한 것과 ... 식들의 합으로 표현할 수 있다.

증명

어떻게 다음과 같은 식으로 다항함수가 아닌 식이 다항함수로 표현될까?

증명을 위해서 f(x) 함수를 x = a 에서 무한번 미분가능하다고 하고, 다항함수로 나타낼 수 있다고 할 때의 상황을 가정해보자. 그리고 각 항의 앞의 계수를 c0, c1, c2, c3 .. 으로 표현하자.

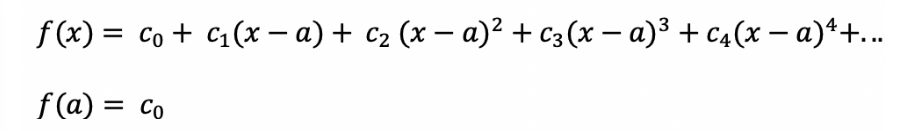
첫번째 미분하지 않고 a 를 넣었을 땐 c0 이 등장한다.

위의 식을 a에 대해 한 번 미분하고, a 를 대입하면 c1 이 등장하게 된다.

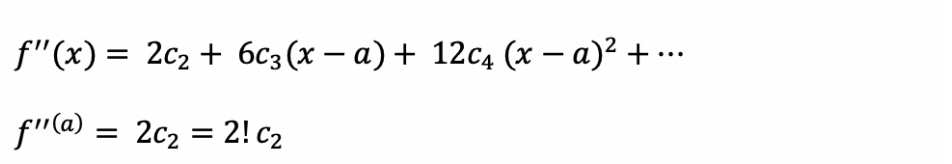
위의 식을 또다시 a에 대해 미분 (원래 식을 2번 미분)한 식에 a 를 대입하면 2c2가 나오게 된다.

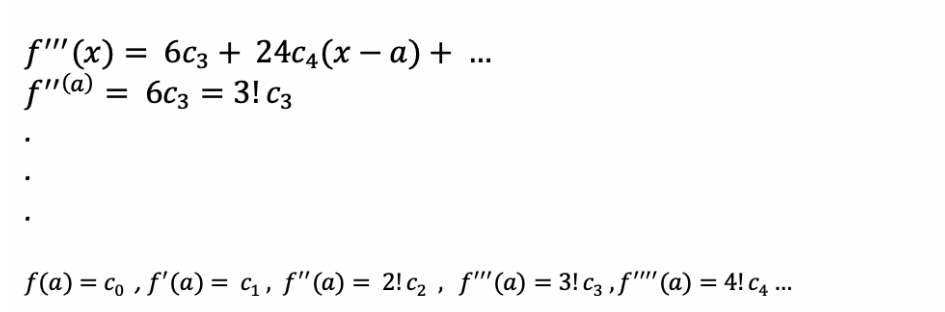
3번 미분, 4번 미분을 반복해서 얻은 식에 따르면 $f^n(a) = n! X c_n$ 으로 표현할 수 있다.

따라서 이를 c에 관한 (즉 다항식 계수에 관한 식으로 정리하게 되면) 다음과 같다.

$c_n = f^n(a) / n!$

이 값을 앞서 x = a 에서 무한번 미분가능하다고 가정한 그 f(x) 식의 게수로 대입해주는 것이다. y = f(x) 함수가 x = a 에서 무한번 미분가능하다는 조건이 만족되면, y = f(x) 함수를 x = a 근처의 구간에서만큼은, 아래의 다항식으로 근사할 수 있다.

• x=a 에서 위의 테일러 급수가 어느정도 구간까지 유효한지는 함수마다 다르다
• x = a 와 가까울수록, 원본 f(x) 와 테일러 급수에 의한 다항 근사식과의 오차가 줄어든다
• x = a 와 가까울수록 무한대까지 급수를 끌고 가지 않아도 오차가 없을 것이고
• 약간씩 멀어질수록 급수가 더 필요하다. 다항식의 차수가 높을수록 더 잘 근사한다.