[Paper] Asymmetric polynomial loss for multi-label classification

Abstract

기존 multi-label classification 의 문제점
1. BCE loss 는 최적화된 모델, 도메인에서만 동작하여 다양한 tasks 에서까지 높은 성능을 보이는 건 아님
2. negative, positive 사이의 불균형이 성능을 낮춤

따라서 이 논문은, 이러한 문제를 해결하기 위해 Asymmetric Polynomial Loss(APL)를 제안.

• Taylor expansion on BCE loss 를 수행
• polynomial fucntions 의 계수 개선
• decouple the gradient contribution from negative, positive sample (asymmetric focusing)
• 검증, 다항식의 계수가 asymmtric focusing hyperparameters 를 교정하는지

텍스트와 이미지 모두 검증한 결과 APL loss 가 성능 향상에 도움이 된다는 것을 밝힘.

[Multi-label classification, Taylor Expansion, Asymmetric Focusing, BCE]

1. Introduction

결국 목적은 더 다양한 tasks 에서도 동작할 수 있도록 loss function 을 tuned 한다는 것.
발견한 두가지 사항이 있다.

1. 각각의 동립적인 binary classfication 부문제에서, negative log-likelihood loss 는 최적이 아님 (lagarithm's Taylor expansion의 다항식 계수) -> 이것들을 합친 multi-label claasification 문제에서도 따라서 최적이 아님

2. 만약 positive label이 적고, negative label 이 많은 식으로 불균형하다면 문제 -> 많은 negative samples 들이 더 gradient weights 에 가담하여 positive samples 에 대해 최적이 될 수 없음

💡논문의 제안: 그럼 Asymmetric Polynomial Loss 라는 걸 쓰자 (APL).
추가로, 서로 다른 클래스 개수에 대한 문제를 없애도록 각각의 클래스에 대해 계수를 조정하는 것이 아니라 -> collectively tune the coefficients of leading polynomial

2의 문제를 해결하기 위해서 asymmetric focusing mechanism 사용, 드문 positive samples가 gradient contribution 을 늘리도록.

• Defferent focusing parameters가 loss 를 분리시키고,

• positive samples 에 집중

• easy negative samples (부정이라 판단되는 확률이 적은 것)의 방해를 줄이기 위해 계산시에 배제

• APL loss(from Talyor expansion: 다양한 tasks 에 더 잘 동작)

• APL 의 다항식 계수와, asymmetric focusing 사이의 파라미터 정교화

2. Methodology

✅ Taylor Expansion for BCE
BCE loss 는 C개의 독립적인 분류 부문제로 구성.

• positive class 에 대해 -log(p)
• negative class 에 대해 -log(1-p)
• p 는 시그모이드 함수를 지난 prediction probability

BCE loss 의 부문제들을 최적화하기 위해, Taylor series expansion 를 BCE Loss 에 적용.

🤔테일러 expansion 이 뭐지? -> 정리 참고

• y = 1인 positive class 에 대해선 expansion point 를 1로,
• y = 0인 negative class 에 대해서는 expansion point 를 0으로

➡️ -log(x) 를 expansion point 1로 하고 Taylor Series 로 나타낸 식은 다음과 같다.

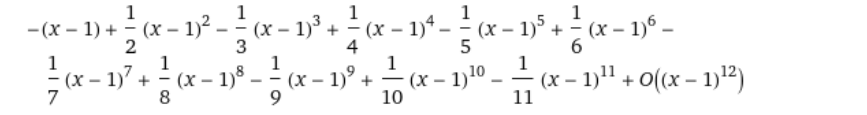
➡️ -log(1-x) 를 expansion point 0으로 하고 Taylor Series 로 나타내면 다음과 같다.

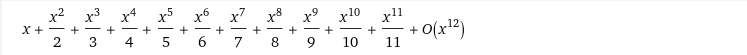
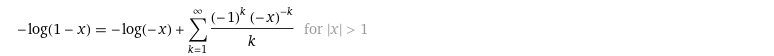
< T-BCE >

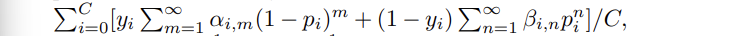
• log likelihood 부분이 m 1부터 무한대까지 1/m X (1-p)^m, n 1부터 무한대까지 1/n X (1-p)^n으로 바뀐 것임.
• 다항식 leading 계수를 바꾼 것은 이 계수 자체가 훈련 나중이 될 수록 영향력이 높아지기 때문이다.

✅ Asymmetric Polynomial Loss
샘플 자체의 불균형을 완화. loss +, - 에 따라 이 둘을 다루는 다른 scailing factors 감마 사용. -> 직접 positive, negative class 에 따른 gradient 비율을 조정할 수 있다. (다항식 지수에 적용, m+ 감마+ / m+ 감마-)

추가적으로 이렇게 비율을 조저아는 것 뿐만 아니라 작은 예측 확률을 가진 negative class 들은 버리는 방법을 이용했다.

• treshopd p_th 보다 작으면 loss 계산에서 버리는 방식 이용
  

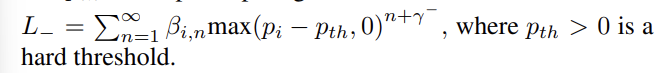
다항식 계수에 대한 조작은 collectively 하게.

➡️ 모두 합치면, APL은 다음과 같다.

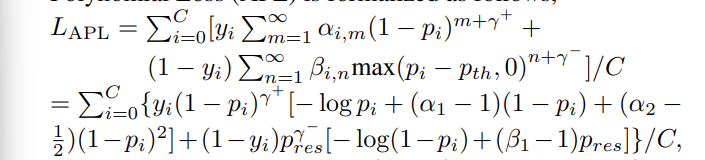
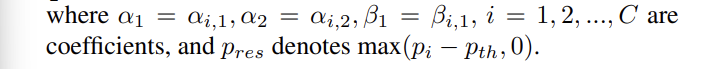
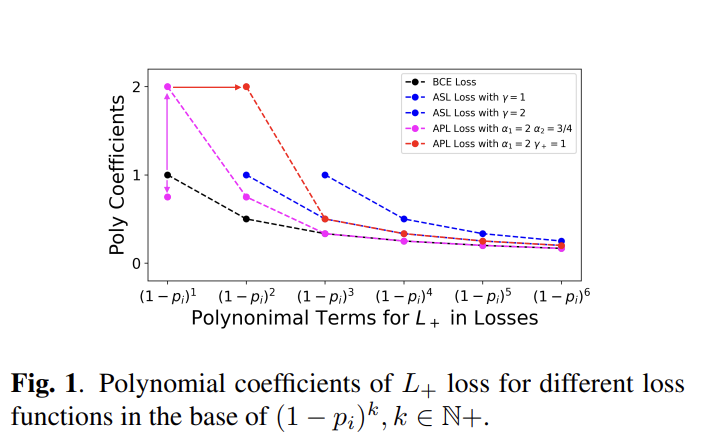
< Fig1 >

• BCE loss 의 고정된 계수에 반해 ASL loss 는 수직적으로 움직일 수 있고,
• APL loss 또한 수직, 수평의 조정을 가능하게 한다.
  

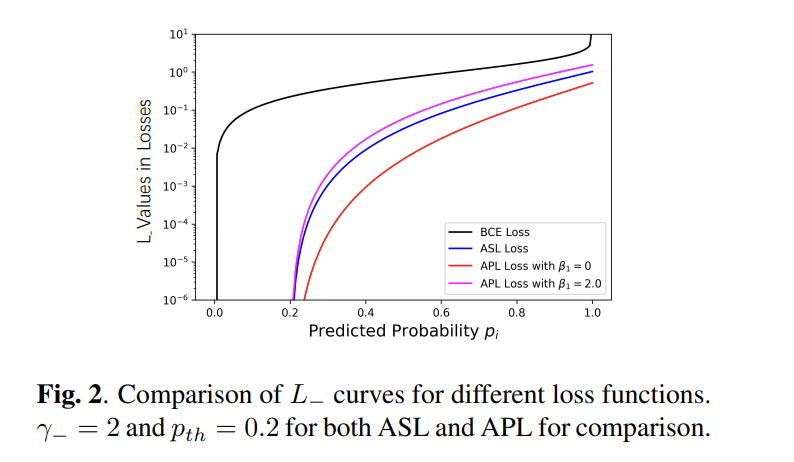
< Fig2 >

• treshold 밑의 샘플들은 제거하여 높은 확률에 기여
• 계수 베타를 조정하는 것은 positive, negative lass 의 비율을 조정하는데 도움
• mislabeling 문제를 해결
  

✅ Gradient Analysis
positive, negative 에 대한 gradients 를 분석해보자.

positive class는, 감마를 = 0 으로 설정할 때 gradient 는

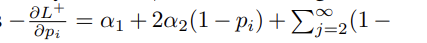
와 같다.

• 알파1은 p에 상관없이 지속적인 gradient 를 제공하고
• 알파2는 p와 linear correlation 을 제공한다.

negative class 의 경우

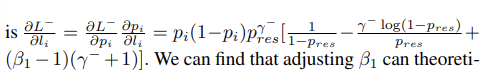
• 베타를 조정함으로써 mislabeling problem 해소 가능
  

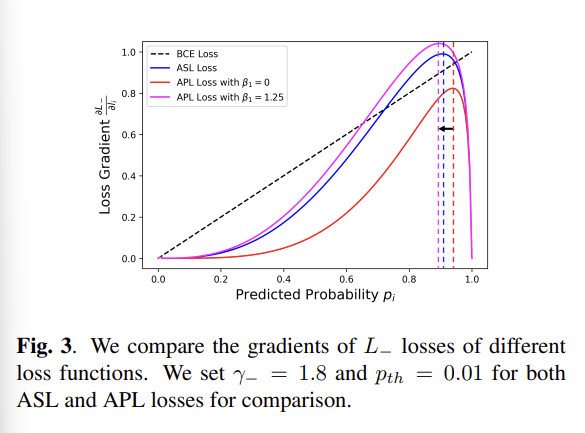
✅ Parameter Interaction Analysis