[NLP] Attention Mechanism

Attention 이전에 가장 주목받았던 알고리즘은 RNN을 포함한 Seq2Seq 모델이었다. 그런데 RNN의 고질적인 문제 때문에 이 모델에는 단점 두 개가 존재.

1. '하나의' 고정 크기 벡터에 모든 정보를 압축하려고 하니 정보 손실 발생

2. RNN 고질적인 문제인 기울기 소실 문제 존재

2가지의 문제 모두 긴 문장에 대한 처리를 어렵게했다. 이러한 문제를 타파하기 위해 등장한 것이 Attention 이며, 긴 문장에 대한 정확도를 어떻게 올릴 수 있었는지 확인하자.

Idea

어텐션의 기본 아이디어는 디코더, 즉 단어를 실제로 출력하는 예측을 진행할 때마다, 인코더의 '전체' 입력 문장을 다시 한 번 참고한다는 것이다. 이때 참고는 RNN 기반의 Seq2Seq 처럼 하나의 셀에 담긴 정보만 가져오는 것이 아니라 모든 단어를 살피며, 그 중에서도 예측해야할 단어 (t시점의 단어)와 연관이 있는 입력 단어에 집중해서 살피게 된다. 따라서

• 인코더로부터 집약된 하나의 셀이 아닌 전체 입력 문장에 담긴 토큰들을 모두 살피며
• 그 중에서도 예측할 단어와 연관이 있는 단어에 집중(Attention)한다!

Attention Function

어텐션 함수는 Qeury, Key, Value 세 가지를 통하여 계산되는데, 따라서 어텐션 함수를 이해하기 위해선 Q, K, V가 각각 무엇을 의미하는지 알아야 한다.

아래의 그림을 보자.

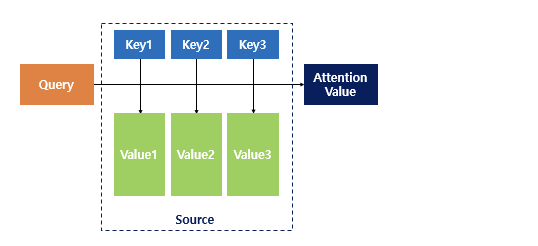
Key와 Value 는 우리가 흔히 파이썬 딕셔너리에서 알고 있는 키와 값과 같다. 그렇다면 Attention 에서 각각은 무엇을 의미할까?

Query: 구하고자 하는 값, t시점의 디코더 은닉 상태
Key: 모든 시점의 인코더 셀 은닉 상태들
Value: 모든 시점의 인코더 셀 은닉 상태들 (유사도 반영)

Key와 Value 모두 인코더 셀을 나타낸느 것은 맞으나 key는 단어 자체의 은닉 상태를 뜻하고, 쿼리에 대해서 모든 키와의 유사도를 구한 값이 Value 이다. 따라서 Value 를 구하기 위해선 키에 각각 쿼리와의 유사도를 계산해야 한다. 최종적으로 Attention Value 를 구하기 위해선 유사도가 반영된 Value 를 모두 더해서 리턴한다.

Dot-Product Attention

어텐션에는 다음과 같은 종류가 존재한다.

• dot
• scaled dot
• general
• concat
• location - base

먼저 전체적인 계산 흐름을 이해하기 위해 가장 쉬운 dot-product attention 을 이해해보자.

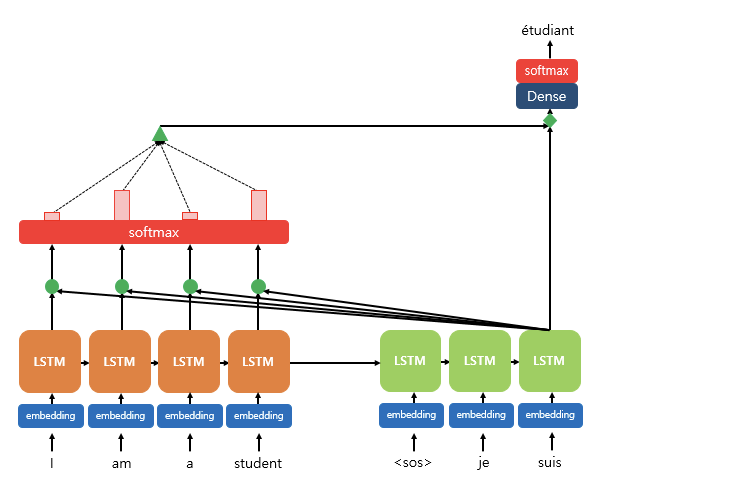
아래 그림은 디코더의 세번째 LSTM 셀에서 출력 단어를 예측할 때의 계산과정이 어떻게 이루어지는지를 나타낸 것이다.

• 디코더의 세번쨰 LSTM 셀은 출력 단어를 예측하기 위해서 인코더의 모든 입력 단어들의 정보를 다시 한번 참고한다
• 소프트맥스 적용 후 결과값은 I / am / a / student 각각이 얼마나 도움이 되는지 정도를 수치화한 값
• 예측에 도움이 되는 정도를 하나로 담아 디코더로 전송 (초록색 삼각형)
• 결과적으로 출력 단어를 더 정확하게 예측할 확률이 높아짐

순서대로 알아보자.

1. Attention Score 계산

• 인코더의 은닉 상태 $h_1, h_2, h_3 .. h_n$
• 현재 시점 디코더의 은닉 상태 $s_t$

현재 시점 t에서 예측을 위해 디코더에게 필요한 '입력값'은 이전 시점 t-1의 은닉 상태와 출력 단어, 그리고 Attention 에서 추가로 도입된 Attention Value 라는 새로운 값이다. 따라서 t번째 단어를 예측하기 위한 Attention Value 를 $a_t$라고 정의하자.

t-1 시점의 은닉 상태와 출력 단어, 그리고 $a_t$ 를 어떻게 계산하기 전에 $a_t$ 자체가 어떻게 계산되는지 살펴야 한다. 첫번째 순서는 attention score 를 계산하는 것이다.

Attention Score 란 현재 예측하려고 하는 t시점의 단어 은닉 상태 $s_t$
와 인코더의 각 은닉 상태 $h_n$ 이 얼마나 유사한지 판단하는 점수이다. 따라서 간단한 내적으로 이를 계산한다.

• $s_t$를 전치하고
• 인코더의 각 은닉 상태와 dot product
• n개의 attention score 값

$socre(s_t, h_i) = s_t^Th_i$

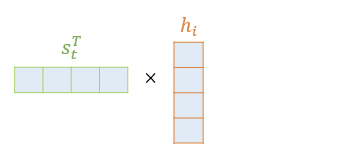
어텐션 스코어의 모음 값을 $e^t$ 라고하면

$e^t = [s_t^Th_1, s_t^Th_2, .. , s_t^Th_n]

2. Attention distribution 을 Softmax 를 통해 계산

각각의 구한 어텐션 스코어 = e^t에 소프트 맥스함수를 적용하면 모든 값을 합하면 1이 되는 확률 분포를 얻을 수 있다. 이를 Attention distribution 어텐션 분포라 하며, 각 값은 Attention Weight 어텐션 가중치라 한다.

아래의 그림에서 소프트맥스 적용 이후 빨간색 직사각형 크기가 각각의 어텐션 가중치를 나타낸다.

$\alpha^t = softmax(e^t)$

• $alpha^t$ 는 어텐션 분포
• $e^t$ 는 어텐션 score 모음 값

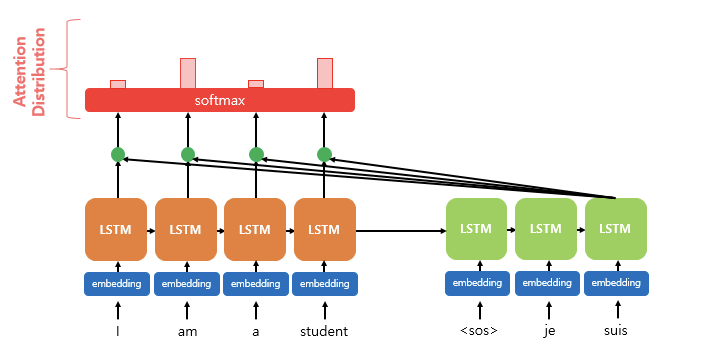
어텐션 스코어를 가중치로 변환시키는 이유는 유사도를 확률과 연관시키기 위함이다. 각 인코더 은닉 상태와의 연관도 숫자를 조금 더 정규화시킨다는 데 그 의미가 있다.

3. 인코더 어텐션 가중치와 인코더 은닉 상태를 가중합하여 Attention Value 계산

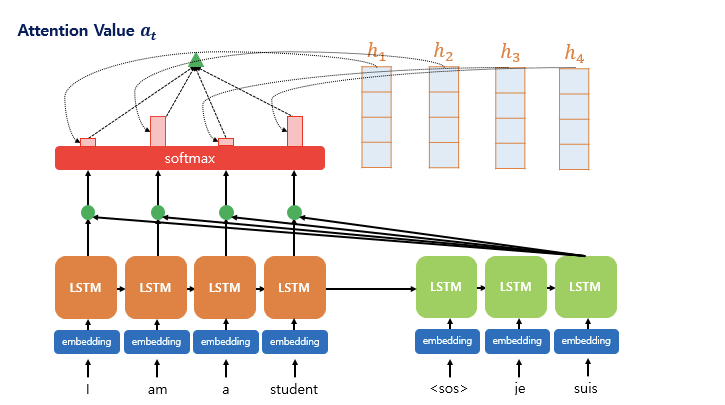
어텐션의 최종 결과값을 얻기 위해 인코더의 은닉 상태와 어텐션 가중치값들을 곱한다. 무슨 의미일까?

• 인코더 은닉 상태는 예측하려는 단어와 관계없이 그 단어의 문맥을 학습한 값이다
• 어텐션 가중치는 인코더 그 단어와 예측하려고 하는 단어와의 유사도를 확률로 나타낸 값이다. (얼마나 중요한지)

따라서 두 값을 곱하면 실질적으로 예측하려고 하는 단어와 유사도를 반영한 그 단어의 문맥 정보를 구한 값이 된다. 이를 Weighted Sum 하면 어텐션 값 Attention value $a_t$ 를 계산할 수 있다.

$a_t = \sum \alpha_t^th_i$

• $a_t$ 는 attention value 로 예측하려고 하는 디코더의 값과의 유사도를 반영한 인코더의 문맥이다 => Context vector

따라서 중요하게 보아야 할 것이 인코더의 마지막 은닉 상태를 단순히 Context vector 이라 부르는 것과 대조된다. (멀고 가까운 것이 계산에 반영되지 않는다.)

4. Attention 값과 t시점의 은닉 상태 Concatenate

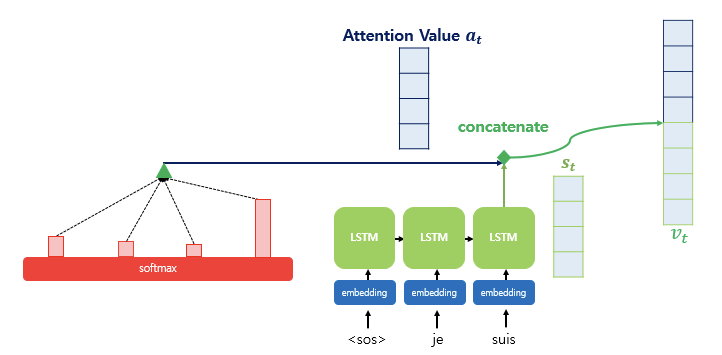
어텐션 함수의 값인 $a_t$ 를 구했으므로 디코더 t시점의 은닉 상태와 Concat한다. 디코더 t시점 은닉 상태는 $s_t$로, 아까 처음에 인코더의 각 은닉 상태 $h_i$와 dot product 할 때 사용했던 바로 그것이다! 그 단계에선 유사도를 구해 attention score 를 구하기 위해, 지금 단계에선 하나로 모아진 문맥 정보와 은닉 상태를 연결하기 위해 가져온다.

$a_t$ 와 $s_t$ 를 Concat 하여 하나의 벡터로 만든 것을 $v_t$ 라 하며, 예측 연산의 입력으로 사용한다.

5. 출력층 연산의 입력이 되는 $s_t$ 를 계산

마지막으로 $v_t$를 바로 출력으로 사용하기 보다 신경망 연산을 한 번 더 추가한다

• $v_t$를 가중치 행렬 W와 곱한 다음
• tanh 함수를 지나여
• 새로운 벡터인 $\tilde{s}$ 를 계산한다.

$\tilde{s_t} = tanh(W_c[a_t; s_t] + b_c)$

• W는 학습 가능한 가중치 행렬이며
• b는 편향

6. $\tilde{s_t}$ 를 출력층의 입력으로 사용

• 가중치 행렬과 한 번 곱하고
• 편향을 더한 후
• Softmax 를 거치는 신경망 연산을 한 번 더 거친 후
  예측 벡터를 얻는다

$\hat{y_t} = Softmax(W_y\tilde{s_t} + b_y)$

다음은 바다나우 Attention 에 대해 알아보자.

Reference

https://wikidocs.net/22893