[Paper] Locating and Editing Factual Associations in GPT

Locating and Editing Factual Associations in GPT

• reason to read: knowledge editing field paper but applies similar techniques in interpretability of LLM, what is the rigorous mechanism for storing and recall of factual associations in LM? How can it be edited?
• Link: https://arxiv.org/pdf/2202.05262

• Autoregressive 모델에서의 fact associations storage, recall 에 대해 분석한 논문
• neuron activation 분석 위해 causal intervention
• 그 중에서도 middle-layer feed-foward 가 fact 를 처리하는 곳이라 보고, 이를 검증.
• 지식 editing 을 위해 Rank-One Model editing (ROME) 도입, 효과적인 model editing 임을 입증.

1. Intro

이 논문은, factual association 을 모델에서 어떻게 저장하는지, recall 하는지 파악하기 위한 논문. 먼저 어떤 module 이 주어진 '주어'에 대한 fact 를 recall 하는지 파악하기 위해 hidden state activation 을 조사 (causal mediation analysis) . 그리고 여기서 모델의 middel layer mlp 가 가장 이 정보를 처리하는데 있어 핵심적인 곳이라 봄. 그 다음으론, 이를 검증하기 위해 Rank-One Model Editing 으로 weights 를 건드려서 과연 이 레이어가 담당하는 것인지 확인.

결론적으론 'midlayr MLE modules' 가 팩트연관을 저장하는 localized 된 곳임을 확인함. 또한, 다른 model editing 방법과 비교해서 ROME 이 generalization, specificity 를 동시에 달성할 수 있는 좋은 방법임을 보임.

2. Intervntions on Activations for Tracing Information FLow

이 절에선 hidden state 에 대한 분석, hidden state 가 이미 알려진 트랜스포머 구조에서 정보 처리 하는 것을 formal 하게 표현해내려고 노력함.

• fact as a knowledge tupe t = (s, r, o); 주어, relation, 목적어로 구성.
• (s, r) 과 함께 프롬프트를 줘서 o를 평가하면 모델이 주어에 대해 어떤 지식을 가지고 있는지 확인하는 것이 가능.
• 주어진 토큰 시퀀스가 들어오면, 모델은 이를 임베딩 벡터 + position encoding 을 더해 hidden state (0)번에 전달.
• final output 은 마지막 레이어의 token number T에 대한 hidden state 임.
• 아래와 같이 formal 하게 표현.

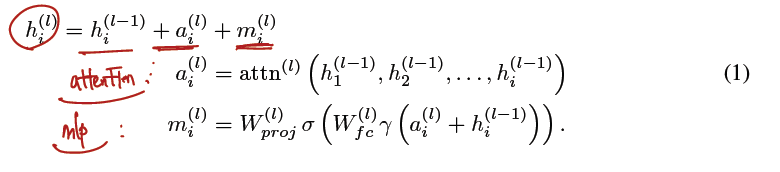
• 각 MLE layer 는 2개로 구성되어 있으며 fully connected, projection matrics 가 됨.
• 비선형성 추가.

이제 위 그림을 보면서 Causal Tracing 에 대해 좀 알아보자.

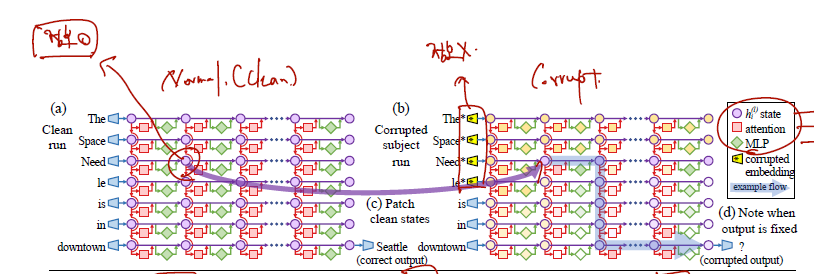
• grid of states 가 causal graph 를 형성한다고 가정.
• 여기에 recalling a fact 하는데 중요한 hidden state 를 찾기 위해..
• 1. clean run. "The Space Needle is in downtown ___ " 이란 문장을 주고, "Seattle" 로 예측하기 위해 모델이 동작하는 모든 ${h_i^(1)}$ 들을 얻음.
• 2. corrupted run. 위 문장에서 주어 entity 의 임베딩을 구할 때, 기존 임베딩에 정규분포를 따르는 epsilon 을 더한 노이즈가 있는 임베딩을 주게 됨. 그리고 이때 예측을 위해 모델이 동작하는 모든 ${h_{i*}^(1)}$ 를 얻음. 따라서 ${h_{i*}^(1)}$ 는 예측을 하는데 충분한 정보가 포함되지 않은 state 들일 것임.
• 3. corrupted with resoration run. 2번 정보를 잃은 상태에서 동작시키되 어떤 hidden state 가 중요한지 밝혀내기 위해 1 clean run 에서의 state 을 하나씩 불러와서 결과를 보게 됨.

따라서 각각의 run 을 하면 o가 나올 확률을 1. clean, 2. corrupted, 3. corrupted with resoration 에서 구할 수 있고.. 다음과 같이 notation

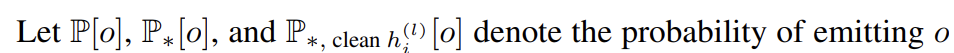
순서대로 1 > 3 > 2 순으로 확률이 높을 것이므로 다음과 같이 지표를 설정한다.

1. total effet (TE) := 1 - 2
2. Indirect effect (IE) := 3 - 2

이 둘을 여러 샘플에 대해 평균 내면, 각 hidden state 에 대해 average total effect (ATE) 와 averge indirect effect (AIE)가 계산된다.

Causal Tracing Results

• 1000 문장에 대해 AIE 평가.
• 해서 hidden state 뿐 아니라 각 l layer i 토큰에서 요소들 (state, MLP, attention) 을 restoring 하고 AIE 를 점수내면 다음과 같다.

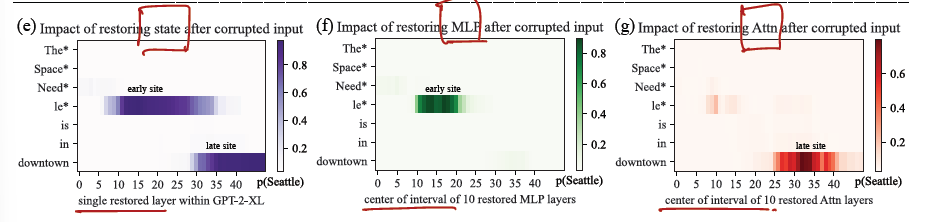
(Findings)

• late site 에서는 예측 시 중요하다는 건 알고 있었지만, early site, 특히나 주어의 마지막 토큰이 중요하다는 건 non-trivial fact 다.
• 그리고 early site 에서 보다 중요한 역할을 하는 건 MLP다.
• 각 layer 에서 AIE 의 그림을 그래프로도 나타냈다. (이건 기존 single state 만 데려온 것과 반대의 개념이니 주의)

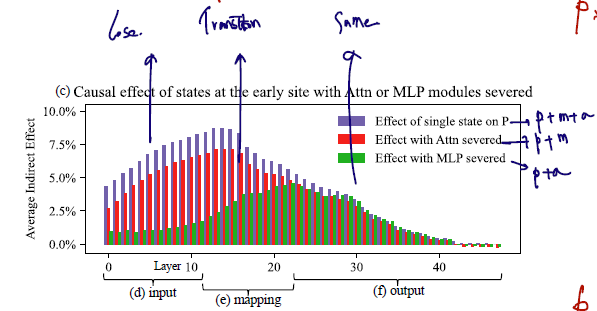
• 보라: single state p 로만 예측한 경우. (각 state 에는 attention과 MLE 가 모두 가담되어있다고 보는 것이 맞음.)
• 빨강: attention 이 serve 된 경우. 그러나 이때의 attention 은 corrupted input condition 에서 얻은 것을 교체한 것이므로 single state + mlp 정보 유지 + 해당 레이어의 attention 정보 삭제로 보는 것이 맞다.
• 초록: corrupted input 에서 얻은 mlp serve 가 된 경우이므로, single state + attention 정보를 유지 + 해당 레이어의 mlp 정보 삭제했다고 보는 것이 맞다.
• 앞쪽 레이어에서 보라, 빨강에 비해 초록에서 lose 가 크다는 건 주로 mlp가 해주던 역할이 컸다는 이야기이고..
• 저자들은 이를 input - mapping - output 단계로 나누어 input 에선 큰 lose 가 보이고 output 에선 차이가 안나는 이유로 중간 단계, mlp mid layer 가 중요한 역할을 해줬던 것이라고 분석.

따라서 다음과 같이 가설을 설정함.

• 각 midlayer MLP modul 은 주어의 마지막 위치에서 이를 인코드하는 정보를 받아들이고,
• 주어에 대한 기억을 recall 하는 output 을 생성.
• 그러면 attention at high layer 에서 이를 카피.

위 가설을 testing 하기 위해 ROME 으로 넘어간다.

3. Interventions on Weights for Understanding Factual Association Storage

MLP layer 역할에서 fully-connected layer는 key, projection layer 는 value 라고 지정. (이미 MLP 가 k-v 로 매핑된다는 다른 논문 있었음.)

Rank-One Model Editing 방법은 새로운 지식을 삽입하는 방법이다. 따라서, 새로운 지식을 t = (s, r, o) 로 표기하고 현재의 tuple 은 o에 ^c를 달아 표기한다.

우선 ROME 은 새로운 k,v 를 insert 하기 위해 다음과 같은 closed form 문제에 대한 해를 찾게 된다.

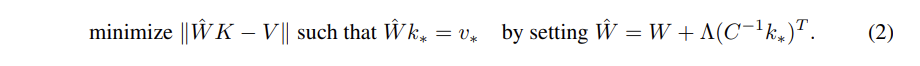
• W hat 은 기존 W에서 새로운 key-value 쌍에 대한 error 가 추가된 새로운 W matrics 임.
• 그 W hat 변경된 W에 대해 value 가 나오도록 (o가 나오도록) 값들을 최적화하는 문제를 푼다는 것인데,
• 새로운 k, v 값들은 어떻게 얻을까?
  

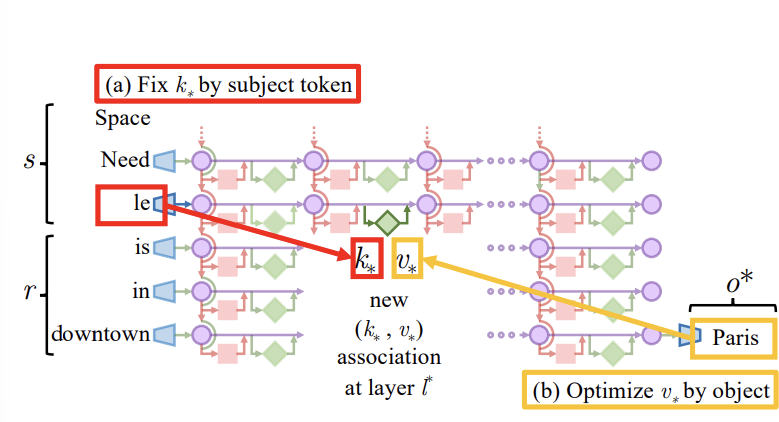
Step 1: Choosing k∗ to Select the Subject.
k* 값은 '주어의 정보를 잡아내는 k값'을 얻는 게 포인트다.

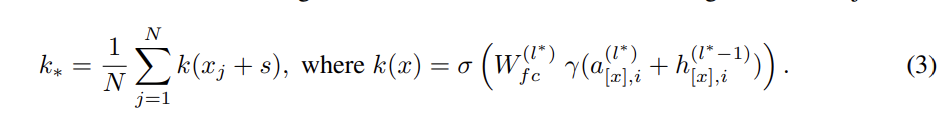
• s는 변경하고 싶은 fact 가 있는 주어이고, xj 는 이 앞에 random sequence 를 갖다 붙인 것.
• 그러고 나서 run 하여 i번째 토큰에 있는 mlp layer 의 key 값을 얻는 과정을 여러번 반복해서 평균 내게 된다.
• 따라서 k* 는 주어 subject 의 정보를 잡아내고 실제로 key 가 '잘' 될 수 있는 vector 가 될 것이고..

Step 2: Choosing v∗ to Recall the Fact.
v 값은 주어의 key 값이 들어올 때, 바꾸고 싶은 내용 o 가 최대한 나오도록 하는 mlp output 이 될 것이다. 따라서 다음 L(z) 식의 최소화원 z가 v* 가 된다.

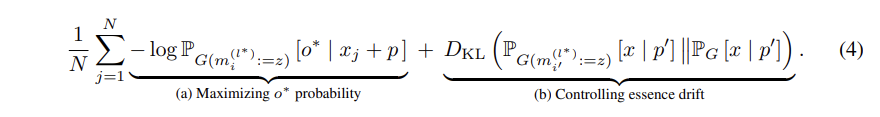
• 주어진 L(z) 해석: 주어의 마지막 토큰 i번째 위치에서 mlp output z들이 있을 때, o* 이 나올 확률이 최대가 되도록 함.
• L(z)의 최솨화원을 v 로 한다는 것: v 는 mlp output z 중에서 o 이 나올 확률이 가장 크도록 하는 z가 v 로 선택됨.

Step 3: Inserting the fact

(k, v) 로 갈아끼우고 (s, r, o*) 가 나오는지 테스트.

• efficacy 는 주어진 s, r, o* 과 s, r, o^c 를 비교하고
• generalization 은 s, r 을 똑같이 하고 prompts 만 rephrased 하여 측정
• specificity 는 s 에 대한 fact 를 바꿨을 때 주위의 sn 이 수정되진 않는지 체크. (수정되면 bad.) 따라서 p(o^c) > p(o*) 를 성공 event 로 간주.

ROME Results

(1)

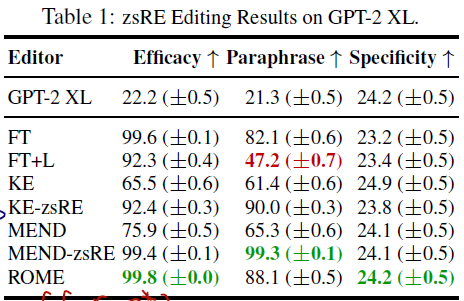
(2) 주어진 o* 가 나올 확률에서 o^c 가 나올 확률의 차 (S), 비율 (M).

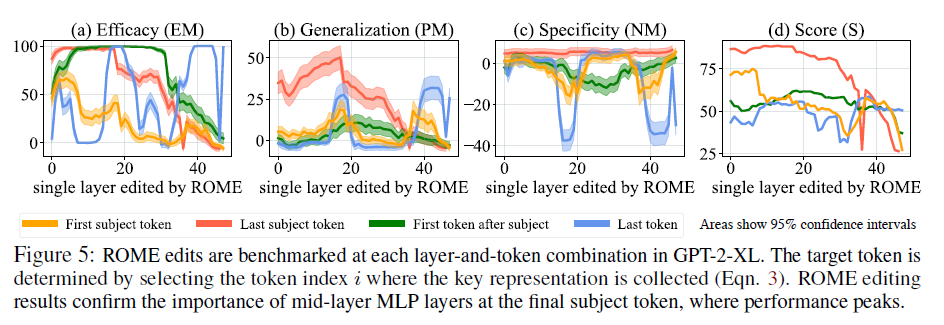
• generalization 이나 specificity 나 last subject token 에서 최대가 됨.