# ml06

The alignment problem

• lack of helpfulness
• Hallucinations
• Lack of interpretability
• Generating biased or toxic output

RLHF (Human Feedback based Reinforcement Learning)

applied to ChatGPT three main steps: pre-training, fine-tuning, interaction with humans.

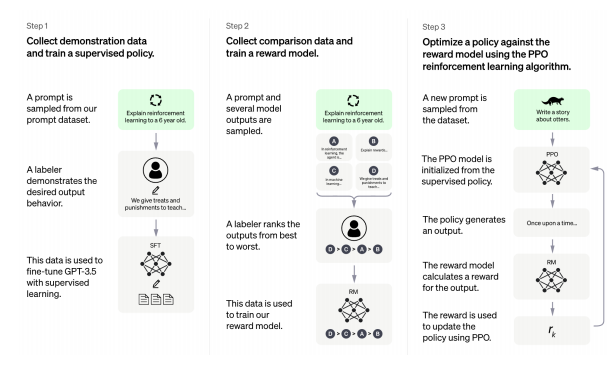
하나의 질문에 적절한 정답 여러개를 제시하면, 그 중에서 순위를 매기고, 이러한 데이터는 reward model 로 사용.

인간 피드백은 Reward predictor 을 만드는데 사용된다. 이를 가지고 reward 를 예측하면 RL algorithm 이 완성된다.

1. Pretraining LM (STF)

2. Training a reward model. (5점 만점 rating 을 하거나 0/1)

3. Fine-tunign the LM with RL
   

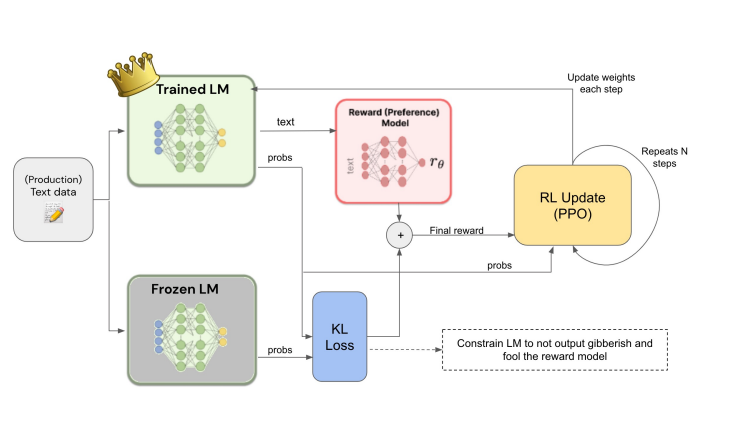
• 처음으로 만든 LM 은 Frozen
• old policy/ new plicy 를 가지고 loss 를 계산하여, 가중치를 업데이트 하면서 Trained LM 을 만든다.

PPO

어떤 상황에서 써야할까?: sequential decision making 을 해결하고 싶을 때.

• Environment: Markov Decision Process(MDP) 로 Agent 을 둘러싼 보든 정보들을 정리
  
• Policy: Agent 가 선택할 행동, 확률 $\pi(a|s)$
• Reward: Agnet 의 상태나 행동이 얼마나 좋은지 알려주는 정보
• Objectives: 미래의 보상의 합이 최대화되는 정책을 찾기; Optimal Policy

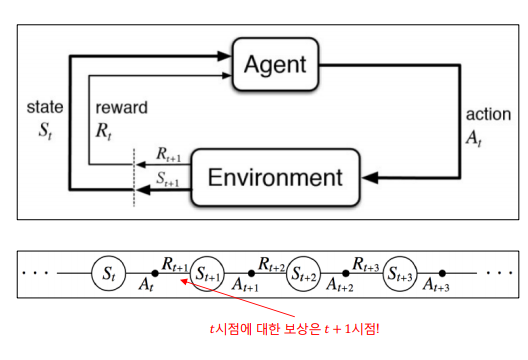
• $S_t$: 에이전트가 t 시점에 존재하는 어떤 상태
• $A_t$: 에이전트가 t 시점의 상태에서 하는 행동
• $R_t$: 에이전트가 t-1 시점의 상태에서 한 행동에 대해 t 시점에 환경이 주는 보상

Markov Decision Process

• Markov property: 미래는 오로지 바로 이전 현재에 의해 결정된다. (St+1 을 계산하려면 St만 있으면 충분하고 그 이전 상태인 S1, S2, S3 는 영향을 주지 못함)

• Markov Process MP = (S, P)

• 이때 S는 상태집합을 뜻하며, 가능한 상태들을 모두 모아놓은 집합이다.

• P는 상태 s에서 상태 s'에 도착할 확률을 뜻한다.

• 전이 학률 행렬은 다음과 같다.
  

• Markov Reward Process: MRP = (S, P, R, r)
• 상태 집합 S
• 전이확률 행렬 P
• 보상함수 R(어떤 상태 s에 도달했을 때 받게 되는 보상)
  
• 감쇠인자 감마는 0에서 1사이의 숫자로 미래의 보상과 현재 보상 중 어떤 것을 중요시할 것인지에 대한 가중치이다.
  

• episode: s0에서 st까지 가는 여정
• return: t시점부터 미래에 받을 감쇠된 보상의 합을 뜻한다. 이 리턴을 최대화하도록 학습!
  

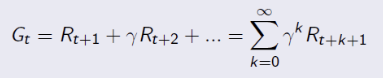
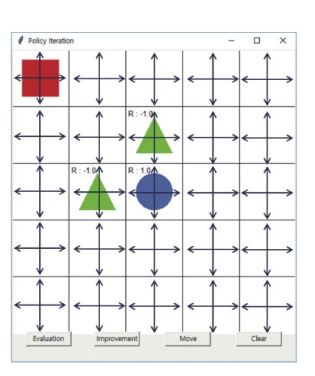
Markov Decision Process(MDP): 실제 action 을 적용!

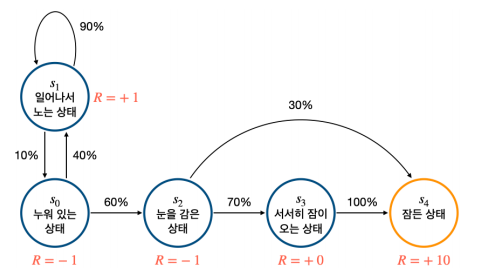
• S: 각 상태를 위치로 정의할 수 있다.
• A: up, down, left, right
• R: 세모= -1, 동그라미 = +1
• 상태전이확률: 1로 정의
• 할인율 감마: 0.9
• 정책 $\pi(a|s)$: 0.25 로 정의
  

가치함수 (Value function)이란 현재 상태가 얼마나 좋은지 Estimate 한 값을 말한다. 가치함수는 상태에 대해 미래 보상에 대한 기댓갓으로 정의한다. 두가지 가치함수를 보자.

상태가치함수(State-value function): the expected return starting from stat s, and then following policy $\pi$

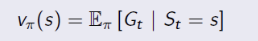
행동가치함수(Action-value function, Q-function): the expected return startin from state s, taking action a, and then following policy $\pi$

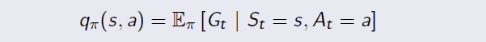
Bellman Expectation Equation

s 상태에서는 a1 행동 또는 a2 행동을 취한다. a1을 취하면 q(s, a1), a2를 취하면 q(s, a2) 로 표현할 수 있고, 상태가치함수는 확률에 Q함수를 곱한 값이다. (가치함수와 Q함수의 관계)

q(s, a)는 어떻게 계산할까? a1를 고른 상태에서 s'1 과 s'2 로 갈 수 있다고 했을 때, s'1으로 갔을 때의 보상과 s'2 로 갔을 때의 보상과 상태 변환 확률을 더한다. (보상과 상태 변환 확률에 따른 다음 상태)

이를 종합하면 현재 상태의 가치함수 <> 다음 상태의 가치함수의 관계를 구할 수 있다.

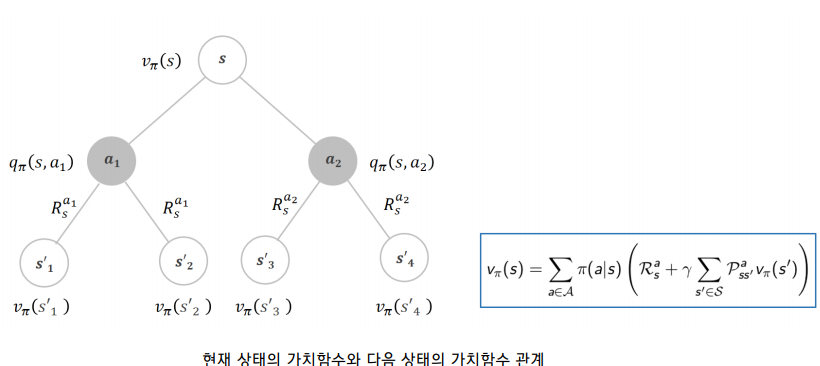
action의 가짓수에 따라 모든 v를 계산한 다음 단순히 더하면 Expectation, 기대가치함수를 구할 수 있다.

그러나 구할 수 있는 Q함수 중 가장 큰 값을 구하는 것이 Bellman Optimality Equation 이다. 이때는 DP를 사용한다.

• Bellman Expectation Equation => Policy interation
• Bellman Optimiality Equation => Value iteration

Policy Iteration

Value 평가하기 - 반복적 정책 평가

• 테이블 초기화
• 한 상태의 값을 업데이트
  
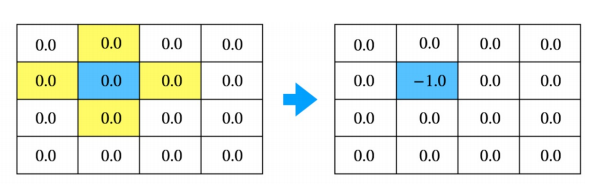
• 모든 상태에 대해 2 적용
• 2,3 을 계속 반복.
  
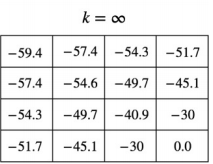
• 그리디 정책: 다음 칸의 가치가 큰 것을 선택한다.

Value Iteration

• 동, 서, 남, 북 네가지 액션에 대한 최댓값을 사용한ㄷ
• 모든 상태 s에 대해 벨만 최적 방정식을 이용해 업데이트
• 무한대 결과
  

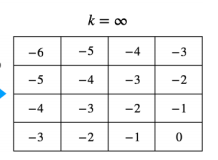
MDP 모를 때 밸류 평가하기

앞의 계산은 단순히 주어진 값으로 Iteration 계산에 그치는 것이지 기계학습이라 할 수 없다. (Planning) 따라서 Model-Free RL 이 필요하며, MDP에서 2가지 정보(보상, 전이확률)을 모를 때 MDP를 학습하는 것을 말한다.

정리하면 Dynamic Programming 은 MDP를 계산하고(Iteration), RL은 MDP를 학습한다. (MC, TD, SARSA, Q-Learning)

• Monte Carlo Method
  몬테 카를로 방법이란 에피소드 경험으로부터 직접 학습하는 것이며, 완료된 에피소드마다 가치함수를 업데이트한다. 경험하면서 반환값 Return Gt를 모으고, Sampling. 반환값의 평균을 통해 v(s)를 추정한다.

업데이트 식을 보자.

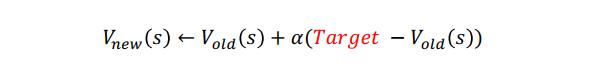
얼마나 가치함수를 업데이트냐 할 것인지를 뜻하며, Target 에서 기존 가치함수를 뺀 값 error 에 lr을 곱한만큼 업데이트한다. 이때 Target 은 에피소드가 끝나면 지나온 각 상태가치 함수를 업데이트한다.